Практическое занятие по Информатике. Карла информатика. Закон Кулона для взаимодействия точечных зарядов или заряженныхшариков в вакууме записывается в форме
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА НОМЕР 2 - Ms Word. Вставка формул Цель работы: освоить технологию вставки формул в текстовый документ C помощью приложения Microsoft Equation 3.0 Задание 1. Используя редактор формул Microsoft Equation 3.0, набрать следующий текст: Закон Кулона для взаимодействия точечных зарядов или заряженныхшариков в вакууме записывается в форме 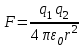 где 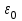 -электрическая постоянная в СИ. -электрическая постоянная в СИ.Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов Принцип наложения (суперпозиции) электрических полей:напряженностьэлектрического поля системы N зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:  где N – произвольное положительное целое число. Абсолютная величина |а| действительного числа а по определению есть число, равное а, если 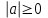 , или равное –а, если а меньше 0. , или равное –а, если а меньше 0.Отметим 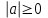 из из 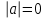 следует следует 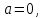  Задание 2. Используя редактор формул Microsoft Equation 3.0, набрать следующий текст: 1.Элементарные примеры раскрытия неопределенностей разного вида. Предел отношения двух многочленов с постоянными коэффициентам. При 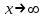 отношение многочленов представляет неопределенность вида. Для ее раскрытия преобразуем каждый многочлен, вынося за скобки переменную в наибольшей степени: отношение многочленов представляет неопределенность вида. Для ее раскрытия преобразуем каждый многочлен, вынося за скобки переменную в наибольшей степени: Таким образом, можно сформулировать следующие правила: Предел отношения двух многочленов одинаковой степени равен отношению коэффициентов при старшей степени; Если степень многочлена стоящего в числителе, больше степени многочлена, стоящего в знаменателе, то предел их отношения равен бесконечности; Если степень многочлена, стоящего в знаменателе, выше степени многочлена, стоящего в числителе, то предел их отношений равен нулю. 2.Найти наибольшее значение функции 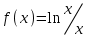 в интервале в интервале 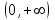 . .Решение. Всюду в интервале 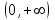 .функция дифференцируем. Найдем .функция дифференцируем. Найдем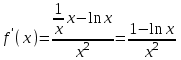 так как так как 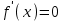 при при 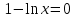 , то , то 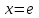 Задание 3. Используя редактор формул Microsoft Equation 3.0, набрать следующий текст: Метод Крамера решения системы n линейных уравнений с n неизвестными. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными: 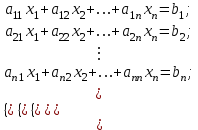 Определителем системы называется определитель матрицы системы 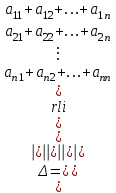 Обозначим 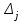 - определитель, который получится из определителя системы - определитель, который получится из определителя системы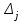 заменой j-го столбец заменой j-го столбец 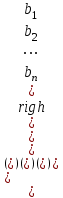 . .ЛАБОРАТОРНАЯ РАБОТА НОМЕР 3 Лабораторная работа MS Word. Создание, редактирование и форматирование таблицы Цель работы: научиться создавать таблицу; редактировать и форматировать таблицу; заполнять таблицу текстом. Используя команды для работы с таблицей, создать таблицу по образцу, заполнить ячейки таблицы и выполнить соответствующее форматирование, используя команды вкладки Главная, и вкладок для работы с таблицами Конструктор и Макет. Задание 1 Таблица 1- Результаты аттестации 2-го курса
Задание 2 Таблица 2 - Выборочные данные по факультету, 2007 г.
Задание 3 Таблица 3 - Данные по кафедре
Задание 4 Таблица 4 - Финансовый план предприятия на квартал
ЛАБОРАТОРНАЯ РАБОТА НОМЕР 6 Используя автозаполнение (по строкам и по столбцам) и ограниченное преподавателем время создайте нижеследующий документ и сохраните его в файле Автозаполнение.xls. Добейтесь того, чтобы данные в столбце М были не текстового, а числового типа. 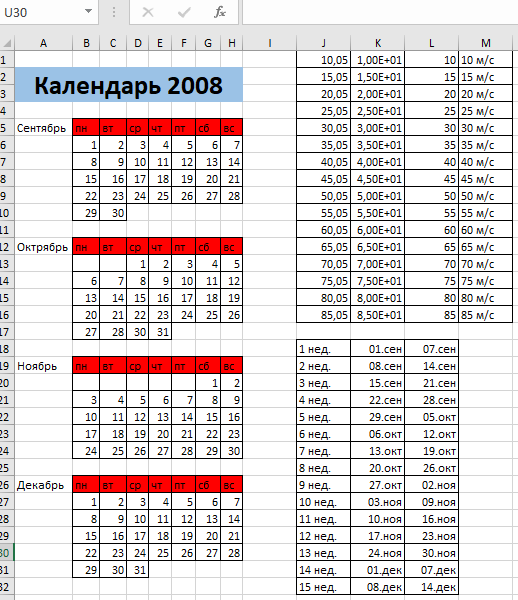 Имя ячейки выделенной в теле приведенного документа Q30. Форматы данных которые я использовал: в данной задаче я использовал данные различного типа. Практическая работа №2. Форматирование ячеек Создайте список группы учащихся и их успеваемости, отформатированный как показано ниже, и, используя условное форматирование, выделите двойки. Рассчитайте средний бал в отдельном столбце и определите отличников (4,6 < средний бал < 5.0), хорошистов (3,6 < средний бал < 4.5) и незнаек (2 < средний бал < 3.5) с помощью различных подсветок.. Результат сохраните в файле Форматирование.xls.
ЛАБОРАТОРНАЯ РАБОТА НОМЕР 8: Логические функции MS Excel Цель работы: изучить функции из категории Логические и их синтаксис; научиться записывать условия в Excel с помощью неравенств и с помощью логических функций НЕ, И, ИЛИ; изучить работу встроенного в Excel средства «Мастер функций» на примере функции ЕСЛИ; научиться вычислять выражения, зависящие от простых и сложных условий; рассмотреть применение логических функций к решению числовых и нечисловых задач. ИСТИНА'>ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ЛОГИЧЕСКИЕ ФУНКЦИИ 1.1. ОСНОВНЫЕ ПОНЯТИЯ Логическое выражение - это высказывание, принимающее значения ИСТИНА или ЛОЖЬ. Логические выражения в Excel позволяют выполнять вычисления, зависящие от условий. Условие считается выполненным, если значение соответствующего ему логического выражения - ИСТИНА, и не выполненным, если значение логического выражения - ЛОЖЬ. Логическое выражение может содержать знаки равенств и неравенств и логические функции. Равенства и неравенства применяются к двум операндам (сравниваются две величины). 1.2. ЛОГИЧЕСКИЕ ФУНКЦИИ ЕСЛИ, И, ИЛИ, НЕ Логическая функция ЕСЛИ имеет вид: ЕСЛИ(x1; x2; x3), где x1, x2, x3 – аргументы, здесь x1 - логическое выражение, x2, x3 – любые выражения, разрешенные в Excel; причем вычисляется x2, если x1 имеет значение ИСТИНА, и x3, если x1 имеет значение ЛОЖЬ. Если третий аргумент функции не определен, то ошибки в записи функции нет – в этом случае ей присваивается значение ЛОЖЬ, если условие не выполнено. Если ничего не нужно вычислять при невыполнении условия, следует в качестве третьего аргумента задать пробел как текст. Примеры: ЕСЛИ(A5>0;LN(A5);-1); ЕСЛИ(B2< >0;1/B2;” ”) Логическая функция И имеет вид: - И(x1; x2;; …;xn), где x1; x2;; …;xn – аргументы, являющиеся логическими выражениями. Функция может содержать до 30 аргументов. Функция И принимает значение ИСТИНА, если все ее аргументы истинны, в противном случае она принимает значение ЛОЖЬ. Функция может применяться для задания сложного условия, определяемого системой равенств и неравенств: x1 x2 ... xn x1 -истинно? x2 -истинно? или, в форме логических высказываний, ... xn -истинно?, 8 ВАРИАНТ ЗАДАНИЙ Задача 1. Вычислить указанные величины, зависящие от условий, с помощью логических функций. Параметр а задать самостоятельно. Исходные данные подобрать самостоятельно. Вычисления провести минимум для двух точек. 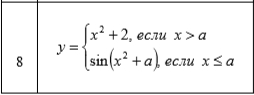   Задача 2. Вычислить указанные величины, зависящие от условий, с помощью логических функций. Исходные данные подобрать самостоятельно. Вычисления провести минимум для трех точек. 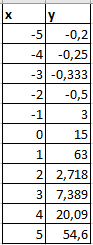 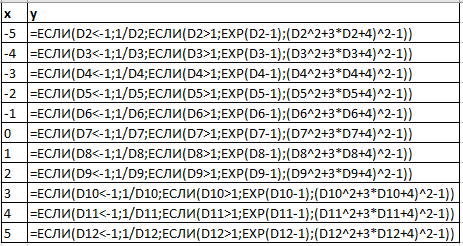 Задача 3. Определить принадлежность точек M 1 , M 2 , M 3 , M 4 , M 5 заданной области D. Область задана системами или совокупностями неравенств. Координаты точек на плоскости задать самостоятельно. 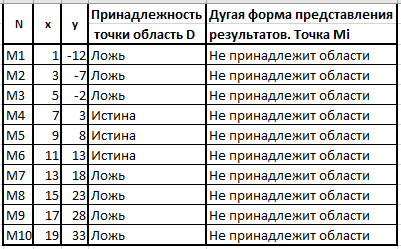 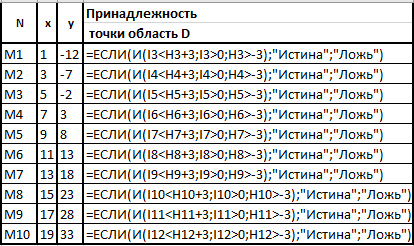 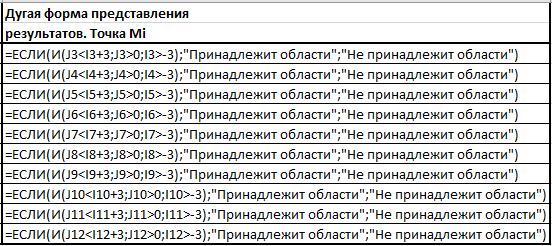 ЛАБОРАТОРНАЯ РАБОТА НОМЕР 9: Построение графиков функций Цель работы: Изучение графических возможностей пакета MS Excel. Приобретение навыков построения графика функции на плоскости средствами пакета. Задание 4.1. Вариант 8. Построить график функции f(x): 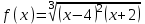 . .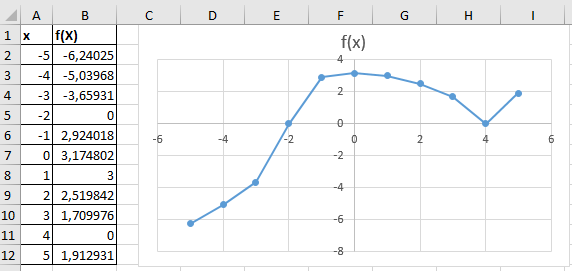 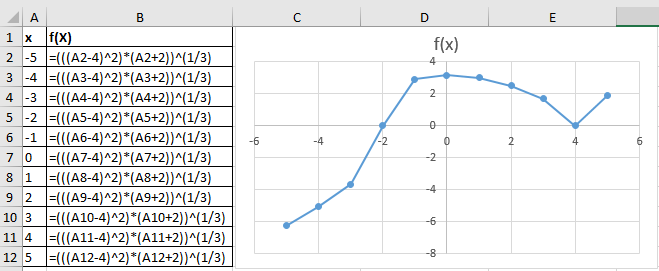 Задание 4.2. Построить график функции f(x). 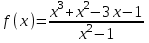 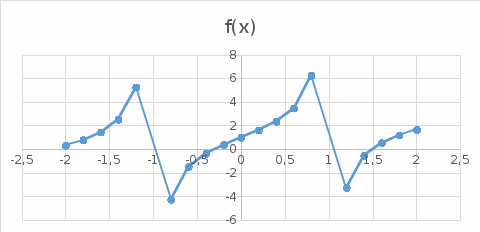 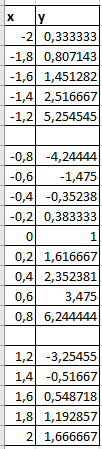 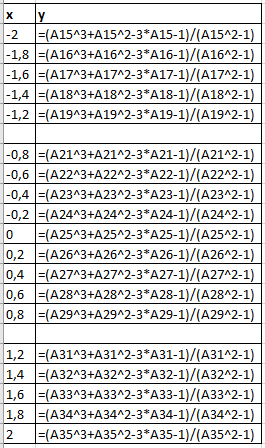 Задание 4.3. Построить график функции f(x): 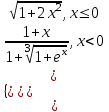   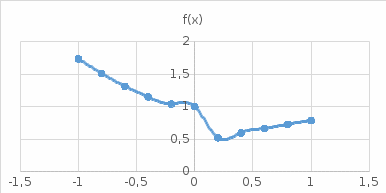 Задание 4.4. Изобразите линии заданные неявно уравнением f(x,y)=0. 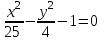 ; ; 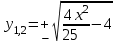 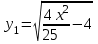 и и    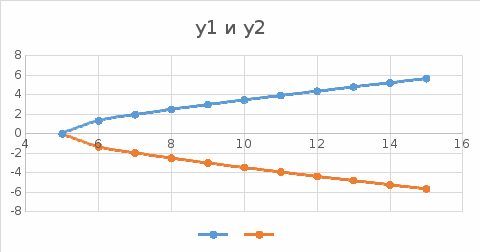 ЛАБОРАТОРНАЯ РАБОТА НОМЕР 10: Тема: “Использование массивов и табличных формул” Цель работы: изучить принцип работы с массивами и табличными функциями, ознакомиться с некоторыми встроенными функциями, которые используются для обработки матриц, закрепить на практике полученные знания. Задание 1. На первом листе книги Еxcel выполнить четыре учебных примера. Книгу сохранить.  Задание 2. На Листе 4 рабочей книги вычислить матричное выражение (вариант взять из таблицы 1). Числовые значения задать самостоятельно, оформить исходные данные, промежуточные результаты, конечный результат. Проверить аналитически результаты вычислений.   На Листе 5 рабочей книги решить систему линейных уравнений в матричной форме и методом Крамера. Проверить полученный результат подстановкой. Исходные данные взять из таблицы 1. 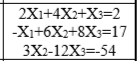 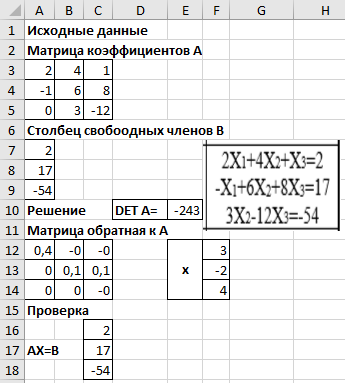 Листы переименовал. Сохранил файл PDF. ЛАБОРАТОРНАЯ РАБОТА НОМЕР 11: Построение поверхностей в трехмерном пространстве Цель работы: Изучение графических возможностей пакета Ms Excel. Приобретение навыков построения графика функции в трехмерном пространстве. Задание 5.1. Построить верхнюю часть эллипсоида: 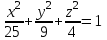 Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z. 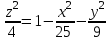 >>>>> >>>>> 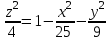 >>>> >>>> 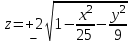 Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения: 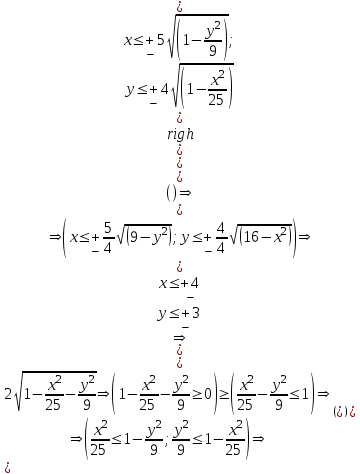 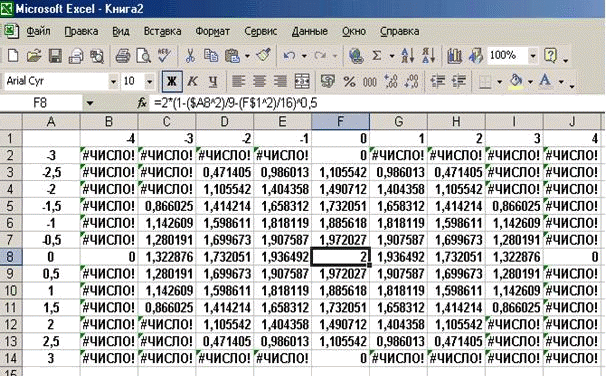 Перейдем к построению поверхности. 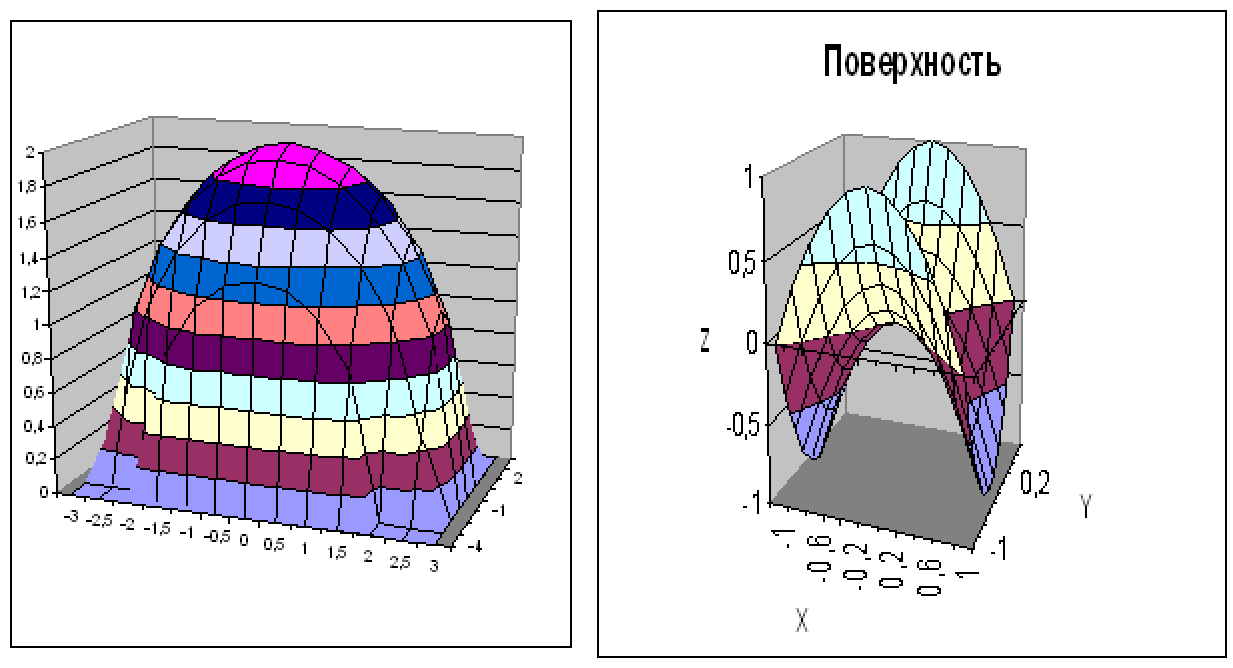 Задание 5.2: Построить однополостный (четные варианты) или двуполостный (нечетные варианты) гиперболоид, заданного уравнением: 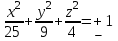 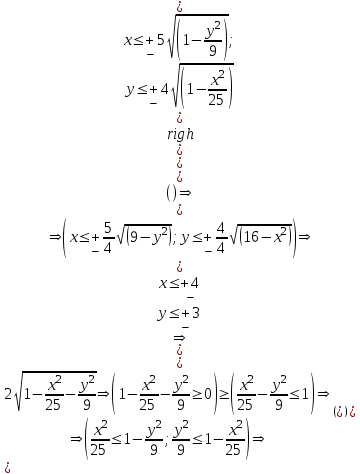 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
