Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
2)Напряженность и потенциал электрического поля. Связь между ними. Энергия взаимодействия системы зарядов.Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля. E = F / q пр. Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда. Напряженность поля точечного заряда. Используя закон Кулона найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда: 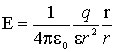 (1.2) (1.2)В этой формуле r – радиус-вектор, соединяющий заряды qи qпр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q> 0 и к заряду при q< 0. Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q1, q2, q3, , qn, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности: 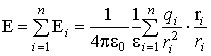 где ri – расстояние между зарядом qiи рассматриваемой точкой поля. Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq. Тело, которое находится в потенциальном поле сил ,обладает потенциальной энергией, за счет которой силы поля совершают работу. Как известно из классической механики, работа консервативных сил совершается за счет убыли потенциальной энергии. Значит работу сил электростатического поля можно считать как разность потенциальных энергий, которыми обладает точечный электрический заряд Q0 в начальной и конечной точках поля заряда Q: откуда мы видим, что потенциальная энергия заряда Q0 в поле заряда Q равна Она, как и в классической механике, определяется неоднозначно, а с точностью до произвольной постоянной С. Если считать, что при перенесении заряда в бесконечность (r→∞) потенциальная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0, который находится в поле заряда Q на расстоянии r от него, равна Для зарядов одинакового знака Q0Q>0 потенциальная энергия их взаимодействия (в данном случае - отталкивания) положительна, для разноименных зарядов Q0Q<0 и потенциальная энергия их взаимодействия (в данном случае - притяжения) отрицательна. Если поле создается системой n точечных электрических зарядов Q1, Q2, ..., Qn, то работа электростатических сил, которая совершается над зарядом Q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q0, который находится в этом поле, равна сумме потенциальных энергий Ui, каждого из зарядов: Из формул (2) и (3) следует, что отношение U/Q0 не зависит от Q0 и является поэтому энергетической характеристикой электростатического поля, которая называется потенциалом: Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формул (4) и (2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен Работа, которую совершают силы электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (1), (4), (5)), может быть выражена как |
