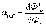Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля

• Название: Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
• Анкор: Fizika_Otvety.docx
• Дата: 07.02.2018
• Размер: 1.66 Mb.
• Имя файла: Fizika_Otvety.docx
• Тип: Закон; #15311
• страница: 29 из 29

44)Дисперсия света.

Дисперсией света называется зависимость преломления n вещества от частоты w ( или длины волны ). Эту зависимость можно охарактеризовать функцией :

n=f(w)

С увеличением частоты показатель преломления возрастает : dn/dw > 0. В этом случае дисперсия называется нормальной. Если вещество поглощает часть лучей, то в области поглощения дисперсия обнаруживает аномалию – показатель преломления при увеличении частоты уменьшается : dn/dw <0. Такой ход зависимости n от w называется аномальной дисперсией.

Дисперсия света может быть также объяснена на основе электромагнитной теории и электронной теории вещества. Для этого нужно рассмотреть процесс взаимодействия света с веществом. Итак, абсолютный показатель преломления среды , равен :

где  - диэлектрическая проницаемость среды, - магнитная проницаемость. В оптической области спектра для всех веществ  1, поэтому

(186.1)

Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.

Применим электронную теорию дисперсии света для однородного диэлектрика, предположив формально, что дисперсия света является следствием зависимости  от частоты световых волн. Диэлектрическая проницаемость вещества, по определению равна



где æ- диэлектрическая восприимчивость среды, ₀ - электрическая постоянная, Р - мгновенное значение поляризованности. Следовательно,



(186.2)

т. е. зависит от Р. В данном случае основное значение имеет электронная поляризация, т. е. вынужденные колебания электронов под действием электрической составляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока (v  10¹⁵ Гц).

В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные с ядром электроны - оптические электроны. Для простоты рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р = ех, где е - заряд электрона, х - смещение электрона под действием электрического поля световой волны. Если концентрация атомов в диэлектрике равна n₀ то мгновенное значение поляризованности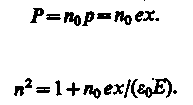

(186.3) (186.4)

Следовательно, задача сводится к определению смещения х электрона под действием внешнего поля Е. Поле световой волны будем считать функцией частоты со, т. е. изменяющимся по гармоническому закону: E = E₀cost.

Уравнение вынужденных колебаний электрона (см. § 147) для простейшего случая (без учета силы сопротивления, обусловливающей поглощение энергии падающей волны) запишется в виде

(186.5)

где F₀ = eE₀- амплитудное значение силы, действующей на электрон со стороны поля волны, - собственная частота колебаний электрона, m - масса электрона. Решив уравнение (186.5), найдем  = n² в зависимости от констант атома (е, m, ₀) и частоты внешнего поля, т. е. решим задачу дисперсии. Решение уравнения (186.5) можно записать в виде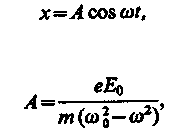

(186.6) (186.7)

в чем легко убедиться подстановкой (см. (147.8)). Подставляя (186.6) и (186.7) в (186.4), получим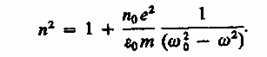

(186.8)

Если в веществе имеются различные заряды e_hсовершающие вынужденные колебания с различными собственными частотами еа_0|, то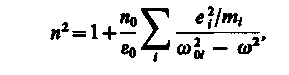

(186.9)

где m₁ - масса i-го заряда.

Из выражений (186.8) и (186.9) вытекает, что показатель преломления л зависит от частоты внешнего поля, т. е. полученные зависимости действительно подтверждают явление дисперсии света, хотя и при указанных выше допущениях, которые в дальнейшем надо устранить. Из выражений (186.8) и (186.9) следует, что в области от  = 0 до  = ₀n²больше единицы и возрастает с увеличением (нормальная дисперсия); при  = ₀n² = ± ; в области от  = ₀ до  = n² меньше единицы и возрастает от -  до 1 (нормальная дисперсия). Перейдя от n² к n, получим, что график зависимости n от имеет вид, изображенный на рис. 270.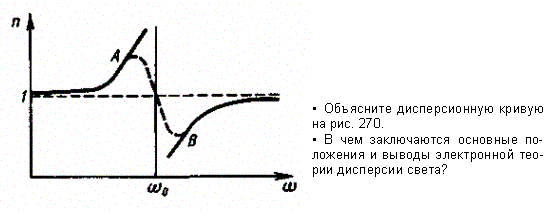



Рис. 270

 

Такое поведение n вблизи ₀ - результат допущения об отсутствии сил сопротивления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции л (со) вблизи too задается штриховой линией АВ. Область АВ - область аномальной дисперсии (n убывает при возрастании ), остальные участки зависимости n от  описывают нормальную дисперсию (n возрастает с возрастанием ).

45) Тепловое излучение

Тепловое излучение – процесс распространения электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. Возникновение потока лучей в результате превращения тепловой энергии в лучистую, называется излучением или лучеиспусканием, а обратный переход лучистой энергии в тепловую называют поглощением лучей.

Количественной характеристикой теплового излучения является спектральная плотность энергетической светимости (излучательности) тела – мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины:

,

где – энергия электромагнитного излучения, испускаемого за единицу времени с единицы площади поверхности тела (мощность излучения) в интервале частот  до +d.
В зависимости от температуры излучающего тела его лучеиспускание различно. При температуре ниже 500°С только незначительная часть всех лучей воспринимается глазом как “свет”, а наибольшая часть приходится на долю невидимого теплового излучения. Интенсивность теплового излучения характеризуется излучательной (лучеиспускательной) способностью тела, имеющего температуру Т: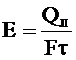

                                                               ,                                                 (2.1)

где Q_л – полное количество теплоты, Дж; F – поверхность излучающего тела, м²; τ – время, с.

Лучеиспускательная способность тела есть количество энергии, излучаемое в единицу времени единицей поверхности нагретого тела, имеющего температуру Т, в окружающую среду с температурой абсолютного нуля. Для абсолютно черного тела связь между излучательной способностью и абсолютной температурой выражается законом Стефана-Больцмана:

                                                            ,                                               (2.2)

где  К_о – константа излучения абсолютно черного тела, К_о=5,67·10^-8 Вт/(м²·К⁴); Т – абсолютная температура поверхности тела, К; E_о – излучательная способность черного тела, Вт/м².

 Пусть на элементарную площадку поверхности тела падает поток лучистой энергии , обусловленный электромагнитными волнами, частоты которых заключены в интервале dν. Часть этого потока будет поглощаться телом. Безразмерная величина

(1.2.2)

называется поглощательной способностью тела. Она также сильно зависит от температуры.

Закон Кирхгофа

 

Отношение спектральной плотности энергетической светимости(излучения) к спектральной поглощательной способности(поглощения) не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа):

 

. (7.1)

Из закона Кирхгофа вытекает, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при одинаковых значениях Т и ), так как и поэтому . Кроме того, из (7.1) видно, что если тело при данной температуре Т не поглощает электромагнитные волны в интервале частот от  до +d, то оно их в этом интервале частот при температуре Т и не излучает, так как и .

Абсолютно чёрное тело.

Пусть одно из тел в полости обладает свойством поглощать всю падающую на его поверхность лучистую энергию любого спектрального состава. Такое тело называют абсолютно черным. При заданной температуре собственное тепловое излучение абсолютно черного тела, находящегося в состоянии теплового равновесия с излучением, должно иметь тот же спектральный состав, что и окружающее это тело равновесное излучение. В противном случае равновесие между абсолютно черным телом и окружающем его излучением не могло бы установиться. Поэтому задача сводится к изучению спектрального состава излучения абсолютно черного тела. Решить эту задачу классическая физика оказалась не в состоянии.

Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно поглощает. Это одна из важнейших закономерностей теплового излучения. Отсюда следует, что при заданной температуре абсолютно черное тело испускает с поверхности единичной площади в единицу времени больше лучистой энергии, чем любое другое тело.

Рисунок 5.1.1. Модель абсолютно черного тела

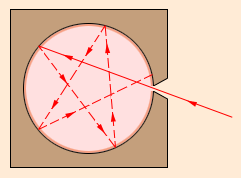
Абсолютно черных тел в природе не бывает. Хорошей моделью такого тела является небольшое отверстие в замкнутой полости (рис. 5.1.1). Свет, падающий через отверстие внутрь полости, после многочисленных отражений будет практически полностью поглощен стенками, и снаружи отверстие будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела

Формула Планка

Выдающийся немецкий физик Макс Планк ,изучая тепловое излучение, открыл его атомный характер. Он рассматривал модель черного тела, представлявшую собой совокупность электромагнитных осцилляторов, излучающих и поглощающих электромагнитную энергию каждый определенной частоты. Планк принял гипотезу, что каждый осциллятор излучает и поглощает энергию конечными порциями — квантами. В 1900 году Планк доложил Берлинскому физическому обществу о своей гипотезе и новой формуле излучения.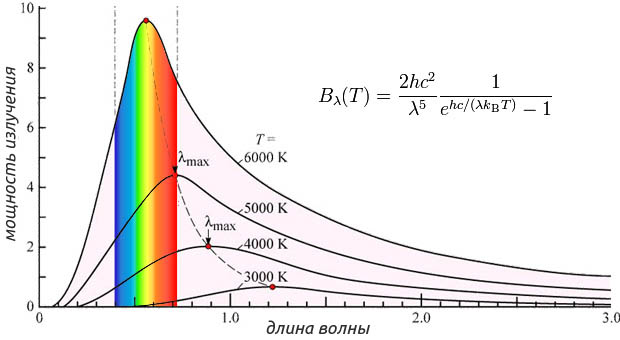



Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Площадь под кривой соответствует суммарной мощности излучения по закону Стефана-Больцмана. Открытие Планка заложило основу развития квантовой физики.

Закон Стефана — Больцмана

Австрийский физик и математик Йозеф Стефан (Joseph Stefan) в 1879 году путём измерения теплоотдачи платиновой проволоки при различных температурах установил пропорциональность излучаемой ею энергии четвертой степени абсолютной температуры. Теоретическое обоснование этого закона было дано в 1884 году учеником Стефана Людвигом Больцманом (Ludwig Boltzmann).

Энергетическая светимость (q) абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры (T).

q = σ ⋅ T⁴

Константа в этой формуле называется постоянной Стефана-Болъцмана, σ = 5.67⋅10^-8 (Вт/м²)/К⁴. Энергетическая светимость — это мощность излучения на всех длинах волн с единицы поверхности (Вт/м2). Из этого следует, что все окружающие нас объекты испускают тепловое излучение, так как всегда имеют температуру выше абсолютного нуля 0 К или минус 273ºС. При повышении абсолютной температуры в два раза, мощность излучения увеличится в 16 раз. Закон справедлив для излучения Абсолютно черного тела.

Закон Вина

Важные результаты в термодинамике излучения были получены немецким физиком Вильгельмом Вином (Wilhelm Wien). В 1893 году Вин на основе термодинамических соображений впервые вывел закон, определяющий положение максимума в распределении энергии в спектре излучения АЧТ. Закон показывает, как смещается максимум распределения энергии в спектре излучения абсолютно чёрного тела при изменении температуры.

Длина волны (λмакс), на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре (Т) абсолютно черного тела.

λ_макс = b / T

В приведенной формуле постянная b = 2,897⋅10^-3 м·К, чтобы получить результат вычисления λ_макс в мкм следует взять значение b = 2897 мкм·К. Например, при температуре 36°С максимум излучения приходится на 9,4 мкм. При температуре порядка 6000 К (темература поверхности Солнца) максимум излучения приходится на 0,47 мкм (соответствует желтовато-белому).

Законы Планка и Вина объясняют, почему вещество при нагреве начинает светиться в видимом спектре. Как видно из формул, при повышении температуры объекта, все больше излучения испускается с короткими длинами волн. Начиная с температуры около 500°С это излучение уже можно наблюдать невооруженным глазом.

*: