Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
38)Дифракция света.Дифракцией называется совокупность явления, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция , в частности , приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Между интерференцией и дифракцией не существует физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Перераспределение интенсивности , возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками , расположенным непрерывно, принято называть дифракцией волн. Принцип Гюйгенса Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис.3). Этот принцип в равной мере пригоден для описания распространения волн любой природы: механических, световых и т. д. Гюйгенс сформулировал его первоначально именно для световых волн. 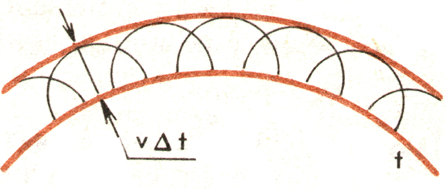 Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют. Зоны Френеля. Френель решил задачу нахождения амплитуды в т. Р, заменив интегрирование суммированием, т.е. перешёл от непрерывных сумм () к дискретным (Σ). 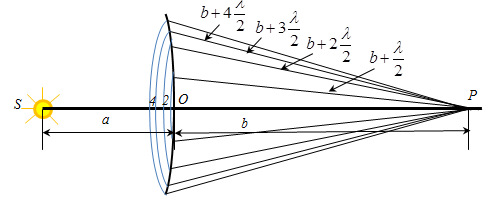 Точечный источник S создаёт сферическую волну. Требуется определить амплитуду колебаний волны в т. Р. Волновая поверхность в некоторой точке О будет представлять сферу. Френель предложил разбить ее на кольцевые зоны (секторы) так, что расстояния от краев каждой зоны до т. Р отличается на λ/2. Построенные таким образом сектора сферы называются зонами Френеля. Волны, приходящие в т. Р от аналогичных точек двух соседних зон имеют противоположные фазы, т.к. разность хода между этими волнами равна λ/2. При не слишком больших m (m – номер зоны), площади зон Френеля примерно равны S1= S2 =Sm. С ростом номера зоны m увеличивается расстояние bm, от зоны до т. Р и угол φ между нормаль. к элементам зоны и направлением на т. Р. Тогда по формуле (1) амплитуда Am колебания, возбуждаемогоm -й-зоной в т. Р, монотонно убывает А1 >A2 >A3 >Am >…>A∞. Т.к. волны от двух соседних зон приходят в т. Р в противофазе, они ослабляют друг друга и тогда результирующая амплитуда в т. Р равна Арез = А1 -A2 +A3 –A4+… Т.к. Am монотонно убывает, то можно считать и Арез можно записать в виде Если фронт волны полностью открыт, то число зон m → ∞ и Амплитуда, создаваемая в некоторой точке Р всей сферической волновой поверхностью, равна половине амплитуды первой зоны. Следовательно, распространение света от S к Р происходит так, будто световой поток распространяется внутри очень узкого канала вдоль линии SР. т. е. прямолинейно. Если на пути световых волн поставить экран с отверстием, в котором укладывается четное число зон Френеля, то в т. Р будет минимум – ослабление света. Если в отверстии укладывается нечетное число зон Френеля, то в т. Р будет максимум - усиление света Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как теперь зоны Френеля нужно строить не на плоской, а на сферической поверхности .Расчет приводит к следующему выражению для радиусов ρm зон Френеля на сферическом фронте волны:
|
