Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
37)Интерференция в тонких плёнках.При падении световой волны на тонкую прозрачную плёнку или пластинку происходит отражение от обеих поверхностей пленки. В результате возникают две световые волны, которые при известных условиях могут инерферировать. Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна, которую можно рассмотреть как параллельный пучок лучей. На рисунки изображен один из лучей этого пучка. Пластинка отбрасывает вверх два параллельных пучка света, один из которых образуется за счёт отражения от верхней поверхности пластинки, другой – вследствие отражения от нижней поверхности. При входе в пластинку и при выходе из нее второй пучок претерпевает преломление. Коэффициент отражения на границах воздух - пластинка и пластинка – воздух одинаков и для стекла, равен примерно 5%. Поэтому интенсивность обоих отраженных пучков практически одинакова. Кроме пучков 1 и 2 пластинка отбросит вверх пучки, возникающие в результате трех-, пяти-, и т.д кратного отражения от поверхности пластинки. Однако ввиду малой интенсивности эти пучки можно не принимать во внимание. Если оптическая разность хода лучей 1 и 2 будет существенно меньше длины когерентности исходной волны, то волны, представленные этими лучами, будут когерентными и смогут интерферировать. На дальнейшем пути лучей от точек A и B разность фаз волн 1 и 2 не изменяется. Поэтому оптическая разность хода лучей 1 и 2 : 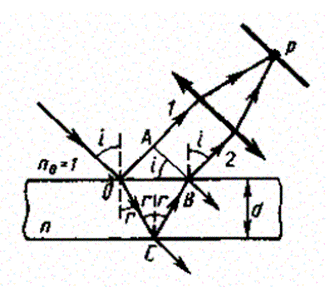 =ns2 – s1 S1 – длинна отрезка OA, s2 – суммарная длина отрезков OC и CB, n – показатель преломления пластинки. Полосы равного наклона Пусть тонкая плоскопараллельная пластинка освещается рассеянным квазимонохроматическим светом. Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом , после отражения от поверхности пластинки, соберутся линзой в точке P и создадут в этой точке освещенность, определяемую значением оптической разности хода. Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом , соберутся линзой в других точках, отстоящих от центра экрана O на такое же расстояние, как и точка P. Освещенность во всех этих точках будет одинакова. Таким образом, лучи, падающие на пластинку под одинаковым углом, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром в O. Аналогично лучи, падающие под другим углом, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности другого радиуса. В результате на экране возникнет система чередующихся светлых и темных круглых полос с общим центром в точке O. Каждые расположены под одинаковым углом. Эти полосы называются полосами равного наклона. 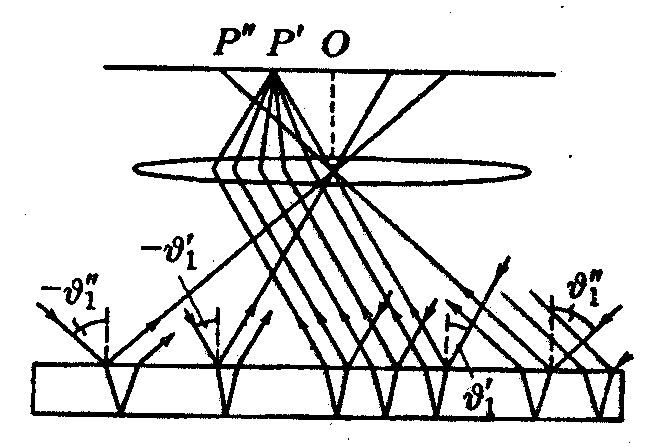 Полосы равной толщины 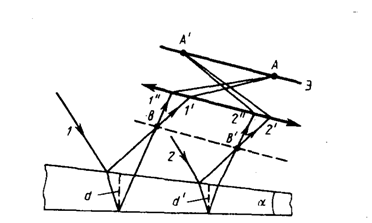 Рассмотрим пластинку в виде клина с углом при вершине ФИ. Пусть на нее падает параллельный пучок лучей. Теперь лучи, отразившиеся от разных поверхностей пластинки, не будут параллельными. Они пересекаются в точках B, B” и т.д. Можно показать, что эти и другие аналогичные им точки лежат в одной плоскости, проходящей через вершину клина O. При малом угле клина ФИ разность хода лучей можно с достаточной точностью вычислять по формуле : =ns2 – s1, беря в качестве b толщину пластинки в месте падения на нее лучей. Поскольку разность хода лучей, отразившихся от различных участков клина, теперь неодинакова, освещенность экрана будет неравномерной – на экране появятся светлые и тёмные полосы. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие этого их называют полосами равной толщины. Кольца Ньютона Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.15). Роль тонкой пленки, от поверхности которой отражаются волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов. 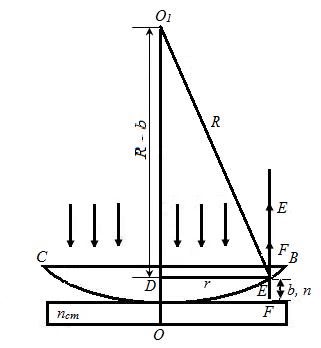 Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае и . Из рис. видно, что , где – радиус кривизны линзы, – радиус окружности, всем точкам которой соответствует одинаковый зазор . Величиной можно пренебречь, тогда . Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно добавить к разности хода :
В точках, для которых , возникнут максимумы интенсивности, а в точках, для которых 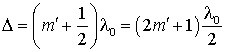 – минимумы интенсивности. – минимумы интенсивности. Оба условия можно объединить в одно:
четным будут соответствовать максимумы, а нечетным – минимумы интенсивности. Подставив (2.18) в (2.17), получим радиусы темных и светлых колец Ньютона:
Четным соответствуют радиусы светлых колец, нечетным – радиусы темных колец. Значению соответствует , то есть в месте касания пластинки и линзы наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки. |
