Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля

• Название: Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
• Анкор: Fizika_Otvety.docx
• Дата: 07.02.2018
• Размер: 1.66 Mb.
• Имя файла: Fizika_Otvety.docx
• Тип: Закон; #15311
• страница: 5 из 29

6)Вектор электрической индукции :

Имея дело с электростатическим полем в пустоте, мы вводили в рассмотрение линии напряженности. Линии напряженности в пустоте обладают тем свойством, что они тянутся непрерывно от одних зарядов до других или уходят в бесконечность. Не так обстоит дело в диэлектриках, если учитывать одни только свободные заряды. Например, на границах раздела диэлектриков возникнут связанные поверхностные заряды, и часть линий напряженности будет на них заканчиваться или с них начинаться. Таким образом, линии напряженности не пройдут непрерывно границу раздела диэлектриков. Поэтому в неоднородных диэлектриках перестает иметь смысл и теорема Остроградского — Гаусса в том виде, как она была дана раньше.

Необходимо ввести для характеристики поля внутри диэлектрика такой новый вектор D, линии которого пойдут через диэлектрик, а также через границы их раздела непрерывно. Этот вектор называется вектором электростатической индукции; он связан с вектором напряженности Е соотношением:

D = ε0ε E

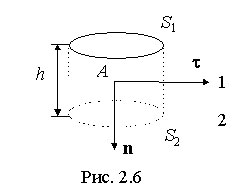
Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

   (1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие - заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

(1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности.

7)Уравнения Максвела для электростатического поля в веществе.

1. Первое уравнение Максвелла представляет собой закон Гаусса для электрических полей. Максвелл записал его в дифференциальной форме. В современной записи оно выглядит так :

·E = ρ/ε_o

где:

E – векторное электрическое поле (здесь и далее жирным шрифтом выделены векторные величины, а курсивом - скалярные);

· – значок оператора дивергенции (потока);

ρ – суммарный заряд;

ε_o – диэлектрическая постоянная вакуума.

Оно говорит том, что поток электрического поля Е через любую замкнутую поверхность зависит от суммарного электрического заряда внутри этой поверхности. Иначе говоря, если из замкнутого бассейна вытекает воды больше, чем в него втекает (то есть суммарный поток из бассейна получается больше нуля), то ясно, что внутри бассейна прячется труба – источник этой самой воды (иначе бы она быстро кончилась).

С электрическим полем то же самое: если есть электрический заряд (труба-источник воды в бассейне), то поле от него будет вытекать наружу во все стороны (вода будет выливаться через края).

Рассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков с проницаемостями и при отсутствии на границе зарядов Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6). Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность . Выделяя потоки через основания и боковую поверхность цилиндра , где - значение касательной составляющей усредненное по боковой поверхности . Переходя к пределу при (при этом также стремится к нулю), получаем , или окончательно для нормальных составляющих вектора электрической индукции . Для нормальных составляющих вектора напряженности поля получим . Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора терпит разрыв, а нормальная составляющая вектора непрерывна.