Ответы-физика-лет. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды

• Название: Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
• Дата: 09.12.2018
• Размер: 0.88 Mb.
• Имя файла: Ответы-физика-лет.doc
• Тип: Закон; #59379
• страница: 3 из 3

15.1. Магнитные моменты атомов.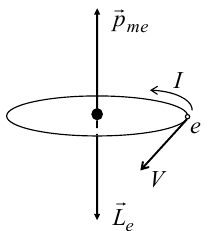

В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома (молекулы) равен векторной сумме магнитных моментов электронов, входящих в его состав (как показывают эксперименты, магнитные моменты ядер атомов ничтожно малы)




15.2. Типы магнетиков.

Вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками. В отсутствии внешнего магнитного поля диамагнетики немагнитны, т.к. у них суммарный магнитный момент атома (молекулы) равен нулю. Диамагнетизм свойственен всем веществам. Диамагнетиками являются висмут, Zn, Au, Ag, H2O, инертные газы, H2, N2 и многие другие элементы и соединения.

Наряду с диамагнитными веществами существуют и парамагнитные − вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.

У парамагнитных веществ магнитные моменты электронов, входящих в состав атомов (молекул), даже в отсутствии внешнего магнитного полы нескомпенсированы. Вследствие этого атомы (молекулы) парамагнетика обладают собственным магнитным моментом. Однако, из-за теплового движения эти магнитные моменты ориентированы беспорядочно, поэтому в отсутствии внешнего магнитного поля парамагнетики, так же как и диамаг-

нетики, немагнитны.

При внесении парамагнитного вещества во внешнее магнитное поле магнитные моменты электронов прецессируют относительно направления вектора B (диамагнитное явление), и, в то же время, устанавливается преимущественная ориентация магнитных моментов атомов вдоль поля. Эффект от этого значительно больше, чем от проявления диамагнитных свойств. В итоге индукция магнитного поля в парамагнетике увеличивается. К

парамагнетикам относятся щелочные металлы, редкоземельныеэлементы, некоторые газы (Na, K, Al, Pt, O2, NO и др.).

Наряду с рассмотренными выше слабомагнитными веществами, существуют еще сильномагнитные вещества − ферромагнетики − вещества, обладающие самопроизвольной (спонтанной) намагниченностью, которая сильно зависит от внешних воздействий − магнитного поля, температуры, деформаций. К ферромагнетикам относятся железо, никель, кобальт, гадолиний, их сплавы и некоторые соединения.

15.3. Микро- и макротоки.

При изучении магнитного поля в веществе различают два вида токов: макротоки I и микротоки I′. Макротоки − это электрические токи проводимости. Микротоки (молекулярные токи) − токи, обусловленные движением электронов в атомах, ионах, молекулах.

В магнетике на магнитное поле макротоков (внешнее магнитное поле) накладывается дополнительное поле микротоков (внутреннее).

15.4. Вектор намагничивания.

15.5. Описание магнитного поля в веществе.

15.6. Магнитная восприимчивость и магнитная проницаемость.

16.1. Напряженность магнитного поля.

Вектор

называется напряженностью магнитного поля.

16.2. Закон полного тока для магнитного поля в веществе.


16.3. Условия для векторов напряженности и индукции магнитного поля на

границе раздела двух магнетиков.

17.1. Магнитный момент атома.

Магнитный момент атома (молекулы) равен векторной сумме магнитных моментов электронов, входящих в его состав (как показывают эксперименты, магнитные моменты ядер атомов ничтожно малы).

Согласно представлениям классической физики электрон в атоме движется по круговым орбитам. При этом каждый электрон эквивалентен круговому току. Сила орбитального тока
где ν − частота вращения электрона на орбите, е − его заряд. Орбитальному току соответствует магнитный момент pmе − орбитальный магнитный момент электрона.



17.2. Элементарная теория диамагнетизма и парамагнетизма.

Будем считать, что электрон в атоме движется по круговой орбите и его орбитальный магнитный момент p me составляет угол α с вектором индукции магнитного поля B . Можно показать, что под влиянием внешнего магнитного поля вектор p me будет вращаться вокруг направления B , сохраняя постоянным угол α. Такое движение называется прецессией. Наличие прецессии орбиты эквивалентно появлению дополнительного орбитального тока, направление которого таково, что его магнитный момент направлен противоположно внешнему магнитному полю. Наведенные составляющие магнитных моментов электронов атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле.

Этот эффект носит название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками. В отсутствии внешнего магнитного поля диамагнетики немагнитны, т.к. У них суммарный магнитный момент атома (молекулы) равен нулю. Диамагнетизм свойственен всем веществам. Диамагнетиками являются висмут, Zn, Au, Ag, H2O, инертные газы, H2, N2 и многие другие элементы и соединения.

Наряду с диамагнитными веществами существуют и парамагнитные − вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.

У парамагнитных веществ магнитные моменты электронов, входящих в состав атомов (молекул), даже в отсутствии внешнего магнитного полы нескомпенсированы. Вследствие этого атомы (молекулы) парамагнетика обладают собственным магнитным моментом. Однако, из-за теплового движения эти магнитные моменты ориентированы беспорядочно, поэтому в отсутствии внешнего магнитного поля парамагнетики, так же как и диамагнетики, немагнитны.

При внесении парамагнитного вещества во внешнее магнитное поле магнитные моменты электронов прецессируют относительно направления вектора B (диамагнитное явление), и, в то же время, устанавливается преимущественная ориентация магнитных моментов атомов вдоль поля. Эффект от этого значительно больше, чем от проявления диамагнитных свойств. В итоге индукция магнитного поля в парамагнетике увеличивается. К

парамагнетикам относятся щелочные металлы, редкоземельные элементы, некоторые газы (Na, K, Al, Pt, O2, NO и др.).

18.1. Ферромагнетизм.

Наряду с рассмотренными выше слабомагнитными веществами, существуют еще сильномагнитные вещества − ферромагнетики − вещества, обладающие самопроизвольной (спонтанной) намагниченностью, которая сильно зависит от внешних воздействий − магнитного поля, температуры, деформаций. К ферромагнетикам относятся железо, никель, кобальт, гадолиний, их сплавы и некоторые соединения.

18.2. Опыты Столетова. Кривая намагничивания. Магнитный гистерезис.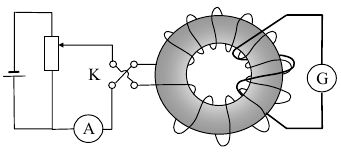

Тороид, первичная обмотка которого состояла из N1 витков, имел сердечник из исследуемого материала (например, железа). Вторичная обмотка из N2 витков была замкнута на баллистический гальванометр G, измеряющих заряд, в прошедшем через него импульсе тока. Первичная обмотка включалась в цепь источника э.д.с., силу тока I в ней I можно было изменять с помощью потенциометра. Направление тока можно изменять

коммутатором К.

При изменении направления тока в первичной обмотке с помощью коммутатора на противоположное, в цепи вторичной обмотки возникал импульс индукционного тока, и через баллистический гальванометр проходил электрический заряд q. Как будет показано далее, этот заряд равен отношению взятого с обратным знаком изменения полного магнитного потока сквозь вторичную обмотку к электрическому сопротивлению R цепи гальванометра



где Ф0m − магнитный поток сквозь один виток. Если сердечник тонкий, а площадь его поперечного сечения S, то индукция магнитного поля в сердечнике


Напряженность магнитного поля в сердечнике можно вычислить, используя закон полного тока


где lср − длина средней линии сердечника. Зная В и Н , можно найти намагниченность ферромагнетика


Опыты показали, что для ферромагнетиков наблюдается явление гистерезиса (запаздывание). Суть явления состоит в том, что намагниченность вещества неоднозначно зависит от напряженности магнитного поля. При Н=0 намагниченность J>0, т.е. в ферромагнетике наблюдается остаточная намагниченность Jос, что объясняет существование

постоянных магнитов.

18.3. Точка Кюри.

Остаточная намагниченность ферромагнетика может быть нарушена при его сотрясении. Аналогично действует нагревание ферромагнетика. С повышением температуры остаточная намагниченность уменьшается, и при достаточно высокой температуре, называемой точкой Кюри, она исчезает полностью. При тем пературах выше точки Кюри ферромагнетик ведет себя во внешнем магнитном поле как парамагнитное вещество.

18.4. Домены.

Спонтанная поляризация является источником очень больших электрических полей. Но с большим электрическим полем связана большая энергия. Известно, что любая система всегда стремится перейти в состояние с наименьшей энергией. Поэтому сегнетоэлектрик переходит в такое состояние, при котором с одной стороны существует спонтанная поляризация, а с другой − энергия его минимальна.

Это может осуществиться в результате разделения объема сегнетоэлектрика на малые области в каждой из которых имеется спонтанная поляризация в некотором направлении. Такие области называются диэлектрическими доменами.

Из−за хаотичной ориентации спонтанной поляризации отдельных доменов в отсутствии внешнего электрического поля дипольный момент кристалла диэлектрика равен нулю. При наложении электрического поля происходит частичная переориентация доменов, а также рост одних доменов за счет других.

19.1. Явление электромагнитной индукции.

19.2. Правило Ленца.

19.3. Закон электромагнитной индукции Фарадея-Максвелла и его вывод.

20.1. Явление самоиндукции.

20.2. Индуктивность.

20.3. Взаимная индуктивность.

20.4. Энергия магнитного поля, плотность энергии магнитного поля.

21.1. Закон электромагнитной индукции и.

Закон электромагнитной индукции - ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.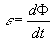


21.2. Первое уравнение Максвелла

Первое уравнение Максвелла является обобщением закона полного тока и в дифференциальной форме записывается как


22.1. Ток смещения.

При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высоких частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения "прохождения" переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.

Ток смещения существует и в проводниках по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока


22.2. Закон полного тока.

Для магнитного поля в вакууме



Для произвольной среды



22.3. Второе уравнение Максвелла.

Второе уравнение Максвелла является обобщением закона индукции Фарадея и в дифференциальной форме записывается так


23.1. Система уравнений Максвелла для электромагнитного поля в интегральной форме.

24.1. Система уравнений Максвелла для электромагнитного поля в дифференциальной форме.

25.1. Гармонические колебания (механические и электромагнитные, примеры) и их характеристики.

Колебаниями называют процессы, точно или приблизительно повторяющиеся во времени.

Если изменения во времени колеблющейся величины происходят по закону синуса или косинуса, то такие колебания называются гармоническими. Они описываются уравнением типа:



Величина x называется смещением. Смещение – это координата колеблющейся точки, которую отсчитывают от положения равновесия. Стоящая в скобках величина называется фазой колебаний.

Фаза колебаний – это аргумент, функцией которого является состояние колебательной системы в каждый момент времени. Фаза измеряется в угловых единицах – радианах (долях π). Значение фазы в момент t = 0 называется начальной фазой колебаний. Выбор начального момента совершенно произволен. Можно выбрать этот момент так, что начальная фаза будет равна нулю.

Поскольку функция косинус изменяется в пределах от -1 до +1, то смещение х может принимать значения − A ≤ x ≤ A . Максимальная величина смещения называется амплитудой.

25.2. Дифференциальное уравнение свободных незатухающих гармонических колебаний и его решение.



Решение этого уравнения имеет вид



25.3. Энергия гармонических колебаний.

Полная энергия механического движения является суммой кинетической и потенциальной энергий. Кинетическая энергия осциллятора - это энергия движущейся массы


Потенциальная энергия в точке x будет равна работе силы, совершаемой при перемещении груза из положения равновесия в данную точку, взятую с обратным знаком.


Выражение для полной энергии


где



25.4. Электрический колебательный контур.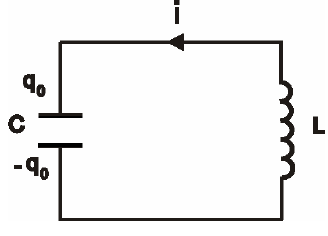








26.1. Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных, примеры) и его решение.



решение в случае малых затуханий



26.2. Логарифмический декремент и коэффициент затухания.

Количественной мерой затухания колебаний является величина, равная логарифму отношения амплитуд двух последовательных колебаний, отстоящих друг от друга на период



Отсюда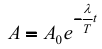



Величина, характеризующая действие силы трения, называется коэффициентом затухания и имеет размерность частоты колебаний.



где r - коэффициент трения, зависящий от свойств среды.

26.3. Добротность колебательного контура.

Добротность пропорциональна относительному изменению энергии затухающих колебаний за время одного периода колебаний



Добротность контура можно определить так


26.4. Апериодический процесс.

Период затухающих колебаний равен


При очень больших значениях коэффициента затухания ( β > ω0 ) под корнем стоит отрицательная величина. В этом случае частота колебаний становится мнимой, и, несмотря

на наличие сил, возвращающих систему в положение равновесия, колебания не возникают. Система возвращается в положение равновесия, асимптотически к нему приближаясь. Такое движение называется апериодическим.

27.1. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний.




F0 - амплитудное значение вынуждающей силы, ωв — частота внешней силы.

Избегая сложных математических выкладок, которые можно почерпнуть в литературе, запишем частное решение (его вещественную часть) уравнения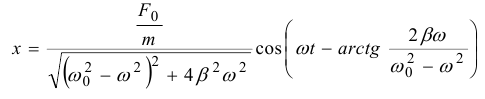




Выражение, стоящее перед функцией косинуса, представляет собой амплитуду вынужденных колебаний.

27.2. Резонанс.

Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынужденных колебаний приближается к собственной частоте колебательной системы, называется резонансом.

27.3. Резонансные кривые колебательного контура.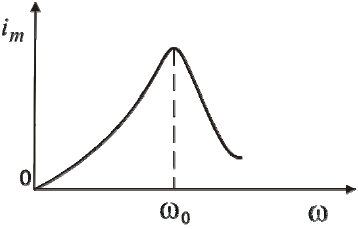