Ответы-физика-лет. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды

• Название: Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
• Дата: 09.12.2018
• Размер: 0.88 Mb.
• Имя файла: Ответы-физика-лет.doc
• Тип: Закон; #59379
• страница: 2 из 3

8.1. Законов Ома и Джоуля-Ленца в дифференциальной форме (вывод).

Закон Ома в дифференциальной форме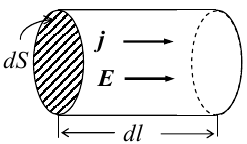

В изотропном проводнике направление векторов j и E совпадают. Выделим в проводнике трубкутока (поверхность, образованную линиями тока) в проводнике. Пусть площадь сечения ее dS а длина dl.

Ток через площадку dS будет




С другой стороны


или в векторном виде получаем соотношение, называемое законом Ома в дифференциальной форме



Дифференциальная форма закона Джоуля−Ленца

Применим закон Джоуля−Ленца к малому цилиндру длиной dl и площадью сечения dS, тогда получим


Введем удельную мощность тока, равную количеству тепла, выделившемуся в единице объема в единицу времени


Отсюда, используя закон Ома , получаем закон Джоуля−Ленца в дифференциальной форме



Можно также записать этот закон несколько в ином виде



9.1. Магнитное поле. Вектор магнитной индукции.

По аналогии с полевой трактовкой кулоновского взаимодействия, возникновение силы Ампера можно представить следующим образом: ток I1 рождает в окружающем пространстве магнитное поле; это магнитное поле действует на постоянные магниты или движущиеся заряды (ток I2).

Существование магнитного поля убедительно доказал в серии своих опытов по ориентирующему действию поля тока на магнитные стрелки Эрстед (1820 г.). Из опытов Эрстеда следует, что магнитное поле имеет направленный характер и, следовательно, должно характеризоваться векторной величиной. Эту величину называют магнитной индукцией и обозначают символом B.

Опыт показывает, что для магнитного поля, так же как и для электрического, справедлив принцип суперпозиции.

Вектор магнитной индукции B в данной точке поля совпадает по направлению с силой, которая действует на северный полюс бесконечно малой магнитной стрелки, помещенной в эту точку.

9.2. Закон Био-Савара- Лапласа и его применение к расчету полей прямого и кругового токов.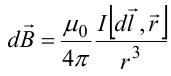



Направление вектора dB определяется правилом правого винта, которое заключается в

следующем: буравчик с правым винтом (штопор) нужно вращать от вектора dl к вектору r по

кратчайшему пути, тогда на правление движения острия бу равчика rпокажет ориентацию вектора dB .

Магнитное поле прямого тока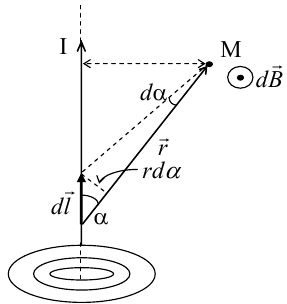

Рассчитаем, используя закон Био-Савара-Лапласа, магнит ное поле, создаваемое бесконечным прямым проводником с то ком, в точке М, отстоящей на расстоянии а от проводника.

Выделим элемент проводника dl. Пусть элемент dl виден из точки М под малым углом dα. Положение точки М относительно элемента dl определяется вектором r. Из

рис. видно, что выполняются следующие соотношения



Используя закон Био-Савара-Лапласа, запишем индукцию магнитного поля, создаваемого элементом тока dl в точке М


Для того, чтобы найти индукцию магнитного поля, создаваемого всем проводом, нужно, используя принцип суперпозиции, найти сумму векторов dBi от всех элементов dli.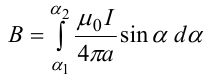


В случае бесконечного прямого тока α1=0 и α2=π, тогда


В общем случае индукция магнитного поля, создаваемого прямым проводником с ток конечной длины равна



odmin

Магнитное поле на оси кругового витка с током.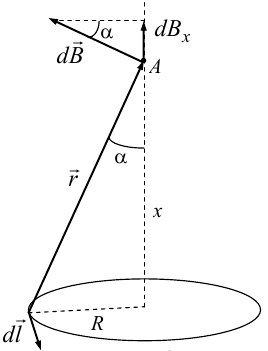

Возьмем на оси кругового витка точку А, отстоящую от плоскости витка на расстоянии х. Выберем ось х вдоль оси витка. Выделим на витке с током элемент тока dl. Оче видно, что при суммировании векторов dB от всех элементов витка горизонтальные составляющие векторов dB взаимно компенсируются, а вертикальные составляющие (dBx) складываются скалярно. Тогда индукция магнитного поля в точке А будет


здесь S − длина витка, R − его радиус.

Согласно закону Био-Савара-Лапласа



(угол между векторами r и dl равен π/2).
Окончательно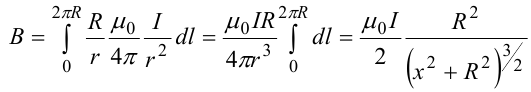



10.1. Закон полного тока (теорема о циркуляции вектора магнитной индукции).

В случае нескольких токов вrсилу принципа суперпозиции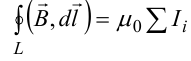


применение к расчету полей соленоида

10.2. Применение к расчету поля соленоида.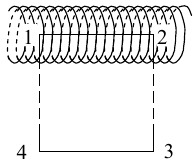

Рассмотрим бесконечно длинный соленоид по которому течет ток I и который имеет n витков на единицу длины. Выберем прямоугольный контур интегрирования 1-2-3-4. Сторона 1-2 совпадает с осью соленоида, а 3-4 удалена на очень большое расстояние от оси. В силу симметрии вектор B внутри соленоида дол жен быть параллелен его оси, т.е. Внутри соленоида магнитное поле должно быть однородно.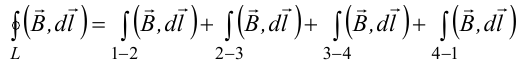



Последний интеграл в правой части равен нулю, т.к. На большом расстоянии от соленоида В=0. Второй и третий интегралы в правой части также равны нулю, т.к. для каждого элемента dl выполняется условие B ⊥ dl , а на участке 1-2, очевидно, B параллелен dl r. Тогда




, где l − длина участка 1-2.
С другой стороны, полученное выражение должно быть пропорционально сумме токов, охватываемых контуром 1-2-3-4. Рассматриваемый контур охватывает nl витков, в

каждом из которых течет ток I, тогда







Откуда

10.3. Поле тороида.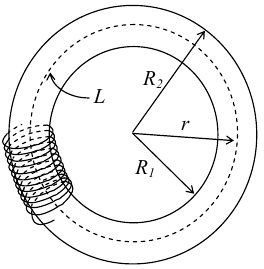

Пусть мы имеем тороид (”бублик”) с плотно намотанными на него N витками тонкого провода с током I. Пусть R1 и R2 − внешний и внутренний радиусы то роида. Найдем индукцию магнитного поля на средней линии тороида, т.е. на окружности радиуса r=(R1+R2)/2.

В качестве контура интегрирования L выберем саму среднюю линию. В силу симметрии вектор индукции магнитного поля B в каждой точке контура L должен быть направлен по касательной к этому контуру и быть постоянным по модулю. Выбранный нами контур охватывает все N витков.


Откуда


11.1. Закон Ампера.

Обобщая результаты опытов, Ампер сформулировал свой закон


где dF − сила, действующая на элемент dl проводника с током I, находящийся в магнитном поле с индукцией B. Направление вектора dF может быть найдено по общим правилам векторного произведения.

11.2. Взаимодействие параллельных проводников с током.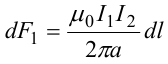


Сила взаимодействия двух параллельных проводников с током, приходящаяся на единицу длины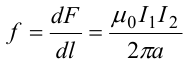


11.3. Силы, действующие на контур с током в магнитном поле.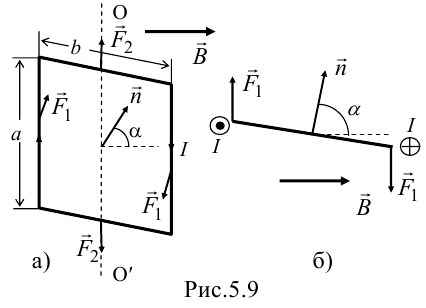

Возьмем прямоугольный контур, по которому течет ток I, находящийся в однородном магнитном поле с индукцией В. Пусть контур может вращаться относительно неподвижной оси ОО′. Длина сторон контура a и b.

Силы F1, действующие на вертикальные участки, равны


Плечо каждой из этих сил

Очевидно, что силы F2, действующие на горизонтальные участки контура, ориентированы вдоль оси ОО′ и они пытаются деформировать контур. Если контур достаточно жесткий, то эти силы в дальнейшем можно не учитывать.

12.1. Магнитный поток.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется физическая величина, равная



где Bn = B cos α − проекция вектора B на направление нормали к площадке dS (вектора n ), α − угол между векторами n и B, dS = dSn − вектор, модуль которого равен dS, а направление совпадает с направлением нормали к площадке. Обычно поток вектора B связывают с определенным контуром с током. В этом случае направление вектора n связано с направлением тока в контуре правилом правого винта.

Магнитный поток через произвольную поверхность S равен


12.2. Работа перемещения проводника и контура с током в магнитном поле (вывод).

Проводник с током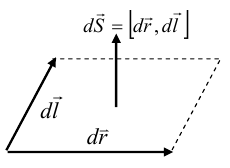

На проводник с током в магнитном поле действует сила Ампера. Элементарная работа δА, совершаемая силой Ампера dF при малом перемещении dr в постоянном магнитном поле малого элемента dl проводника сrтоком I, равна





При малом перемещении в магнитном поле проводника конечной длины l с током I силы Ампера совершают работу



где dФm − магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его перемещении на dr.

Если проводник, сила тока в котором поддерживается постоянной, совершает конечное перемещение в магнитном поле из положения 1 в положение 2, то работа сил Ампера на этом перемещения равна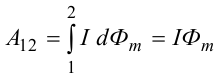



где Фm − магнитный поток сквозь поверхность, прочерчиваемую всем проводником при рассматриваемом перемещении.

Контур с током

Найдем работу сил Ампера по перемещению произвольного контура L с током I в магнитном поле.

Выберем элемент dl контура. При его перемещении на dr силы Ампера совершают работу



где d Фm эл − магнитный поток сквозь поверхность, которую проерчивает элемент dl при его перемещении на dr . Работа по перемещению всего контура будет равна

здесь d Фm − изменение магнитного потока через контур L.

При конечном перемещении контура из положения 1 в положение 2 работа будет равна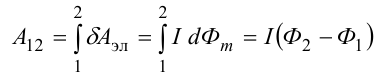


т.е. работа по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.

13.1. Действие магнитного поля на движущийся заряд. Сила Лоренца.

Естественно предположить, что на каждую частицу действует сила



В общем случае, если на движущуюся частицу помимо магнитного поля с индукцией B действует и электрическое поле с напряженностью E , то результирующая сила (сила Лоренца) равна сумме двух составляющихr− электрической и магнитной



13.2. Движение заряженных частиц в магнитном поле.

Пусть частица с зарядом q и массой m влетает в область, где существует постоянное магнитное поле, под углом α к линиям индукции. Представим скорость v частицы как сумму двух составляющих, − направленную вдоль поля v||=v cos α, и перпендикулярно полю v⊥=v sin α. Тогда силу Лоренца, действующую на частицу, можно представить в виде



т.е. составляющая скорости, параллельная полю, не вызывает появление магнитной силы.

Направление силы Лоренца перпендикулярно вектору скорости (траектории частицы), следовательно, сила Лоренца может изменять скорость только по направлению, а не по величине.

Следовательно, движение частицы можно представить в виде су перпозиции:

1) равномерного прямолинейного движения частицы вдоль поля со скоростью v||=v cos α;

2) равномерного движения со скоростью v⊥=v sin α по окружности в плоскости, перпендикулярной полю. Радиус окружности может быть найден из соотношений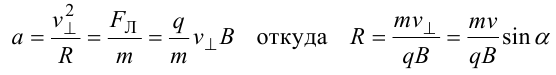


В результате сложения обоих движений возникает движение по спирали, ось которой направлена параллельно магнитному полю. Время одного полного оборота (период)


14.1. Эффект Холла.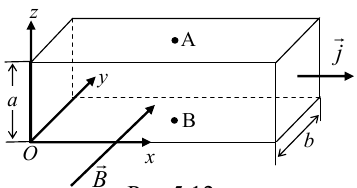

Эффект Холла (1879 г.) − это возникновение в металле или полупроводнике с током, помещенном в магнитное поле, разности потенциалов в направлении, перпендикулярном движению носителей тока.

Пусть ток с плотностью j в образце в виде прямоугольной пластины обусловлен упорядоченным движением частиц с зарядом q.

Поместим пластину в магнитное поле с индукцией B , перпендикулярное плотности тока j.

На частицу, движущуюся в магнитном поле, действует сила Лоренца . При указанных направлениях тока и магнитного поля сила Лоренца направлена вверх (вдоль положительного направления оси OZ). Под действием силы FЛ частицы будут отклоняться к верхней грани пластины, так что на ней будет накапливаться избыток зарядов того же знака, что и q, а на нижней грани − избыток зарядов противоположного знака. В результате этого в пластине возникнет поперечное электрическое поле, направленное сверху вниз, если q>0, и снизу вверх если q<0. Пусть Е − напряженность образовавшегося электрического поля. Сила qE , действующая на заряд q со стороны поперечного электрического поля, направлена в сторону, противоположную магнитной составляющей FЛ . В случае установившегося состоя-

ния сила Лоренца равна нулю



Разность потенциалов между точками А и В на гранях пластины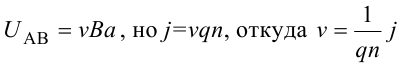


Тогда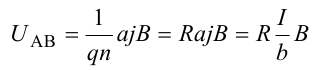


где R=1/(qn) − постоянная Холла.

14.2. Циклотрон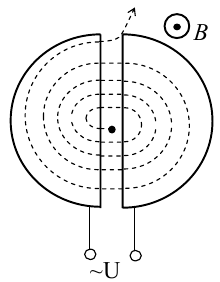

Циклотрон − ускоритель тяжелых частиц (протонов, ионов). В основе конструкции циклотрона − два полых электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное (ускоряющее) электрическое поле, и они находятся в вакуумной камере в сильном однородном магнитном поле, перпендикулярном плоскости дуантов.

Заряженные частицы вводятся в центр зазора между дуантами. В зазоре частица ускоряется электрическим и отклоняется магнитным полями. Войдя в дуант, частица описывает полуокружность, радиус которой пропорционален скорости частиц. Очевидно, условием ускорения частицы при каждом проходе зазора является равенство частот ω∼ ускоряющего электрического поля и частоты вращения частицы ωс.


Если амплитуда напряжения между дуантами U0, а число проходов частицы ускоряющей разности потенциалов n, то максимальная энергия, приобретенная частицей, будет



Максимально возможный радиус вращения частицы в магнитном поле (радиус дуантов)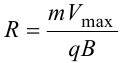


где Vmax − максимальная скорость частицы в циклотроне. Отсюда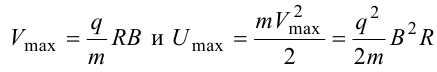


При достижении энергии частиц до максимального значения на последнем витке пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.

Циклотроны позволяют ускорять протоны до энергии ∼20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается.