Шпаргалка. билеты по физике. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
 Скачать 1.89 Mb.
|
|
14.2. Циклотрон 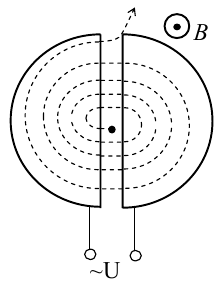 Циклотрон − ускоритель тяжелых частиц (протонов, ионов). В основе конструкции циклотрона − два полых электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное (ускоряющее) электрическое поле, и они находятся в вакуумной камере в сильном однородном магнитном поле, перпендикулярном плоскости дуантов.Заряженные частицы вводятся в центр зазора между дуантами. В зазоре частица ускоряется электрическим и отклоняется магнитным полями. Войдя в дуант, частица описывает полуокружность, радиус которой пропорционален скорости частиц. Очевидно, условием ускорения частицы при каждом проходе зазора является равенство частот ω∼ ускоряющего электрического поля и частоты вращения частицы ωс.  Если амплитуда напряжения между дуантами U0, а число проходов частицы ускоряющей разности потенциалов n, то максимальная энергия, приобретенная частицей, будет  Максимально возможный радиус вращения частицы в магнитном поле (радиус дуантов) 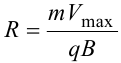 где Vmax − максимальная скорость частицы в циклотроне. Отсюда 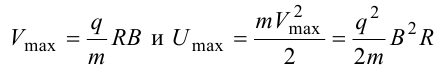 При достижении энергии частиц до максимального значения на последнем витке пучок частиц посредством отклоняющего электрического поля выводится из циклотрона. Циклотроны позволяют ускорять протоны до энергии ∼20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается. 15.1. Магнитное поле в веществе. Микро- и макротоки. При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками Характеризует магнитное поле в веществе вектор  15.2. Магнитные моменты атомов. 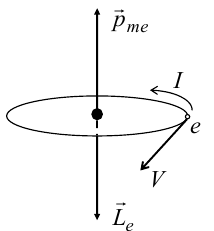 В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома (молекулы) равен векторной сумме магнитных моментов электронов, входящих в его состав (как показывают эксперименты, магнитные моменты ядер атомов ничтожно малы)  15.3. Вектор намагниченности. Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность , равная отношению магнитного момента малого объема вещества к величине этого объема: 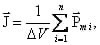 где  – магнитный момент i-го атома из числа n атомов, в объеме ΔV.15.4. Напряженность магнитного поля  15.5. Магнитная восприимчивость и магнитная проницаемость Намагниченность изотропной среды с напряженностью связаны соотношением:  где  – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением 16.1. Закон полного тока для магнитного поля в веществе.  16.2. Условия для векторов напряженности и индукции магнитного поля на границе раздела двух магнетиков. Рассмотрим границу двух однородных изотропных магнетиков, вдоль которой течет поверхностный ток проводимости с линейной плотностью . Пусть система находится в однородном магнитном поле. Используем теорему о полном магнитном потоке и теорему о циркуляции вектора напряженности  и  .Рассмотрим на границе замкнутую поверхность в виде прямого цилиндра с 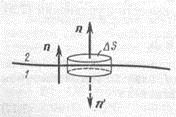 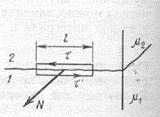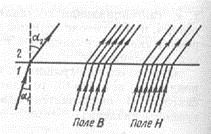(рис.101). Поток вектора магнитной индукции в этом случае:  или  , т. е. нормальная составляющая вектора магнитной индукции одинакова в обоих магнетиках. Так как  , то  .   Рис 101 Рис 102. Рис 103 Применим теорему о циркуляции вектора напряженности к очень малому прямоугольному контуру. Пусть вектор линейной плотности тока совпадает с нормалью к контуру (рис.102). Так как контур очень узкий, то вклад в циркуляцию на боковых сторонах очень мал. Тогда:  или  , т. е. тангенциальная составляющая вектора напряженности, а следовательно и вектора магнитной индукции на границе раздела претерпевает скачок, обусловленный наличием поверхностных токов проводимости.Если на границе раздела магнетиков токов проводимости нет, то  и, соответственно,  . На границе раздела двух магнетиков линии вектора индукции испытывают преломление, но непрерывны  .Линии вектора напряженности преломляются по такому же закону, но терпят разрыв из-за поверхностных токов намагничивания (даже в отсутствие токов проводимости). На рис. 103 представлены линии векторов индукции и напряженности для случая > . На этом основана магнитная защита, т. е. использование замкнутой железной оболочки для защиты внутреннего пространства от внешнего магнитного поля. Линии поля концентрируются в самой оболочке, а в окруженном оболочкой пространстве магнитное поле значительно меньшей величины, чем внешнее поле. 16.3. Типы магнетиков. Вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками. В отсутствии внешнего магнитного поля диамагнетики немагнитны, т.к. у них суммарный магнитный момент атома (молекулы) равен нулю. Диамагнетизм свойственен всем веществам. Диамагнетиками являются висмут, Zn, Au, Ag, H2O, инертные газы, H2, N2 и многие другие элементы и соединения. Наряду с диамагнитными веществами существуют и парамагнитные − вещества, намагничивающиеся во внешнем магнитном поле по направлению поля. У парамагнитных веществ магнитные моменты электронов, входящих в состав атомов (молекул), даже в отсутствии внешнего магнитного полы нескомпенсированы. Вследствие этого атомы (молекулы) парамагнетика обладают собственным магнитным моментом. Однако, из-за теплового движения эти магнитные моменты ориентированы беспорядочно, поэтому в отсутствии внешнего магнитного поля парамагнетики, так же как и диамаг- нетики, немагнитны. При внесении парамагнитного вещества во внешнее магнитное поле магнитные моменты электронов прецессируют относительно направления вектора B (диамагнитное явление), и, в то же время, устанавливается преимущественная ориентация магнитных моментов атомов вдоль поля. Эффект от этого значительно больше, чем от проявления диамагнитных свойств. В итоге индукция магнитного поля в парамагнетике увеличивается. К парамагнетикам относятся щелочные металлы, редкоземельныеэлементы, некоторые газы (Na, K, Al, Pt, O2, NO и др.). Наряду с рассмотренными выше слабомагнитными веществами, существуют еще сильномагнитные вещества − ферромагнетики − вещества, обладающие самопроизвольной (спонтанной) намагниченностью, которая сильно зависит от внешних воздействий − магнитного поля, температуры, деформаций. К ферромагнетикам относятся железо, никель, кобальт, гадолиний, их сплавы и некоторые соединения. 17.1. Ферромагнетизм. Наряду с рассмотренными выше слабомагнитными веществами, существуют еще сильномагнитные вещества − ферромагнетики − вещества, обладающие самопроизвольной (спонтанной) намагниченностью, которая сильно зависит от внешних воздействий − магнитного поля, температуры, деформаций. К ферромагнетикам относятся железо, никель, кобальт, гадолиний, их сплавы и некоторые соединения. 17.2. Кривая намагничивания. Магнитный гистерезис. 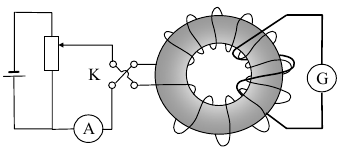 Тороид, первичная обмотка которого состояла из N1 витков, имел сердечник из исследуемого материала (например, железа). Вторичная обмотка из N2 витков была замкнута на баллистический гальванометр G, измеряющих заряд, в прошедшем через него импульсе тока. Первичная обмотка включалась в цепь источника э.д.с., силу тока I в ней I можно было изменять с помощью потенциометра. Направление тока можно изменятькоммутатором К. При изменении направления тока в первичной обмотке с помощью коммутатора на противоположное, в цепи вторичной обмотки возникал импульс индукционного тока, и через баллистический гальванометр проходил электрический заряд q. Как будет показано далее, этот заряд равен отношению взятого с обратным знаком изменения полного магнитного потока сквозь вторичную обмотку к электрическому сопротивлению R цепи гальванометра  где Ф0m − магнитный поток сквозь один виток. Если сердечник тонкий, а площадь его поперечного сечения S, то индукция магнитного поля в сердечнике  Напряженность магнитного поля в сердечнике можно вычислить, используя закон полного тока  где lср − длина средней линии сердечника. Зная В и Н , можно найти намагниченность ферромагнетика  Опыты показали, что для ферромагнетиков наблюдается явление гистерезиса (запаздывание). Суть явления состоит в том, что намагниченность вещества неоднозначно зависит от напряженности магнитного поля. При Н=0 намагниченность J>0, т.е. в ферромагнетике наблюдается остаточная намагниченность Jос, что объясняет существование постоянных магнитов. 17.3. Домены. Спонтанная поляризация является источником очень больших электрических полей. Но с большим электрическим полем связана большая энергия. Известно, что любая система всегда стремится перейти в состояние с наименьшей энергией. Поэтому сегнетоэлектрик переходит в такое состояние, при котором с одной стороны существует спонтанная поляризация, а с другой − энергия его минимальна. Это может осуществиться в результате разделения объема сегнетоэлектрика на малые области в каждой из которых имеется спонтанная поляризация в некотором направлении. Такие области называются диэлектрическими доменами. Из−за хаотичной ориентации спонтанной поляризации отдельных доменов в отсутствии внешнего электрического поля дипольный момент кристалла диэлектрика равен нулю. При наложении электрического поля происходит частичная переориентация доменов, а также рост одних доменов за счет других. 17.4. Точка Кюри. Остаточная намагниченность ферромагнетика может быть нарушена при его сотрясении. Аналогично действует нагревание ферромагнетика. С повышением температуры остаточная намагниченность уменьшается, и при достаточно высокой температуре, называемой точкой Кюри, она исчезает полностью. При температурах выше точки Кюри ферромагнетик ведет себя во внешнем магнитном поле как парамагнитное вещество. 18.1. Явление электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом проводнике при прохождении через него магнитного потока, изменяющегося со временем. То есть благодаря этому явлению мы можем преобразовывать механическую энергию в электрическую, и это замечательно. Ведь до открытия этого явления люди не знали о методах получения электрического тока кроме как от источников тока. Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 году. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого проводящего контура в нем возникает электрический ток, который назвали индукционным током. 18.2. Правило Ленца. Правило Ленца определяет направление индукционного тока и гласит: Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток. 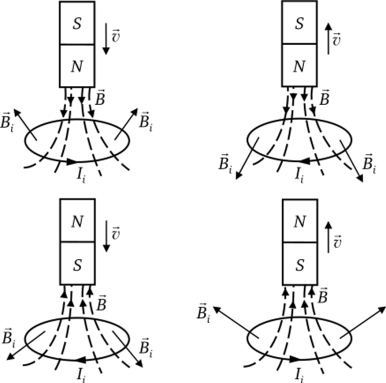 18.3. Закон электромагнитной индукции Фарадея-Максвелла и его вывод.  19.1. Явление самоиндукции. Явление самоиндукции - это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре. 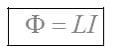  Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре. ЭДС самоиндукции определяется по формуле: 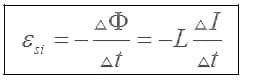  19.2. Индуктивность. Электрический ток во время протекания по контуру образует магнитное поле. Индуктивностью называют способность получать энергию от источника тока и создавать из нее магнитное поле. 19.3. Индуктивность соленоида. Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока Bвнутри катушки является фактически постоянной и (приближенно) равна  Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B, умноженному на площадь поперечного сечения Sи число витков N:  Отсюда следует формула для индуктивности соленоида (без сердечника):  Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель  — относительную магнитную проницаемость сердечника: В случае, когда  , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз. |