Шпаргалка. билеты по физике. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
19.4. Токи при замыкании и размыкании электрических цепей с индуктивностью При всяком изменении силы тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Установление тока при замыкании цепи, а также убывание тока при размыкании цепи происходят не мгновенно, а постепенно и зависят от индуктивности цепи 19.5. Взаимная индуктивность. Взаимоиндукция— явление возникновения ЭДС индукции в одном контуре при изменении силы тока во втором контуре и наоборот. Взаимоиндукция — частный случай электромагнитной индукции. При изменении силы тока в контуре, возникает ЭДС: 19.6. Энергия магнитного поля, плотность энергии магнитного поля. Проводник с электрическим током всегда окружен магнитным полем, а изменение магнитного поля сопровождается возникновением электрического поля. Энергетические превращения свидетельствуют о том, что магнитное поле (как и электрическое) несет энергию. Рассчитаем эту энергию с помощью закона сохранения энергии, примененного для процесса, проиллюстрированного с помощью рис. 24.2. Пусть по катушке индуктивностью L в начальный момент времени течет ток I, возникший благодаря ЭДС. При отключении ЭДС и переводе ключа в другое положение ток поддерживается уже за счет ЭДС самоиндукции, возникающей при уменьшении тока I. Работа, совершаемая ЭДС самоиндукции но перемещению заряда dq, равна Интегрирование по току от начального I до конечного нулевого тока дает полную работу индуктивности: Очевидно, что эта работа совершена за счет магнитного поля соленоида и равна энергии индуктивности: Преобразуем это выражение с учетом формулы (24.13) для индуктивности соленоида и связи (22.21) магнитной индукции внутри соленоида с током: Поскольку магнитное поле соленоида однородно, то, разделив энергию на объем, получим объемную плотность энергии магнитного поля: Плотность энергии магнитного поля измеряется в джоулях на кубический метр. В случае неоднородного ноля плотность энергии магнитного ноля в каждой точке выражается через малый объем dV: При этом энергия поля в объеме V выражается через интеграл по этому объему: 19.7. Энергия катушки с током. Появление мощного тока самоиндукции при размыкании цепи свидетельствует о том, что магнитное поле тока в катушке обладает энергией. Работа по созданию индукционного тока определяется уменьшением энергии магнитного поля. В свою очередь, энергия магнитного поля копится за счёт источника тока при совершении работы по преодолению тока самоиндукции, препятствующего увеличению тока в цепи. Экспериментально выведена формула энергии магнитного поля катушки с током: 20.1. Закон электромагнитной индукции Закон электромагнитной индукции - ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром. 20.2. Первое уравнение Максвелла Первое уравнение Максвелла является обобщением закона полного тока и в дифференциальной форме записывается как 21.1. Ток смещения. При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высоких частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения "прохождения" переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения. Ток смещения существует и в проводниках по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока 21.2. Закон полного тока. Для магнитного поля в вакууме Для произвольной среды 21.3. Второе уравнение Максвелла. Второе уравнение Максвелла является обобщением закона индукции Фарадея и в дифференциальной форме записывается так 22.1. Система уравнений Максвелла для электромагнитного поля в интегральной форме. 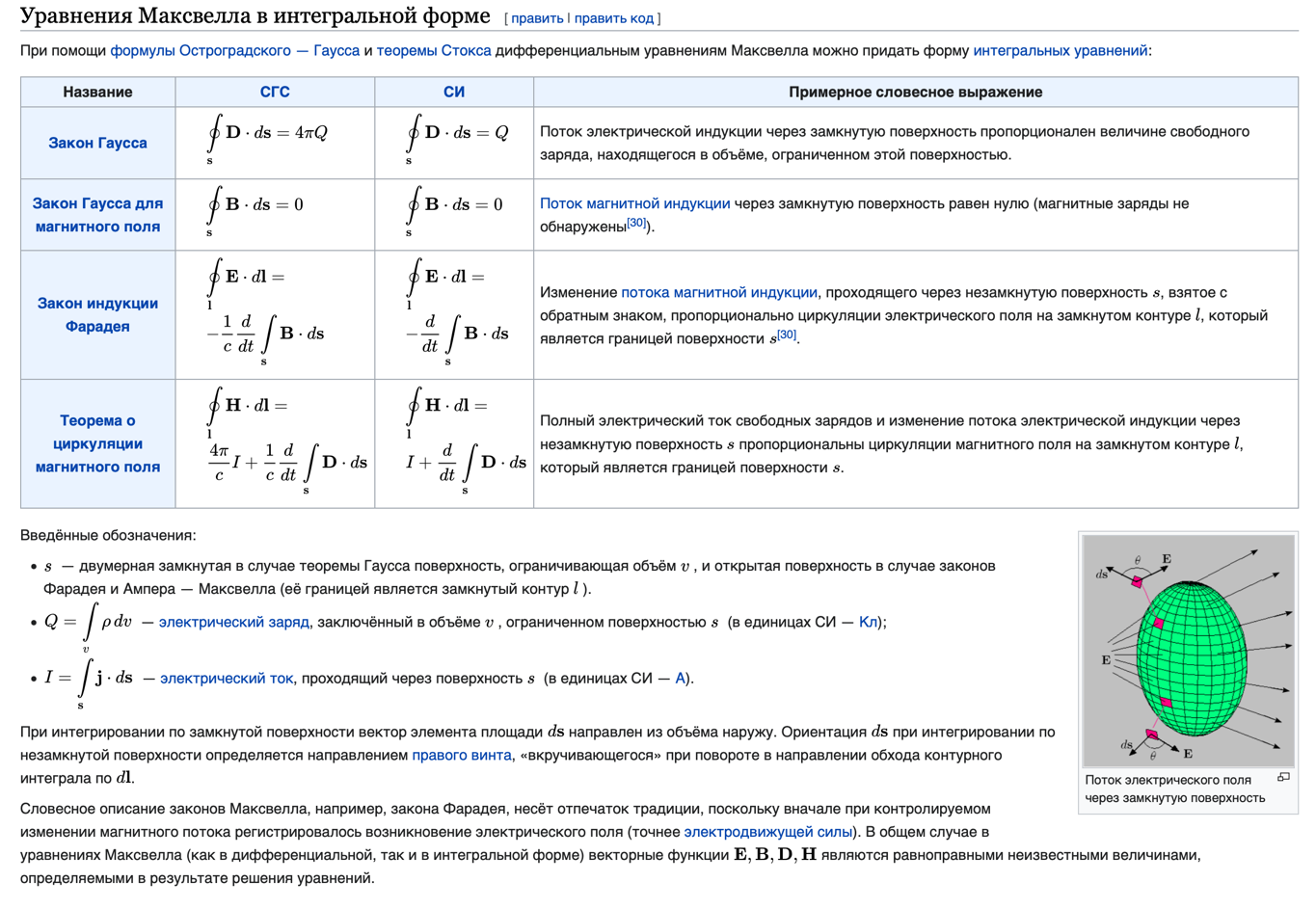 23.1. Гармонические колебания Колебаниями называют процессы, точно или приблизительно повторяющиеся во времени. Если изменения во времени колеблющейся величины происходят по закону синуса или косинуса, то такие колебания называются гармоническими. Они описываются уравнением типа: Величина x называется смещением. Смещение – это координата колеблющейся точки, которую отсчитывают от положения равновесия. Стоящая в скобках величина называется фазой колебаний. Фаза колебаний – это аргумент, функцией которого является состояние колебательной системы в каждый момент времени. Фаза измеряется в угловых единицах – радианах (долях π). Значение фазы в момент t = 0 называется начальной фазой колебаний. Выбор начального момента совершенно произволен. Можно выбрать этот момент так, что начальная фаза будет равна нулю. Поскольку функция косинус изменяется в пределах от -1 до +1, то смещение х может принимать значения − A ≤ x ≤ A . Максимальная величина смещения называется амплитудой. 23.2. Свободные незатухающие гармонические колебания в колебательном контуре. Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t=0 (рис. 19, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 19, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся осла бить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 19, в). Далее те же процессы начнут протекать в обратном направлении (рис. 19, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 19, а). После этого начнется повторение рассмотренного цикла разряд ки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения UC на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение UC на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть : Исходя из того, что UC=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора: или . Решением этого дифференциального уравнения является функция q(t), то естьуравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора: 23.3. Дифференциальное уравнение свободных незатухающих гармонических колебаний и его решение. Решение этого уравнения имеет вид 24.1. Свободные механические колебания. 24.2. Пружинный маятник. Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Период колебаний пружинного маятника может быть вычислен по следующей формуле: 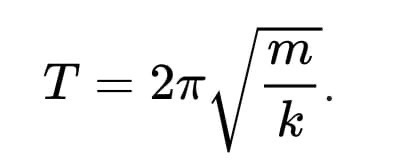 Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей. В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене. Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид: 24.3. Энергия гармонических колебаний. Полная энергия механического движения является суммой кинетической и потенциальной энергий. Кинетическая энергия осциллятора - это энергия движущейся массы Потенциальная энергия в точке x будет равна работе силы, совершаемой при перемещении груза из положения равновесия в данную точку, взятую с обратным знаком. Выражение для полной энергии где 25.1. Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных, примеры) и его решение. решение в случае малых затуханий 25.2. Логарифмический декремент и коэффициент затухания. Количественной мерой затухания колебаний является величина, равная логарифму отношения амплитуд двух последовательных колебаний, отстоящих друг от друга на период Отсюда 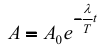 Величина, характеризующая действие силы трения, называется коэффициентом затухания и имеет размерность частоты колебаний. где r - коэффициент трения, зависящий от свойств среды. 25.3. Добротность колебательного контура. Добротность пропорциональна относительному изменению энергии затухающих колебаний за время одного периода колебаний Добротность контура можно определить так 25.4. Апериодический процесс. Период затухающих колебаний равен При очень больших значениях коэффициента затухания ( β > ω0 ) под корнем стоит отрицательная величина. В этом случае частота колебаний становится мнимой, и, несмотря на наличие сил, возвращающих систему в положение равновесия, колебания не возникают. Система возвращается в положение равновесия, асимптотически к нему приближаясь. Такое движение называется апериодическим. 26.1. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. F0 - амплитудное значение вынуждающей силы, ωв — частота внешней силы. Избегая сложных математических выкладок, которые можно почерпнуть в литературе, запишем частное решение (его вещественную часть) уравнения 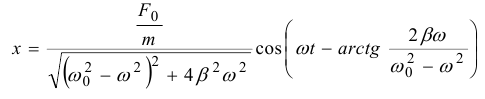 Выражение, стоящее перед функцией косинуса, представляет собой амплитуду вынужденных колебаний. 26.2. Резонанс. Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынужденных колебаний приближается к собственной частоте колебательной системы, называется резонансом. 26.3. Резонансные кривые для напряжения и токов в колебательном контуре. 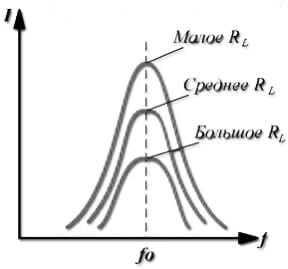 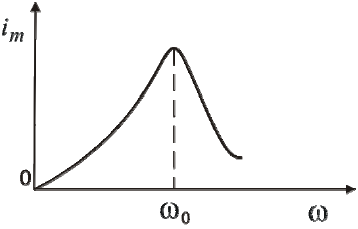 27.1. Сложение гармонических колебаний одного направления и одинаковой частоты. Векторная диаграмма. Биения. Особый практический интерес представляет случай сложения двух гармонических колебаний с близкими амплитудами и мало отличающимися частотами ( ). Примем для простоты начальные фазы равными нулю, тогда x Acos2t, x2 Acos2( )t Складывая x1 и x2 и применяя тригонометрическую формулу для суммы косинусов, получим (с учетом того, что ) xx x 2Acostcos2t. Результирующий процесс можно рассматривать как гармоническое колебание с периодически изменяющейся амплитудой, равной 2Acos()t. Такие колебания называются биениями. Заключенный в скобки множитель (амплитуда биений) в формуле изменяется гораздо медленнее, чем второй множитель. Поэтому результирующее колебание будет почти гармоническим с частотой и периодом T 1 . Амплитуда этого колебания меняется с частотой (частота биений) и периодом: T0 1 . (2) График функции показан на рисунке. График построен для случая 0,1. Частота биений становится тем меньше, чем ближе частоты складываемых колебаний. Это позволяет с большой точностью констатировать равенство частот двух колебаний в момент, когда частота биений падает до нуля. Одним из примеров практического использования метода биений является настройка музыкальных инструментов с помощью камертона. 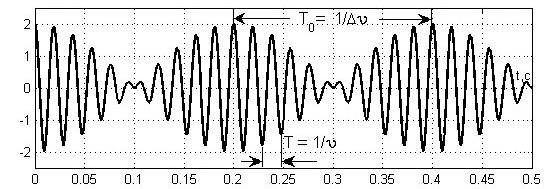 27.2. Сложение взаимно перпендикулярных колебаний. x Acos(2t 1) y Βcos(2t 2) Уравнение описывает эллипс, ориентация и величина полуосей которого зависят от амплитуд A, B и разности фаз (2 1) складываемых колебаний Если частоты взаимно перпендикулярных колебаний неодинаковы, но находятся в кратном отношении, то траектории результирующего движения имеют вид более сложных кривых, называемых фигурами Лиссажу. 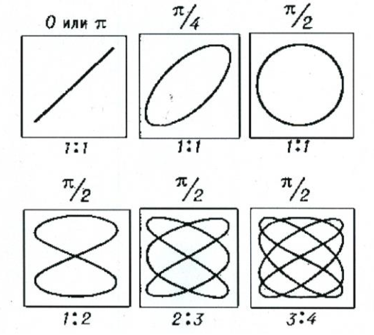  |
