Шпаргалка. билеты по физике. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды

• Название: Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
• Анкор: Шпаргалка
• Дата: 14.06.2022
• Размер: 1.89 Mb.
• Имя файла: билеты по физике.doc
• Тип: Закон; #591438
• страница: 5 из 5

28.1. Механические волны в упругой среде.Продольные и поперечные волны.

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.

28.2. Волновой фронт и волновая поверхность.

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновая поверхность, отделяющая часть пространства, в которой колебания происходят, от той части, где еще нет колебаний, называется фронтом волны. Именно фронт волны перемещается со скоростью равной фазовой скорости волны. В случае одномерной синусоидальной волны уравнение волновой поверхности имеет следующий вид:

Этому условию в каждый момент времени удовлетворяет только одна точка оси ОХ, координата х которой равна:



Различным значениям фазы волны φ соответствуют различные волновые поверхности, каждая из которых в одномерных волнах вырождается в точку. Из последней формулы видно, что волновые поверхности с течением времени перемещаются в среде со скоростью, равной  , т.е. фазовой скоростью, которая равна



Таким образом, для синусоидальной волны скорость распостранения поверхности постоянной фазы совпадает со скоростью распространения волны.

28.3. Уравнение плоской волны.

Плоская волна — волна, поверхность постоянной фазы которой представляет собой плоскость. Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту.



28.4. Длина волны и волновое число.

Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний T[с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны λ [м] можно рассматривать как пространственный период волнового процесса. Следует заметить, что круговой частоте колебания,

ω= 2πf =2π/T

показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» ,

k=2π/λ

называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в λ, отличаются ровно на 2π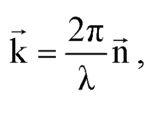

- волновое число

28.6. Волновой вектор.

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.

Наиболее общим определением волнового вектора можно считать такое: волновой вектор есть градиент фазы волны: k=grad ϕ

28.7. Волновое уравнение.

В многомерном случае однородное волновое уравнение записывается в виде Δu=1v2∂2u∂t2



 Используя оператор Лапласа   , волновое уравнение можно записать в виде

29.1. Дифференциальное уравнение электромагнитной волны.

Т 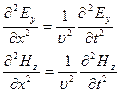аким образом, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т.д. Следовательно, дифференциальные уравнения электромагнитных волн будут иметь вид

Уравнения называются уравнениями плоских монохроматических волн, где Е0у , Н0у – амплитудные значения напряженности электрического и магнитного полей волны.

29.2. Плоская электромагнитная волна.

– Электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют одинаковые напряженности электрических или магнитных полей. 

29.3. Энергия электромагнитной волны. Вектор Умова-Пойнтинга.

Объёмная плотность энергии электромагнитного поля в линейной изотропной среде, как известно из электродинамики, даётся выражением (мы учли здесь также связь между векторами Е и Н в электромагнитной волне):



      Вектор плотности потока энергии электромагнитной волны (то, что в теории упругих волн называется вектором Умова) называется вектором Умова-Пойнтинга, или чаще просто вектором Пойнтинга Р:

        Модуль среднего значения вектора Пойнтинга называется интенсивностью электромагнитной волны: 

        В случае синусоидальной монохроматической плоской (когда плоскости колебаний векторов Е и Н не меняются со временем) электромагнитной волны, распространяющейся в направлении х:

для интенсивности получается:

        Следует обратить внимание, что интенсивность электромагнитной волны зависит от амплитуды (либо электрического, либо магнитного поля; они связаны), но не зависит от частоты волны - в отличие от интенсивности упругих механических волн.