Физика шпоры. Закон Кулона. Закон сохранения электрического заряда. Электрический заряд характеризует способность тел или частиц к электромагнитным взаимодействиям. Еденица электрического заряда Кулон. Кулон
 Скачать 364.74 Kb.
|
30. Уравнение электродинамики Максвелла винтегральной формеПервую пару уравнений Максвелла образуют уравнения  Первое из этих уравнений связывает значения Е с временными изменениями вектора В и является по существу выражением закона электромагнитной индукции. Второе уравнение отражает то свойство вектора В, что его линии замкнуты (или уходят в бесконечность). 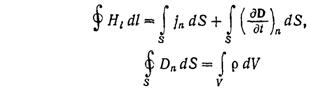 (под j здесь и в дальнейшем понимается плотность тока проводимости). Первое уравнение устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Второе показывает, что линии вектора D могут начинаться и оканчиваться на зарядах. Уравнения (108.1) — (108.4) представляют собой уравнения Максвелла в интегральной форме. Они связывают значения Е или Н вдоль некоторого контура со значениями В (соответственно D) в точках опирающейся на контур поверхности. От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, которые связывают значения Е или Н в некоторой точке с В (соответственно D) в той же самой точке пространства. 31. Энергия электромагнитных волн. Вектор Умова-Пойнтинга Возможность обнаружения электромагнитных волн (по проскакиванию искры, свечению лампочки и т. п.) указывает на то, что эти волны, переносят энергию. Для переноса энергии волной была введена векторная величина, называемая плотностью потока энергии. Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором течет энергия. Направление' вектора плотности потока энергии совпадает с направлением переноса энергии. Там же было показано, что плотность потока энергии можно получить, умножив плотность энергии на скорость волны. Плотность энергии электромагнитного поля w слагается из плотности энергии электрического поля и плотности энергии магнитного поля   32. Электрический колебательный контур. Свободные незатухающие электромагнитные колебания Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным[1]. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона: {\displaystyle f_{0}={1 \over 2\pi {\sqrt {LC}}}.} 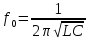 Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания могут быть различными по физической природе (механическими, электромагнитными, гравитационными), но описываются они одинаковыми по структуре уравнениями. Свободные незатухающие, или собственные, колебания – это такие колебания, которые совершаются за счет энергии, сообщенной колебательной системе в начальный момент времени, при отсутствии дальнейшего внешнего воздействия на систему. Дифференциальное уравнение собственных электрических гармонических колебаний LC контура: 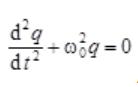 q - электрический заряд конденсатора. W0 - циклическая (круговая) частота свободных незатухающих колебаний.  (здесь L – индуктивность контура; C – электрическая емкость контура).Период свободных незатухающих колебаний в электромагнитном колебательном контуре определяется формулой Томсона^ 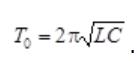 33. Свободные затухающие электромагнитные колебанияСвободные затухающие колебания – это такие колебания, амплитуда которых уменьшается с течением времени вследствие потерь энергии колебательной системой. В электрическом колебательном контуре энергия расходуется на джоулево тепло и на электромагнитное излучение. Мы рассматривали процесс колебаний в контуре без потерь. Однако в реальных контурах всегда происходят необратимые потери энергии на нагрев проводов и диэлектрика, а также на излучение, что приводит к постепенному уменьшению амплитуды электрических колебаний, или, как говорят, к их затуханию. При расчете затухания контура полагают, что он имеет сосредоточенное сопротивление, потребляющее то же количество энергии, которое расходуется в контуре на все виды потерь.  Колебания в контуре затухают тем быстрее, чем большая доля первоначально запасенной в контуре энергии теряется за период колебаний, т. е. чем больше сопротивление потерь по сравнению с его характеристическим сопротивлением. Отношение характеристического сопротивления контура, к сопротивлению потерь называется добротностью: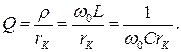 34. Вынужденные электромагнитные колебания. Резонанс Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:  где ε – мгновенное значение ЭДС, εm – амплитудное значение ЭДС. При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления. Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре. |