Физика шпоры. Закон Кулона. Закон сохранения электрического заряда. Электрический заряд характеризует способность тел или частиц к электромагнитным взаимодействиям. Еденица электрического заряда Кулон. Кулон
 Скачать 364.74 Kb.
|
|
| |  , | | |
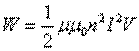а плотность энергии
| |  , | | |
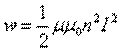Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:
, отсюда 
.Т.к. в вакууме
, имеем
Объемная плотность энергии магнитного поля вычисляется по формуле:
wм=B22μμ0,wм=B22μμ0,
где BB −− магнитная индукция, μμ −− магнитная проницаемость, μ0=4π⋅10−7 Гн/мμ0=4π⋅10−7 Гн/м −−магнитная постоянная.
Формула для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Магнитная энергия локализована в самом магнитном поле.
В однородном магнитном поле в объеме ΔVΔV содержится энергия:
ΔW=wм⋅ΔV.ΔW=wм⋅ΔV.
Энергия произвольного магнитного поля может быть найдена путем интегрирования объемной плотности wэwэ по всему объему, в котором создано магнитное поле.
25. Магнитное поле в веществе. Макро- и микротоки. Магнитные моменты атомов. Намагниченность
Если несущие ток проводники находятся в какой-либо среде, магнитное поле существенным образом изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться).
Намагниченное вещество создает магнитное поле В', которое накладывается на обусловленное токами поле В0. Оба поля в сумме дают результирующее поле:
В=В0+В'.
Макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях и микроскопические токи, обусловленных движением электронов в атомах и молекулах.
Намагниченность постоянных магнитов является следствием существованием в них микротоков.
Внешнее магнитное поле оказывает ориентирующее, упорядочивающее действие на эти микротоки. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции B характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Поэтому, при одном и том же макротоке, вектор B в различных средах будет иметь разные значения. Магнитное поле макротока описывается вектором напряженности магнитного поля H.
В среде магнитное поле макротоков усиливается за счет поля микротоков среды.
Мы уже не раз отмечали, что с механическим моментом атома М связан магнитный момент
. Отношение 
называется гиромагнитным отношением.Хотя представление об орбитах, как и вообще представление о траекториях микрочастиц, является неправомерным, момент, обусловленный движением электронов в атоме, называют орбитальным. Определенное экспериментально отношение магнитного
и механического ML орбитальных моментов совпадает с гиромагнитным отношением, вытекающим из классических представлений Это отношение равно –e/2mec соответственно
(33.1)Величина
называется магнетоном Бора и представляет собой естественную единицу магнитного момента. Знак минус в формуле (33.1) указывает на то, что направления магнитного и механического моментов противоположны (это обусловлено тем, что заряд электрона является отрицательным). Наличие минуса позволяет получить проекцию
на направление z простои заменой в выражении (33.1) 
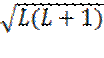на квантовое число mL:
При mL>0 проекция ML положительна, а проекция
отрицательна; при mL26. Закон полного тока в веществе. Магнитная восприимчивость вещества. Магнитная проницаемость среды. Напряженность магнитного поля
Закон полного тока для магнитного поля в вакууме состоит в том, что циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной
на алгебраическую сумму токов, охватываемых этим контуром. Запишем его:
. (5.4)Обобщим закон полного тока на случай магнитного поля в веществе. Для этого нужно учесть все токи, охватываемые контуром: как макротоки (токи проводимости), так и микротоки (молекулярные токи).
Тогда для магнитного поля в веществе имеем:
. (5.5)Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной.
{\displaystyle \chi ={\frac {J}{H}}}
, где {\displaystyle J} — намагниченность вещества под действием магнитного поля, {\displaystyle H} — напряженность магнитного поля.Иногда бывает полезно также ввести понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных килограммах (кг−1). Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль−1).
Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией {\displaystyle {B}}
и напряжённостью магнитного поля {\displaystyle {H}} в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).Впервые встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») в 1881 году[1].
Обычно обозначается греческой буквой {\displaystyle \mu }
. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).27. Типы магнетиков. Диа- и парамагнетики
В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:
1) диамагнетики, у которых х отрицательна и мала по абсолютной величине (ϗкм 10-8
10-7 м3/кмоль),2) парамагнетики, у которых % тоже невелика, но положительна (ϗкм 10-7
10-6 м3/кмоль),3) ферромагнетики, у которых % положительна и достигает очень больших значений (ϗкм 103 м3/кмоль). Кроме того, в отличие oт диа- и парамагнетиков, для которых х постоянна, магнитная восприимчивость ферромагнетиков является функцией напряженности магнитного поля.
Диамагнетиками называются такие вещества, у которых магнитный момент атома в отсутствии внешнего магнитного поля равен нулю.
при 
Парамагнетиками называются вещества, у которых атомы в отсутствии внешнего магнитного поля обладают некоторым постоянным магнитным моментом
при .Однако, вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому
. При наложении магнитного поля возникают силы, ориентирующие магнитные моменты каждого атома. Магнитные моменты стараются выстроиться по полю. Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, сонаправленное с внешним полем и усиливающего его.Процесс ориентации магнитных моментов атомов во внешнем магнитном поле называется парамагнитным эффектом.
В парамагнетике выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стремятся разрушить упорядочение. Поэтому с понижением температуры магнитная восприимчивость парамагнетиков обычно возрастает.
К парамагнетикам относятся: редкоземельные металлы, Pt, Al, Mg, Cr, O2 и др.
28. Ферромагнетики. Домены. Гистерезис. Точка Кюри. Спиновая природа ферромагнетизма
Ферромагне́тики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры(точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Иными словами, ферромагнетик — такое вещество, которое (при температуре ниже точки Кюри) способно обладать намагниченностью в отсутствии внешнего магнитного поля.
Домен— область вферромагнитном кристалле, в которой существует самопроизвольная намагниченность при температуре ниже температуры Кюри. Аналогичные домены существуют также всегнетоэлектрическихк ристаллах и других веществах, обладающих спонтанным дальним порядком.
хранение данных на жестких дисках осуществляется с использованием горизонтально или вертикально расположенных магнитных доменов;
магнитные домены, перемещаемые по специальных трекам, могут быть использованы при создании перспективной трековой памяти [1].
То́чка Кюри́, или температу́ра Кюри́, — температура фазового перехода II рода, связанного со скачкообразным изменением свойств симметрии вещества (например, магнитной — в ферромагнетиках, электрической — в сегнетоэлектриках, кристаллохимической — в упорядоченных сплавах). Названа по имени П. Кюри[1].
Гистере́зис (греч. ὑστέρησις — «отстающий») — свойство систем (обычно физических), которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть поведение системы зависит от её собственной истории. Не следует путать это понятие с инерционностью поведения систем, которое обозначает стабильное сопротивление системы изменению её состояния.
Магнитный гистерезис— явление зависимостивектора намагничиванияи векторанапряженности магнитного поляв веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется вферромагнетиках—Fe,Co,Niи сплавах на их основе. Именно магнитным гистерезисом объясняется существованиепостоянных магнитов.
29. Ток смещения
Для установления количественных соотношений между изменяющимся электрическим и возникающим магнитным полями Максвелл ввел в рассмотрение так называемый ток смещения. Рассмотрим цепь квази-стационарного переменного тока, содержащую конденсатор (рис.
228). Движение свободных носителей заряда, т. е. ток проводимости, имеет место "во всей цепи, кроме зазора между обкладками конденсатора. Следовательно, линии тока проводимости терпят на границах обкладок разрыв. Зато в пространстве между обкладками имеется переменное электрическое поле, которое можно охарактеризовать смещением D. Максвелл предположил, что линии тока проводимости непрерывно переходят на границе обкладок в линии тока, названного им током смещения.
Мгновенное значение силы тока равно i = q. Плотность тока проводимости в непосредственной близости от поверхности обкладок определяется выражением
де S — площадь обкладки, q — распределенный на ней заряд,
— поверхностная плотность заряда.
Чтобы линии тока смещения имели такую же густоту, как и линии тока проводимости, плотность тока смещения jсм также должна быть равна
.D=
Откудаjcм=
Ток смещения имеется везде, где есть изменяющееся электрическое поле. Следовательно, он существует и внутри проводника, по которому течет переменный электрический ток. Однако внутри проводов jсм обычно бывает пренебрежимо мал по сравнению с jпр.