Физика шпоры. Закон Кулона. Закон сохранения электрического заряда. Электрический заряд характеризует способность тел или частиц к электромагнитным взаимодействиям. Еденица электрического заряда Кулон. Кулон
 Скачать 364.74 Kb.
|
18. Действие магнитного поля на движущийся заряд. Сила ЛоренцаЭлектрический ток представляет собой совокупность упорядоченно движущихся заряженные частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Проводник, по которому течет ток, отличается от проводника без тока лишь тем, что в нем происходит упорядоченное движение носителей заряда. Отсюда вывод, что сила, действующая на проводник с. током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, а уже от этих зарядов действие передается проводнику, по которому они перемещаются. Согласно на элемент тока dI действует в магнитном поле сила df=i[dlB] Заменив idl через Sj. dl , выражению закона Ампера можно придать вид df=Sdl [jB] = [jB] dV, где dV — объем проводника, к которому приложена сила dt. Разделив df на dV, получим «плотность силы», т. е. силу, действующую на единицу объема проводника: fуд.об. = [jB] Подставив в эту формулу выражение для j, найдем, что fуд.об.=ne’[uB] Эта сила равна сумме сил, приложенных к носителям, заключенным в единице объема. Таких носителей n, следовательно, на один носитель действует сила, равная fуд.об./n = e’[uB]. Таким образом, можно утверждать, что на заряд е', движущийся со скоростью v в магнитном поле В, действует сила f=e'[vB] называют силой Лоренца или лоренцевой силой. Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы v и В. Если заряд е' положителен, направление силы совпадает с на правлением вектора [vB], В случае отрицательного е' направления векторов f и [vB] противоположны. 19. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора магнитной индукции) Возьмем контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В:  В начале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор  направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности).Воспользуемся свойствами скалярного произведения векторов.  где  – проекция dl на вектор , но  , где R – расстояние от прямой тока I до dl. .Отсюда
это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9). При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому  , и следовательно
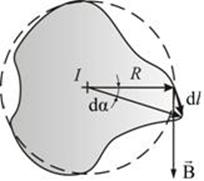 Рис. 2.9 Итак,  , где I – ток, охваченный контуром L.Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы. Если контур охватывает несколько токов, то
т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.Теорема о циркуляции вектора индукции магнитного поля  позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10):  . Рис. 2.10 Итак, циркуляция вектора магнитной индукции отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора  :  ).Такие поля, называются вихревыми или соленоидальными. |
,
,
,