Материалы для подготовки к экзамену по электротехнике. Закон Ома. Работа и мощность в электрической цепи. Закон ДжоуляЛенца
 Скачать 2.39 Mb. Скачать 2.39 Mb.
|
|
1. Абсолютная погрешность ΔА – это разность между измеренным значением электрической величины АИ и ее действительным значением АД : ΔА = АИ – АД [А; В; Вт] Действительное значение измеряемой электрической величины (тока, напряжения, мощности) всегда неизвестно, поэтому его можно определить только приблизительно: 1.1. В случае единичного измерения - по показанию АЭ эталонного прибора , т.е. принять АД = АЭ . 1.2. В случае нескольких измерений – как среднее арифметическое значение из результатов этих измерений АД = А СР . 1.3. В случае единичного измерения и при отсутствии эталонного ЭИП абсолютную погрешность измерения можно вычислить по классу точности (Кл), указанному на шкале рабочего ЭИП, и известному пределу измерения AH : ΔА = (AH * Кл ) / 100 [А; В; Вт]. 2. Относительная погрешность δ - это выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой электрической величины : δ = (ΔА / АД ) * 100 [%] . Поскольку АД = АИ + ΔА , то для относительной погрешности измерения можно записать: δ = (AH * Кл ) / АИ + ΔА = Кл / [(АИ / АН ) + (Кл /100)]. При использовании ЭИП даже среднего класса точности 0,5 - 1,0 и при условии, что измеряемая величина АИ близка к пределу измерения АН величиной (Кл /100) можно пренебречь и тогда для расчёта относительной погрешности измерения можно использовать формулу: δ = (Кл * AH ) / АИ [%]. Другими словами можно считать, что при правильном выполнении условий проведения измерений на ЭИП различие между измеренным и действительным значениями электрической величины достаточно мало и для расчёта относительной погрешности измерения можно использовать приведённую выше формулу: δ = (AH * Кл ) / АИ [%] . 3. Приведенная погрешность γ – это отношение абсолютной погрешности к номинальному значению (пределу измерения) ЭИП, выраженное в процентах: γ = (ΔА / AH ) *100 [%] . Особенности работы с многопредельными приборами. В общем случае для обеспечения более высокой точности измерений из нескольких имеющихся ЭИП (или из пределов многопредельного прибора) следует выбрать прибор с минимальной относительной погрешностью d по условию: d = Кл * АН / АИ = min , где Кл - класс точности измерительного прибора ( % ), АИ - заданное (выбранное или предполагаемое, оценочное) значение измеряемой величины. Из этого условия следует, что с целью снижения погрешности измерений в случае ЭИП с одинаковым классом точности выбирают прибор, предел измерения которого АН является большим ближайшим значением к измеряемой величине АИ . Другими словами выбирают прибор с пределом измерения АН ближайшим большим к измеряемой величине АИ (заданной или предполагаемой) т.е. так, чтобы показания прибора находились в конце шкалы, где относительная погрешность измерения d снижается и приближается к классу точности ЭИП. Из формулы d = Кл * АН / АИ следует, что при АИ ≈ АН d ≈ Кл = min . 6. Переменный электрический ток. Способы представления синусоидальных величин. Основные характеристики переменного тока. Период, частота, начальная фаза, сдвиг фаз, действующее значение переменного тока. Переменный электрический ток - это электрический ток, величина и направление которого во времени изменяется по синусоидальному закону. Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надёжностью их работы и удобством в эксплуатации. В промышленных масштабах переменный ток получают централизованно на электростанциях с помощью электромашинных устройств - синхронных генераторов. Переменный ток и его характеристики (параметры) могут быть представлены одним из следующих способов: 1. Алгебраический: i = ImSin( ωt +Ψi); u = UmSin( ωt +Ψu) 2. В виде волновой диаграммы (осциллограммы): 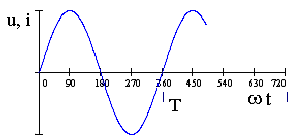 3. В комплексной форме: Ī m = I m e j ( ωt+Ψ i ) ; Ī m = I m Ūm = Um e j ( ωt+Ψ u ) ; Ūm = Um 4. В виде векторной диаграммы: 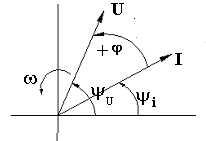 Основные характеристики (параметры) переменного тока Переменные синусоидальные напряжение и ток обычно представляют в алгебраической форме в виде записи:i = ImSin( ωt + Ψi) u = Um · Sin( ωt +Ψu ) , где i , u – мгновенные значения функции, Im , Um , – амплитудные значения функции, ( ωt +Ψi ) – аргумент или фаза функции, Ψi , Ψu – начальные фаз, Т [с] - период - длительность полного цикла изменения синусоидальной величины. ω = 2πf [рад/с] - угловая частота - скорость изменения аргумента функции, f =1 /Т [с-1] или [Гц] - циклическая частота - число периодов в единицу времени (промышленная частота f= 50 Гц), Начальная фаза функции – Ψi, и, е – это значение аргумента функции в нулевой момент времени (t = 0). Сдвиг фаз (в электротехнике) – это разность начальных фаз напряжений и тока : φ= Ψи – Ψi . Величина и знак сдвига фаз не зависит от выбора момента времени, а определяется характером электрической цепи (активным, индуктивным, ёмкостным или смешанным). Действующее значение переменного тока Для сравнения теплового, механического и др. эффектов действия переменного и постоянного тока вводится понятие - действующее значение переменного тока ( I ) (а также напряжения - U и ЭДС - E ). Из условия равенства тепловыделения при протекании постоянного и переменного тока получены следующие соотношения между действующими и амплитудными значениями синусоидальных величин: I = I m / Действующее значение переменного тока (напряжения, ЭДС) меньше амплитудного значения в 7. Метод векторных диаграмм. Основные характеристики переменного тока. Применение комплексного метода для анализа электрических цепей переменного тока (алгебраическая, тригонометрическая и показательная форма). В электротехнике переменного тока для расчета и анализа электрических цепей широко используются так называемые векторные диаграммы. Метод векторных диаграмм основан на том, что любая электрическая синусоидальная величина (i, u, e) может быть представлена на плоскости в виде векторной диаграммы, т.е. в виде вращающегося против часовой стрелки радиус-вектора, модуль которого равен амплитуде функции, а угловая скорость ω равна угловой частоте функции (ω = 2π f). 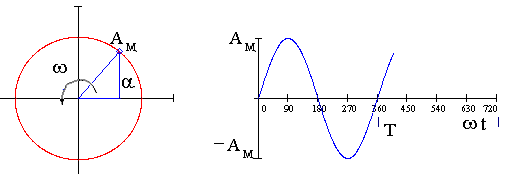 1. Мгновенное значение - (i, u, e) на векторной диаграмме определяется как проекция радиус-вектора на ось ординат. 2. Начальная фаза - Ψ на векторной диаграмме определяется углом между радиус-вектором и осью абсцисс. 3. Сдвиг фаз - на векторной диаграмме определяется углом между векторами напряженияU и тока I . Применение комплексных чисел для анализа цепей переменного тока Комплексное число – это сумма действительного и мнимого чисел, например, Ā = а + jb, где a и b - действительные числа, j = На комплексной плоскости в координатах (+1 , +j ) комплексное число Ā может быть представлено либо точкой с координатами ( a , b), либо вектором Ā, проведенным из начала координат в эту точку, и фазовым углом α . 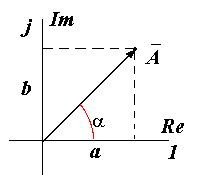 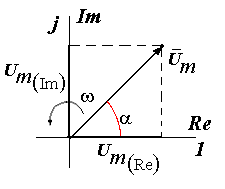 В электротехнике любая синусоидальная величина (i, u, e) может быть представлена на комплексной плоскости в виде вращающегося против часовой стрелки вектора, например, напряжения Ūm. В электротехнике любая синусоидальная величина (i, u, e) может быть представлена на комплексной плоскости в виде вращающегося против часовой стрелки вектора, например, напряжения Ūm. Для удобства расчетов в электротехнике используют различные формы представления электрических величин в комплексном виде: 1. Алгебраическая форма: Ūm= Um( R e) + jUm( Im ); - удобна при сложении и вычитании комплексных величин. 2. Тригонометрическая форма: Ūm = UmCos ( ωt +Ψu)+ jUmSin ( ωt +Ψu) ; - используется для перехода от алгебраической формы записи к операторной и наоборот. 3. Операторная или показательная форма основана на использовании формулы Эйлера Cosα + jSinα = ejα иудобна при умножении и делении комплексных величин: Ūm = Umej (ωt + Ψu ). В качестве характеристики (параметра) элемента (участка) электрической цепи вводится понятие – комплексное сопротивление: или в тригонометрической форме : Z Cos = R - действительная составляющая комплексного сопротивления называется активным сопротивлением, Z Sin = Х - мнимая составляющая комплексного сопротивления называется реактивным сопротивлением. 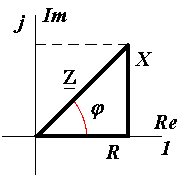 Комплексное сопротивление элемента (участка) электрической цепи можно представить в алгебраической форме: Комплексное сопротивление элемента (участка) электрической цепи можно представить в алгебраической форме: 8. Электрическая цепь переменного тока. Характеристики идеальных и реальных элементов цепи переменного тока. Условно-графические обозначения. Понятие об активной, реактивной и полной мощностях. Понятие об активной, реактивной и полной мощностях. В цепях переменного тока в связи с периодическим изменением электрического тока энергия электрических и магнитных полей периодически изменяется и между этими полями и источником электрической энергии происходит обратимый периодический процесс обмена электрической энергией. Скорость такого обратимого процесса обмена электрической энергией между источником и электрической цепью характеризуется понятием реактивная мощность Q[ ВАр], (Вольт-Ампер реактивный). Одновременно в электрической цепи переменного тока происходит необратимый процесс преобразования электрической энергии в тепло, свет и другие виды энергии, т.е. в работу. Скорость такого необратимого процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт], (Ватт). Таким образом, в общем случае в цепи переменного тока одновременно происходят два процесса: процесс преобразования электрической энергии в другие виды (в работу) и процесс обратимого периодического обмена энергией между источником и цепью. Эти два одновременно протекающих процесса, накладываясь друг на друга, создают в цепи сложный единый энергетический процесс, для характеристики которого вводится понятие полная мощность S[ВА], (Вольт-Ампер). 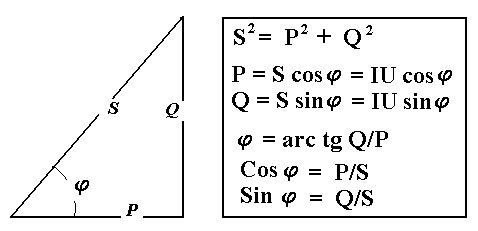 Полученные энергетические соотношения могут быть условно представлены на плоскости в геометрической форме - в виде прямоугольного треугольника - треугольника мощностей, из которого могут быть получены дополнительные формулы, необходимые для выполнения электротехнических расчетов. Полученные энергетические соотношения могут быть условно представлены на плоскости в геометрической форме - в виде прямоугольного треугольника - треугольника мощностей, из которого могут быть получены дополнительные формулы, необходимые для выполнения электротехнических расчетов. Для удобства анализа работы и расчета цепей переменного тока вводят упрощения и используют условные идеализированные электрические схемы – схемы замещения,которые составляют из так называемых идеальных электрических элементов и которые с достаточным для практических целей приближением отображают электрофизические закономерности реальной электрической цепи. Идеальный электрический элемент - это участок условной идеальной электрической цепи (схемы замещения), выделенный условно-графическим обозначением (УГО) и буквенно-цифровым обозначением (БЦО), в котором происходит только один энергетический процесс. Для раздельного отображения процессов преобразования и обмена электрической энергией на электрической схеме замещения используются активный и реактивный элементы. Активный (резистивный) R- элемент (идеальный резистор) - это элемент схемы замещения, в котором происходит процесс необратимого преобразования электрической энергии в другие виды, т.е. в работу как полезную, так и включающую различного рода потери. В активном элементе по определению отсутствуют переменные электромагнитные поля, поэтому в нем не происходит обмена электрической энергией. Скорость процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт].  R [Ом] - сопротивление активного (резистивного) элемента (активное сопротивление). R [Ом] - сопротивление активного (резистивного) элемента (активное сопротивление).Реактивный Х- элемент- это элемент схемы замещения, в котором происходит процесс обратимого периодического обмена электрической энергии между электрическим полем (ёмкостный элемент) и переменным магнитным полем (индуктивный элемент). Реактивные элементы (ёмкостный и индуктивный) можно рассматривать как аккумуляторы электрической энергии, которая запасается в них в виде энергии электрического или магнитного поля. Скорость периодического процесса обмена электрической энергией между электромагнитными полями характеризуется понятием реактивная мощность Q[ВАр]. Индуктивный L - элемент (идеальная катушка) обладает свойствомпериодически запасать электрическую энергию в виде энергии переменного магнитного поля и характеризуется понятием индуктивность: L = ddi [Гн] , где: w магнитное потокосцепление катушки, w - число витков обмотки, - магнитный поток катушки. Преобразования электрической энергии в индуктивном элементе не происходит Р = 0, поэтому индуктивный элемент активным сопротивлением не обладает, т. е. R = 0. Ёмкостный С - элемент (идеальный конденсатор) обладает свойствомпериодически запасать электрическую энергию в виде энергии переменного электрического поля и характеризуется понятием ёмкость: С = dq/ du [Фарада],[Ф], где: q - электрический заряд конденсатора, u – напряжение на зажимах конденсатора. 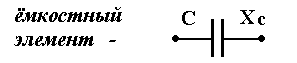 X C [Ом] - сопротивление ёмкостного элемента (ёмкостное сопротивление). Преобразования электрической энергии в ёмкостном элементе (по определению) не происходит Р = 0 , поэтому ёмкостный элемент (идеальный конденсатор) активным (резистивным) сопротивлением не обладает, т. е. R = 0. В общем случае в любом реальном электротехническом устройстве - потребителе электрической энергии (Z), включенном в сеть переменного тока, одновременно происходят оба энергетических процесса - преобразование и периодический обмен электрической энергии. Поэтому такой реальный элемент Z на схеме замещения можно представить как комбинированный, т.е. состоящий из двух идеальных элементов: активного - R и реактивного – Х (индуктивного - L или ёмкостного – C ). Реальный элемент: Z [ R , X ] Z { R , L } или Z { R , C }. Для характеристики любого реального элемента цепи переменного тока обычно используют такие параметры как: R [Ом], L [Гн] или X L [Ом], С [Ф] или Х С [Ом]. Таким образом, схема замещения реальной цепи переменного тока может характеризоваться либо одним параметром (R, L, C) в случае идеализированной реальной цепи, либо комбинацией этих параметров при различных способах соединения резистивного R и реактивного Х элементов. 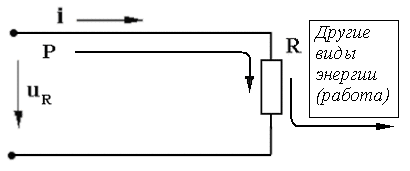 9. Идеальные элементы (резистивный, индуктивный и емкостный) в цепи переменного тока. Определения, основные соотношения и особенности цепи. Понятие об активной, реактивной и полной мощностях. 9. Идеальные элементы (резистивный, индуктивный и емкостный) в цепи переменного тока. Определения, основные соотношения и особенности цепи. Понятие об активной, реактивной и полной мощностях.
Резистивный элемент R , обладающий активным сопротивлением R [Ом], включен в сеть переменного тока i = ImSinωtна напряжение uRи потребляет от питающей сети некоторую мощность Р [Вт], которая преобразуется в другие виды энергии, т.е. в некоторую работу. Поскольку в резистивном элементе по определению отсутствуют переменные электромагнитные поля то по закону Ома для участка цепи сила тока i = uR / R . Тогда:  Разделив обе части этого выражения на  или в комплексной форме: или в комплексной форме: Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей резистивный элемент (или другими словами – в резистивном элементе), сдвиг фаз φR = Ψи - Ψi = 0, т.е. напряжение и ток в резистивном (активном) элементе совпадают по фазе или синфазны. 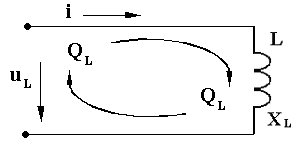 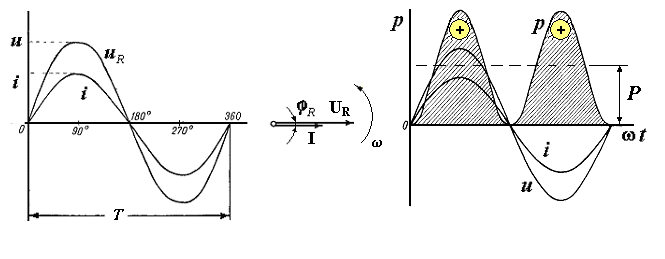 В резистивной цепи коэффициент мощности CosφR = 1, поэтому среднее значение электрической мощности за период или активная мощность в резистивной цепи равна полной мощности: Р = Pcp = IUCosφR = IU = S- резистивная цепь потребляет от сети только активную мощность P = S. Реактивная (обменная) мощность в резистивной цепи: Q = IUSinφR = 0 - в резистивной цепи отсутствует обмен реактивной энергией Q = 0. 2. Индуктивный элемент в цепи переменного тока Индуктивный элемент L [Гн] (идеальная катушка) включен в сеть переменного тока i = ImSinωtна напряжение uLиучаствует в обмене реактивной энергией QL [ВАр] с питающей сетью. Идеальная катушка (по определению) не имеет активного сопротивления R = 0 и в ней не происходит преобразования электрической энергии Р = 0. При этом такая катушка обладает свойствомпериодически запасать электрическую энергию в виде энергии переменного магнитного поля QLи обмениваться ею с источником. Поскольку магнитное поле является переменным, то при его изменении в обмотке катушки будет наводиться переменная ЭДС самоиндукции: eL = - ddt = - Ldi /dt[В], где L = ddi[Гн] - индуктивность катушки. По второму правилу Кирхгофа для такой цепи можно записать: uL + eL) =iR = 0 uL + eLuL = - eL = Ldi /dt. После подстановки получаем выражение для мгновенного значения индуктивного напряжения uL: Отсюда получаем выражение закона Ома для амплитудных значений: Разделив обе части этого выражения на В таком случае закон Ома для индуктивной цепи можно записать: Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей индуктивный элемент (или другими словами – в индуктивном элементе), сдвиг фаз φL = Ψи - Ψi = + 90 O, т.е. напряжение в индуктивном элементе опережает по фазе ток на четверть периода ( +/2 или + 90 O), а ЭДС находится в противофазе с индуктивным напряжением. 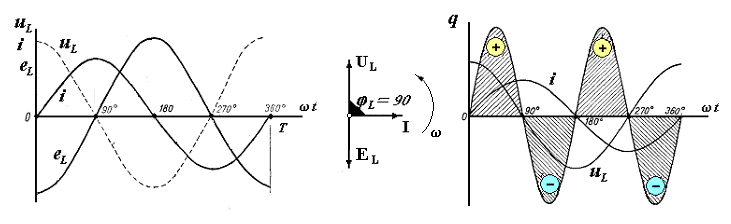 В индуктивной цепи коэффициент мощности CosφL = 0 , поэтому среднее значение электрической мощности за период или активная мощность равна нулю: Р = IUCosφL =0- индуктивная цепь не потребляет от сети активную мощность, следовательно, в ней не происходит преобразования электрической энергии в работу. Реактивная (обменная) мощность в индуктивной цепи (индуктивная мощность) равна полной мощности: QL = IUSinφL = IU = S- индуктивная цепь потребляет от сети только реактивную мощность QL = S.
Идеальный конденсатор (по определению) не имеет активного сопротивления R = 0 и в нем не происходит преобразования электрической энергии Р = 0. При этом такой конденсатор обладает свойствомпериодически запасать электрическую энергию в виде энергии переменного электрического поля QCи обмениваться ею с источником. Из выражения для ёмкости  можно записать: можно записать: где  - амплитуда ёмкостного напряжения. - амплитуда ёмкостного напряжения.Отсюда получаем выражение закона Ома для амплитудных значений: Разделив обе части этого выражения на  - имеет размерность сопротивления [Ом] и называется ёмкостным сопротивлением. - имеет размерность сопротивления [Ом] и называется ёмкостным сопротивлением. В таком случае закон Ома для ёмкостной цепи можно записать:  Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей ёмкостный элемент (или другими словами – в ёмкостном элементе), сдвиг фаз φС = Ψи - Ψi = - 90 O, т.е. напряжение в ёмкостном элементе отстает по фазе от тока на четверть периода ( -пи /2 или - 90 O). 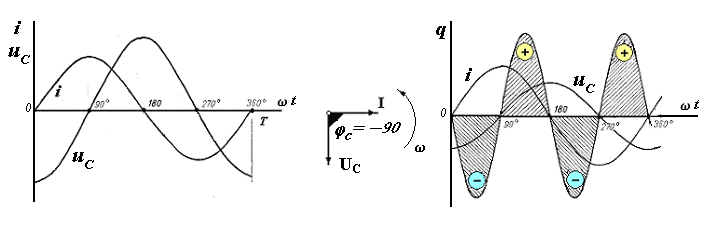 В ёмкостной цепи коэффициент мощности CosφС = 0 , поэтому среднее значение электрической мощности за период или активная мощность равна нулю: Р = IUCosφС = 0 -ёмкостная цепь не потребляет от сети активную мощность, следовательно, в ней не происходит преобразования электрической энергии в работу. Реактивная (обменная) мощность в ёмкостной цепи (ёмкостная мощность) равна полной мощности: QС = IUSinφС = IU = S - ёмкостная цепь потребляет от сети только реактивную мощность QС = S. Понятие об активной, реактивной и полной мощностях. |

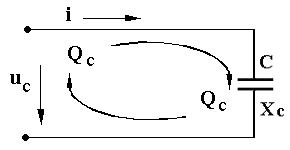 сетью.
сетью.