Материалы для подготовки к экзамену по электротехнике. Закон Ома. Работа и мощность в электрической цепи. Закон ДжоуляЛенца
 Скачать 2.39 Mb.
|
|
В цепях переменного тока в связи с периодическим изменением электрического тока энергия электрических и магнитных полей периодически изменяется и между этими полями и источником электрической энергии происходит обратимый периодический процесс обмена электрической энергией. Скорость такого обратимого процесса обмена электрической энергией между источником и электрической цепью характеризуется понятием реактивная мощность Q[ ВАр], (Вольт-Ампер реактивный). Одновременно в электрической цепи переменного тока происходит необратимый процесс преобразования электрической энергии в тепло, свет и другие виды энергии, т.е. в работу. Скорость такого необратимого процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт], (Ватт). Таким образом, в общем случае в цепи переменного тока одновременно происходят два процесса: процесс преобразования электрической энергии в другие виды (в работу) и процесс обратимого периодического обмена энергией между источником и цепью. Эти два одновременно протекающих процесса, накладываясь друг на друга, создают в цепи сложный единый энергетический процесс, для характеристики которого вводится понятие полная мощность S[ВА], (Вольт-Ампер). 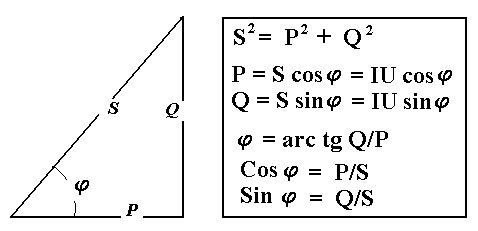 Полученные энергетические соотношения могут быть условно представлены на плоскости в геометрической форме - в виде прямоугольного треугольника - треугольника мощностей, из которого могут быть получены дополнительные формулы, необходимые для выполнения электротехнических расчетов. 10. Реальная катушка и реальный конденсатор в цепи переменного тока. Определения, основные соотношения и особенности цепи. Понятие об активной, реактивной и полной мощностях. Любой промышленный или бытовой потребитель электрической энергии, т.е. элемент реальной электрической цепи переменного тока, в котором происходят два энергетических процесса - преобразования и периодического обмена электрической энергии,может быть представлен на электрической схеме замещения в виде так называемого реального элемента Z. В отличие от идеальных элементов (активного R и реактивного Х), в которых по определению происходит только один энергетический процесс (преобразования или обмена электрической энергией), в реальном элементе происходят одновременно оба энергетических процесса. Поэтому такой реальный элемент Z на схеме замещения можно представить как комбинированный, т.е. состоящий из двух идеальных элементов: активного - R и реактивного – Х (индуктивного - L или ёмкостного – C ). Реальный элемент: Z [ R , X ] Z { R , L } - катушка, (реальная катушка с тепловыми потерями), Z { R , C } - конденсатор, (реальный конденсатор с тепловыми потерями). - катушка (реальная катушка с тепловыми потерями): 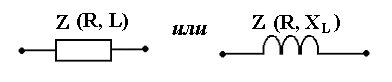 - конденсатор (реальный конденсатор с тепловыми потерями): 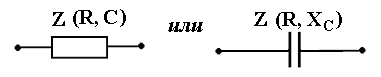 1. Катушка (активно-индуктивный R- L элемент) в цепи переменного тока 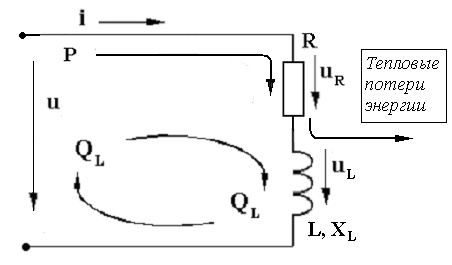 Реальная катушка Z наряду с индуктивностью L [Гн], связанной с наличием переменного магнитного поля в катушке, обладает активным сопротивлением R , обусловленным сопротивлением провода, из которого изготовлена катушка: R = ρ l /S[Ом].На этом сопротивлениив катушке происходят тепловые потери электрической энергии Р = I 2 R [Вт] (так называемые “джоулевы потери”), поэтому такая катушка на схеме замещения может быть представлена в виде последовательного, а иногда параллельного, соединения активного R и индуктивного L идеальных элементов: При включении активно-индуктивной цепи в сеть переменного тока на напряжение uв ней протекает ток i = ImSinωtи по второму правилу Кирхгофа для мгновенных значений напряжений можно записать:u=uR + uL , - или, переходя к действующим значениям напряжений, можно записать в векторной форме:  , U - напряжение на зажимах питающей сети (напряжение цепи),- U R = I R - напряжение на активном элементе (активная составляющая) - U L = I X L - напряжение на индуктивном элементе (индуктивная составляющая) Полученные соотношения можно представить на плоскости в виде векторной диаграммы: 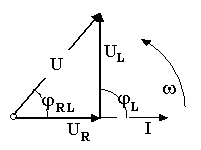 Векторы напряжений U, U R = I Rи U L = I X L образуют прямоугольный треугольник напряжений, поэтому можно записать:U 2 = (I R)2 + (I X L)2 или  откуда получаем выражение закона Ома для активно-индуктивной (R-L) цепи переменного тока:  -здесь  - полное сопротивление активно-индуктивной (R- L) цепи.Из треугольника напряжений можно получить скалярные прямоугольные треугольники - треугольник сопротивлений (если стороны треугольника напряжений разделить на силу тока I) и треугольник мощностей (если стороны треугольника напряжений умножить на силу тока I). Из этих треугольников можно получить дополнительные количественные соотношения, необходимые для расчета электрической цепи: 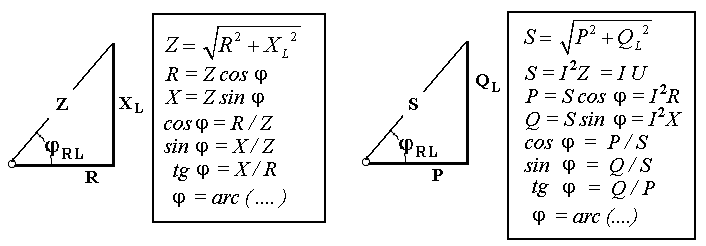  2. Конденсатор (активно-ёмкостный R- С элемент) в цепи переменного токаВ конденсаторе с идеальным диэлектриком (идеальный конденсатор) предполагается полное отсутствие тока проводимости и тепловых потерь электрической энергии. В реальном же конденсаторе в отличие от идеального существуют тепловые потери ∆P [Вт], поэтому такой конденсатор может быть представлен на схеме замещения в виде последовательного, а иногда параллельного, соединения активного элемента R , учитывающего тепловые потери в диэлектрике (т.е. нагрев конденсатора - R = ∆P/ I 2 ) и ёмкостного элемента (ёмкости) С [Ф] , связанной с наличием переменного электрического поля в конденсаторе. 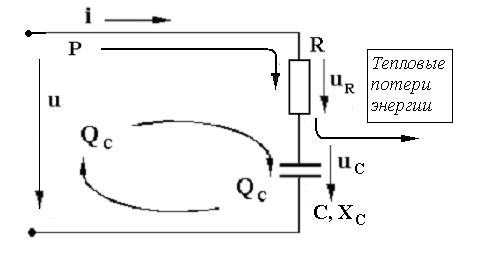 При включении активно-ёмкостной цепи в сеть переменного тока на напряжение uв ней протекает ток i = ImSinωtи по второму правилу Кирхгофа для мгновенных значений напряжений можно записать: u = uR + uС , - или, переходя к действующим значениям напряжений, можно записать в векторной форме:  , U-напряжение на зажимах питающей сети (напряжение цепи),- U R = I R - напряжение на активном элементе (активная составляющая), - U С = I X С - напряжение на ёмкостном элементе (ёмкостная составляющая напряжения цепи Uили ёмкостное напряжение) отстает по фазе от тока. Полученные соотношения можно представить на плоскости в виде векторной диаграммы: 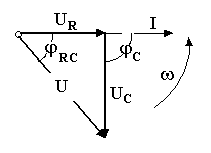 Векторы напряжений U, U R = I Rи U С = I X С образуют прямоугольный треугольник напряжений , поэтому можно записать: U 2 = (I R)2 + (I X С)2 или  --откуда получаем выражение закона Ома для активно-ёмкостной (R- С) цепи переменного тока:  , здесь  - полное сопротивление активно-ёмкостной (R- С) цепи.Из треугольника напряжений можно получить скалярные прямоугольные треугольники - треугольник сопротивлений (если стороны треугольника напряжений разделить на силу тока I) и треугольник мощностей (если стороны треугольника напряжений умножить на силу тока I). Из этих треугольников можно получить дополнительные количественные соотношения, необходимые для расчета электрической цепи: 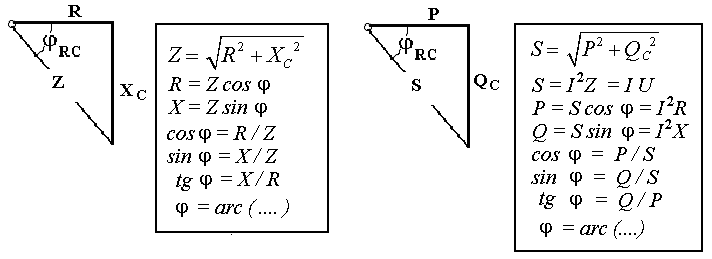 Понятие об активной, реактивной и полной мощностях. В цепях переменного тока в связи с периодическим изменением электрического тока энергия электрических и магнитных полей периодически изменяется и между этими полями и источником электрической энергии происходит обратимый периодический процесс обмена электрической энергией. Скорость такого обратимого процесса обмена электрической энергией между источником и электрической цепью характеризуется понятием реактивная мощность Q[ ВАр], (Вольт-Ампер реактивный). Одновременно в электрической цепи переменного тока происходит необратимый процесс преобразования электрической энергии в тепло, свет и другие виды энергии, т.е. в работу. Скорость такого необратимого процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт], (Ватт). Таким образом, в общем случае в цепи переменного тока одновременно происходят два процесса: процесс преобразования электрической энергии в другие виды (в работу) и процесс обратимого периодического обмена энергией между источником и цепью. Эти два одновременно протекающих процесса, накладываясь друг на друга, создают в цепи сложный единый энергетический процесс, для характеристики которого вводится понятие полная мощность S[ВА], (Вольт-Ампер). 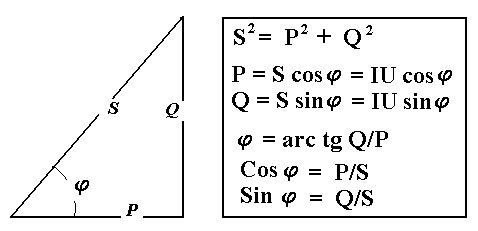Полученные энергетические соотношения могут быть условно представлены на плоскости в геометрической форме - в виде прямоугольного треугольника - треугольника мощностей, из которого могут быть получены дополнительные формулы, необходимые для выполнения электротехнических расчетов. 11. Последовательная цепь переменного тока, содержащая резистивный, индуктивный и емкостный элементы. Основные соотношения и особенности цепи. Электрическая цепь, содержащая индуктивный, активный и ёмкостный элементы, является одним из случаев соединения реактивных элементов (индуктивности и ёмкости), в котором обмен реактивной энергией возможен не только между источником электрической энергии и реактивным элементом цепи, но и между реактивными элементами внутри самой цепи. Такая цепь является последовательным колебательным контуром, в котором существует периодический обмен электрической энергией между переменным магнитным полем индуктивности и переменным электрическим полем ёмкости. При включении (L- R- C) - цепи в сеть переменного тока на напряжение uв ней протекает ток i = ImSinωt 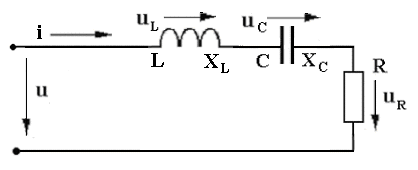 Для такой цепи по второму правилу Кирхгофа для мгновенных значений напряжений можно записать: u = uL + uC + uR, - или, переходя к действующим значениям напряжений, можно записать в векторной форме:  , U - напряжение на зажимах питающей сети (напряжение цепи), U L = I X L - напряжение на индуктивном элементе (индуктивное напряжение) опережает по фазе ток- U R = I R - напряжение на активном элементе (активное напряжение) совпадает по фазе с током , U С = I X С - напряжение на ёмкостном элементе (ёмкостное напряжение) отстает по фазе от тока В зависимости от соотношения величин реактивных сопротивлений различают три режима работы электрической цепи: 1. (X L > X C ) - цепь обладает активно-индуктивным характером. 2. (X L < X C ) - цепь обладает активно-ёмкостным характером. 3. (X L = X C ) - особый режим работы последовательной (L- R- C) цепи - резонанс напряжений - цепь обладает активным (резистивным) характером. 1. Активно-индуктивный режим работы последовательной (L- R- C) цепи возникает при условии X L > X C (U L > U C) и полученные при этом соотношения можно представить на плоскости в виде векторной диаграммы, на которой вектор общего напряжения U (напряжения на зажимах цепи) является замыкающей многоугольника векторов U L , U R и U C : 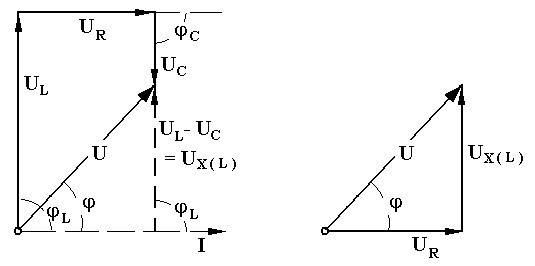 Вектор ( U L - U C ) = U Х ( L) - определяет результирующе напряжение на индуктивном и ёмкостном элементах, т.е. является реактивной составляющей напряжения цепи U (в данном случае - индуктивной составляющей напряжения цепи). Если вектор напряжения цепи U разложить на активную составляющую (U R - совпадающую по фазе с током) и реактивную составляющую (U X - ортогональную к току), получим прямоугольный треугольник напряжений последовательной цепи, образованный векторами U, U R = I R и U Х (L) = I X L - I X С = I (X L - X С ). Из полученного треугольника напряжений можно записать: U 2 = (I R)2 + [I (X L - X С )]2 или  -откуда получаем выражение закона Ома для последовательной (R- L- С) цепи переменного тока:  , здесь  - полное сопротивление (R- L- С) цепи.Разность реактивных сопротивлений (X L - X С ) = Х Э - называется эквивалентным реактивным сопротивлением, определяющим реактивный характер последовательной (R- L- С) цепи. В данном случае соотношение (X L - X С ) > 0 определяет индуктивный характер цепи, а разность (X L - X С ) = Х Э L - называется эквивалентным индуктивным сопротивлением (R- L- С) цепи. В этом случае последовательную (R- L- C) цепь на эквивалентной схеме замещения можно представить в виде последовательного соединения резистивного R и эквивалентного индуктивного Х Э L элементов: 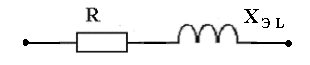 и записать закон Ома для действующих значений: Из треугольника напряжений можно получить скалярные прямоугольные треугольники - треугольник сопротивлений (если стороны треугольника напряжений разделить на силу тока I) и треугольник мощностей (если стороны треугольника напряжений умножить на силу тока I). Из этих треугольников можно получить дополнительные количественные соотношения, необходимые для расчета электрической цепи: 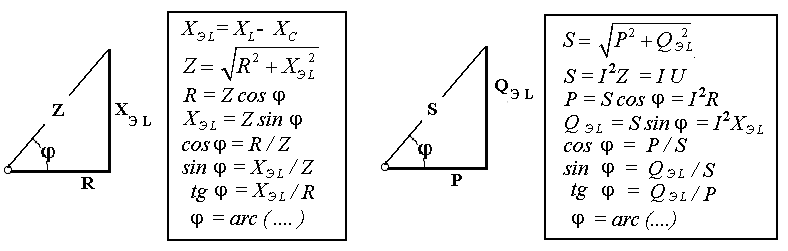 2. Активно-ёмкостный режим работы последовательной (L- R- C) цепи возникает при условии X L < X C (U L < U C) и полученные при этом соотношения можно представить на плоскости в виде векторной диаграммы, на которой вектор общего напряжения U (напряжения на зажимах цепи) является замыкающей многоугольника векторов U C , U R и U L : Вектор ( U L - U C ) = U Х ( C ) - определяет результирующе напряжение на индуктивном и ёмкостном элементах, т.е. является реактивной составляющей напряжения цепи U (в данном случае - ёмкостной составляющей напряжения цепи). Если вектор напряжения цепи U разложить на активную составляющую (U R - совпадающую по фазе с током) и реактивную составляющую (U X - ортогональную к току), получим прямоугольный треугольник напряжений последовательной цепи, образованный векторами U, U R = I R и U Х (С ) = I (X L - X С ). 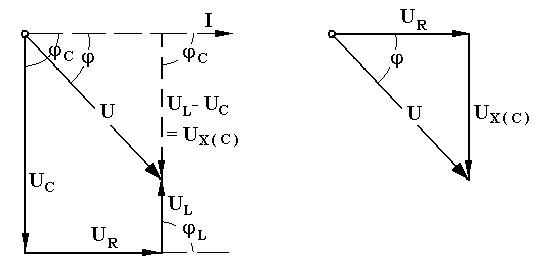 Разность реактивных сопротивлений (X L - X С ) = Х Э - называется эквивалентным реактивным сопротивлением, определяющим реактивный характер последовательной (R- L- С) цепи. В данном случае соотношение (X L - X С ) < 0 определяет ёмкостный характер цепи, а модуль разности [X L - X С ] = Х Э C - называется эквивалентным ёмкостным сопротивлением (R- L- С) цепи. В этом случае последовательную (R- L- C) цепь на эквивалентной схеме замещения можно представить в виде последовательного соединения резистивного R и эквивалентного ёмкостного Х Э С элементов: 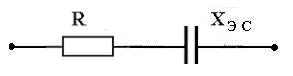 и записать закон Ома для действующих значений: .здесь - полное сопротивление (R- L- С) цепи.Из треугольника напряжений можно получить скалярные прямоугольные треугольники - треугольник сопротивлений (если стороны треугольника напряжений разделить на силу тока I) и треугольник мощностей (если стороны треугольника напряжений умножить на силу тока I). Из этих треугольников можно получить дополнительные количественные соотношения, необходимые для расчета электрической цепи: 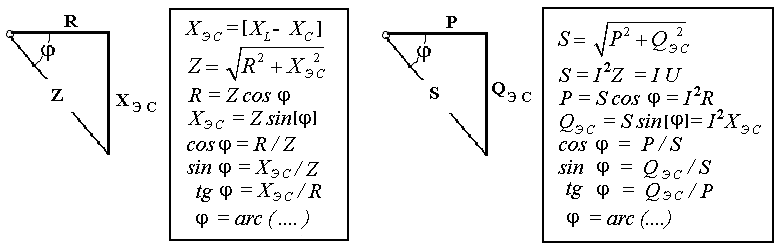 3. Особый режим работы - резонанс напряжений – возникает в последовательной (L- R- C) цепи при условии X L = X C (U L = U C). Полученные при этом соотношения можно представить на плоскости в виде векторной диаграммы, на которой вектор общего напряжения U (напряжения на зажимах цепи) является замыкающей многоугольника векторов U C , U R и U L : 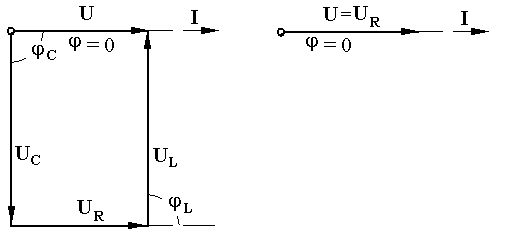 При резонансе напряжений разность реактивных сопротивлений (X L - X С ) = 0, т. е. в цепи отсутствует эквивалентное реактивное сопротивление Х Э = 0 и последовательную (R- L- C) - цепь на эквивалентной схеме замещения можно представить в виде только одного резистивного R элемента:  .В этом случае можно записать закон Ома для действующих значений:  Основные количественные соотношения в последовательной (R- L- C) - цепи при резонансе напряжений можно представить в следующем виде: 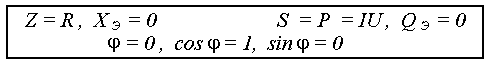 12. Расчет последовательной цепи переменного тока. Схема замещения. Резонанс напряжений. Особенности цепи. При расчете электрической цепи обычно известны приложенное напряжение и сопротивления элементов цепи, а в результате расчёта необходимо определить ток и построить векторную диаграмму электрической цепи. Неразветвлённая цепь переменного тока в общем случае является многоэлементной и может содержать различные комбинации последовательно включенных реальных и идеализированных элементов: 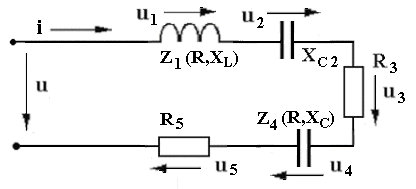 Такая последовательная цепь путем суммирования сопротивлений содержащихся в ней активных и реактивных элементов может быть приведена к простой эквивалентной схеме замещения, содержащей в общем случае три идеальных элемента: .  - здесь R = ∑ Ri = R 1 + R 3 + R 4 + R 5 - общее активное сопротивление последовательной цепи, Х L = ∑ XLi = X L 1 - общее индуктивное сопротивление, X C = ∑ XCi = X C 2 + X C 4 - общее ёмкостное сопротивление, X L - X C = X Э - эквивалентное реактивное сопротивление,  - полное сопротивление последовательной цепи., - сдвиг фаз в последовательной цепи.По закону Ома определяется ток в цепи:  ,после чего определяется напряжение на каждом из элементов цепи:  .По полученным результатам и известному сдвигу фаз в каждом из элементов  строится векторная диаграмма. Построение векторной диаграммы для последовательной цепи удобно начинать с тока I , общего для всех элементов (участков) цепи, вектор которого обычно откладывают по горизонтали. Из диаграммы следует, что ток в цепи I опережает общее напряжение на зажимах цепи U и общий (результирующий) сдвиг фаз в цепи φ < 0, т. е. в этом случае последовательная цепь по характеру является активно – ёмкостной ( R - С). Эквивалентную схему замещения такой цепи можно изобразить в виде последовательного соединения активного R и эквивалентного ёмкостного элементов X Э С = X L - X C = ∑ X L i- ∑ X C i = X L 1 – (X C 2 + X C 4 ). 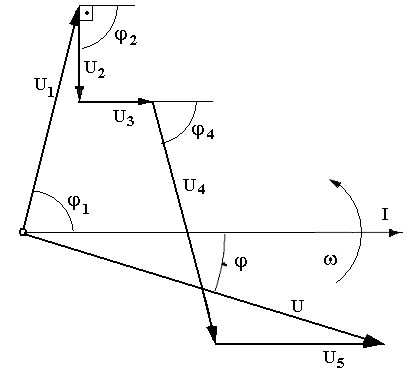 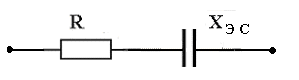 Явление резонанса напряжений Режим работы реальной электрической цепи переменного тока, содержащей реактивные элементы (индуктивности и ёмкости), при котором ток в цепи совпадает по фазе с напряжением, называется электрическим резонансом. В зависимости от структуры электрической цепи различают два вида электрического резонанса: - резонанс напряжений - возникает в последовательной цепи переменного тока, содержащей индуктивность и ёмкость, - резонанс токов - возникает в параллельной цепи переменного тока, содержащей ветви с индуктивностью и ёмкостью. Резонанс напряжений возникает в последовательной цепи переменного тока -последовательном колебательном контуре, содержащем индуктивность и ёмкость. Из условия X L = Х C можно найти собственную (резонансную) частоту контура f 0 , определяемую параметрами L [Гн] и C [Ф] контура, при которой в цепи возможен резонанс напряжений:  (формула Томсона).В цепях переменного тока явление электрического резонанса возникает, когда вынужденная частота источника электрической энергии (частота питающей сети) f совпадает с резонансной частотой контура f = f0 . В последовательной цепи, в общем случае содержащей несколько реактивных элементов, резонанс напряжений возникает при условии: ∑ X L= ∑ X C . В простейшем случае, когда цепь содержит по одному реактивному элементу это условие можно записать: X L = Х C ωL = 1/(ωC Из этого условия следует, что резонанс напряжений можно получить в цепи следующими способами: 1. Изменением собственной (резонансной) частоты цепи f 0 = var, для чего можно изменять: - индуктивность: L = (w2 μ S)/l, [Гн], при этом обычно изменяют магнитную проницаемость среды μ путем перемещения ферромагнитного (железного) сердечника и изменения длины его части, находящейся в катушке. - емкость : C = ε S/d. 2. Изменением частоты питающего тока f = var, так чтобы частота питающей сети стала равной резонансной частоте контура f = f 0 . Особенности цепи при резонансе напряжений: 1. Электрическая цепь обладает резистивным (активным) характером: ток совпадает с напряжением (ток и напряжение синфазны), сдвиг фаз в цепи φ = 0 , Z = R и схема замещения содержит только один резистивный элемент: 2. Коэффициент мощности сos φ = 1 – вся поступающая в цепь электрическая энергия преобразуется в работу, как полезную, так и различного рода потери. 3. Полное сопротивление цепи минимально:  и равно активному сопротивлению цепи: X L – X C = 0 Z = R = min . 4. Ток в цепи максимален: I = U / Z = U / R = max и при малой величине активного сопротивления может достигать очень больших и опасных для цепи значений.
6. Цепь не потребляет от сети реактивную мощность Q = I U sin φ = 0 -обмена реактивной энергией между источником электрической энергии и цепью не происходит. Однако в самой цепи существует реактивная мощность и между реактивными элементами (катушкой и конденсатором) происходит обмен реактивной энергией. При этом индуктивная и ёмкостная составляющие реактивной мощности в цепи могут быть очень большими, поскольку при резонансе напряжений происходит их взаимная компенсация. 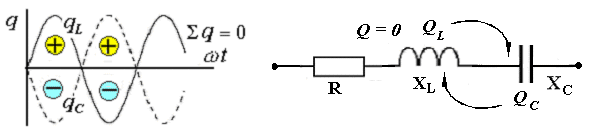 7. При резонансе напряжений (Х L = Х C) или при условиях близких к резонансу (Х L ≈ Х C) возможно возникновение явления перенапряжений на реактивных элементах, когда напряжение на катушке и конденсаторе может превысить приложенное к цепи напряжение. Явление перенапряжений возникает всегда при условии: Х L = Х C > R , а также может возникать при условии: Х L ≈ Х C > R . 13. Расчет параллельной цепи переменного тока. Последовательная эквивалентная схема замещения. Резонанс токов. Особенности цепи. При расчете разветвлённой электрической цепи обычно известны приложенное напряжение и сопротивления элементов цепи, а в результате расчёта необходимо определить токи в ветвях и в неразветвлённой части цепи, параметры эквивалентной последовательной схемы замещения и построить векторную диаграмму. Разветвлённая цепь переменного тока в общем случае может содержать несколько различных по характеру ветвей с различной комбинацией последовательно включенных реальных и идеализированных элементов. В отличие от расчета последовательной цепи в расчете параллельной цепи обычно используется метод проводимостей. Любой элемент (участок) электрической цепи характеризуется параметрами – комплексным сопротивлением  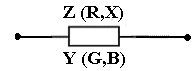[Ом] или обратной величиной – комплексной проводимостью Y [См]:   .Комплексная проводимость  , как и всякая комплексная величина, может быть представлена в алгебраическом виде:  , Здесь Y = [ ] = 1/ Z - модуль комплексной проводимости - полная проводимость,G - действительная составляющая комплексной проводимости - активная проводимость, B - мнимая составляющая комплексной проводимости - реактивная проводимость, - угол сдвига фаз в рассматриваемом элементе. 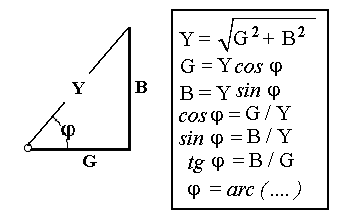 В зависимости от того, каким характером обладает рассматриваемый элемент (индуктивным или ёмкостным) различают два вида реактивной проводимости: B L - индуктивная проводимость, B С - ёмкостная проводимость.Для вычисления активной и реактивных проводимостей обычно пользуются формулами, которые легко получить через известные (заданные) сопротивления элемента цепи R, X L или X C и Z , выразив коэффициент мощности cos фи из треугольника сопротивлений ( cos = R / Z ): G = Y cos = (1/ Z ) cos = R / Z 2 [Ом], B L = Y sin = (1/ Z ) sin = X L / Z 2 [Ом], B C = Y sin = (1/ Z ) sin = X C / Z 2 [Ом]. Указанные соотношения могут быть представлены на плоскости в виде прямоугольного треугольника проводимостей: (*) Если какая либо k- ветвь содержит несколько активных и реактивных элементов, то она должна быть приведена к эквивалентной схеме по формулам последовательной цепи: R k = ∑ R k i , X k (L,C) = ∑ X k i (L) - ∑ X k i (C). 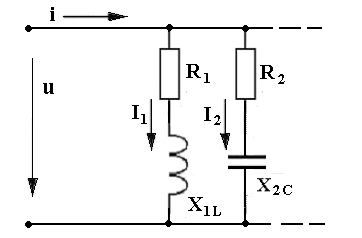 МЕТОДИКА РАСЧЕТА ПАРАЛЛЕЛЬНОЙ ЦЕПИ 1. Определяются комплексные сопротивления ветвей и токи в ветвях Первая ветвь. Из треугольника сопротивлений для первой ветви 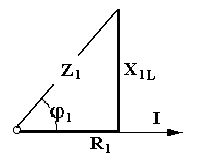 определяется полное сопротивление и сдвиг фаз в 1- ветви  и 1 = arc tg R 1 / X 1 L , после чего находят комплексное сопротивление и ток в 1- ветви:  ,  Вторая ветвь. Из треугольника сопротивлений для второй ветви 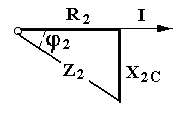 определяется полное сопротивление и сдвиг фаз в 2- ветви  и 2 = arc tg R 2 / X 2 C , после чего находят комплексное сопротивление и ток в 2- ветви:  ,  .2. Определяются комплексные проводимости и параметры треугольников проводимостей ветвей Первая ветвь. 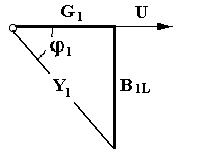  Вторая ветвь. 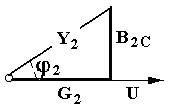  3. Определяется комплексная проводимость всей цепи Комплексная проводимость разветвлениянаходится как сумма комплексных проводимостей всех ветвей:  , .Здесь:  - действительная составляющая комплексной проводимости разветвления - активная проводимость всей цепи,  -мнимая составляющая комплексной проводимости разветвления - эквивалентная реактивная проводимость всей цепи, - полная проводимость всей цепи, = arctg В Э /G - угол сдвига фаз между током I в неразветвленной части цепи и напряжением на зажимах цепи U (общий сдвиг фаз в параллельной цепи). В зависимости от соотношения величин реактивных проводимостей ветвей (∑ B k C и ∑ B k L ) различают три режима работы параллельной цепи: 1. ∑ B k C< ∑ B k L - цепь обладает активно-индуктивным характером:∑ B k C- ∑ B k L = В Э L. 2. ∑ B k C > ∑ B k L - цепь обладает активно-ёмкостным характером: ∑ B k C- ∑ B k L = В Э С. 3. ∑ B k C = ∑ B k L В Э- особый режим работы параллельной цепи - резонанс токов - цепь обладает активным (резистивным) характером. 1. Активно-индуктивный режим работы параллельной цепи : ∑ B k C< ∑ B k L . 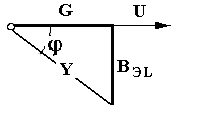 В этом случае комплексная проводимость цепи  и полученные при этом соотношения можно представить в виде треугольника проводимостей разветвления 2. Активно-ёмкостный режим работы параллельной цепи: ∑ B k C> ∑ B k L . В этом случае комплексная проводимость цепи 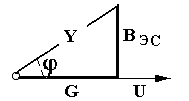 и полученные при этом соотношения можно представить в виде треугольника проводимостей разветвления: 3. Особый режим работы - резонанс токов – возникает в параллельной цепи при условии ∑ B k C = ∑ B k L В Э в этом случае комплексная проводимость цепи равна активной проводимости разветвления:  .IV. Определяются комплексное сопротивление разветвления и ток в неразветвленной части цепи  ,  .V. Определяются параметры эквивалентной последовательной схемы замещения параллельной цепи  , откуда получаем:  ,  ,  .Характер эквивалентного реактивного сопротивления схемы замещения ( Х Э ) определяется характером эквивалентной реактивной проводимости разветвления  , поэтому возможны три варианта последовательной схемы замещения параллельной цепи:  V1. Построение векторной диаграммы параллельной цепи По полученным значениям токов в ветвях ( I 1 и I 2) и сдвигам фаз (φ 1 и φ 2 ) строится векторная диаграмма разветвления (при построении векторной диаграммы примем, что все токи и углы сдвига фаз найдены такими, как они указаны на диаграмме). Построение векторной диаграммы для параллельной цепи удобно начинать с напряжения U, общего для всех ветвей, вектор которого обычно откладывают по горизонтали. 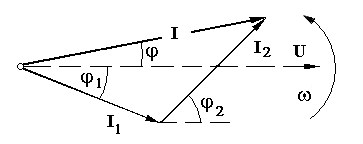 Из диаграммы следует, что общий ток в неразветвленной части ток цепи I опережает напряжение на зажимах цепи U и общий (результирующий) сдвиг фаз в цепи φ < 0, т. е. в этом случае параллельная цепь по характеру является активно – ёмкостной ( R - С).Эквивалентную схему замещения такой цепи можно изобразить в виде последовательного соединения активного 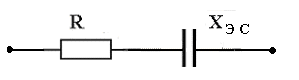 и ёмкостного элементов  ЯВЛЕНИЕ РЕЗОНАНСА ТОКОВРезонанс токов возникает в параллельной цепи переменного тока, содержащей ветви с индуктивностью и ёмкостью– в параллельном колебательном контуре, когда вынужденная частота источника электрической энергии (частота питающей сети) f совпадает с резонансной частотой контура f = f0 . В параллельной цепи, в общем случае содержащей несколько ветвей с реактивными элементами, резонанс токов возникает при условии: ∑ B k C = ∑ B k L В Э =0 В простейшем случае, когда цепь содержит две ветви - одну с индуктивностью L и вторую с ёмкостью С , как в рассмотренном выше примере, это условие можно записать: B L = B C , откуда находится резонансная частота параллельного колебательного контура:  Из условия электрического резонанса f = f0следует, что резонанс токов в параллельной цепи можно получить следующими способами:1. Изменением собственной (резонансной) частоты цепи f 0 = var, для чего можно изменять: - индуктивность: L = (w2 μ S)/l, [Гн], при этом обычно изменяют магнитную проницаемость среды μ путем перемещения ферромагнитного сердечника и изменения длины его части, находящейся в катушке. - емкость: C = ε S/d , сопротивление резистивных элементов: R (1, 2 ) = ρ0 [1+α (T1 – T0 )] l /S . 2. Изменением частоты питающего тока f = var, так чтобы частота питающей сети стала равной резонансной частоте контура f = f 0 . Особенности цепи при резонансетоков: 1. Электрическая цепь обладает резистивным (активным) характером: ток совпадает с напряжением (ток и напряжение синфазны), сдвиг фаз в цепи φ = 0 , Z = R и схема замещения содержит только один резистивный элемент: 2. сos φ = 1 – вся поступающая в цепь электрическая энергия преобразуется в работу, как полезную, так и различного рода потери.3. Полная проводимость параллельной цепи минимальна и равна активной проводимости цепи: В Э = 0 Y = G = min . 4. Общий ток в неразветвленной части цепи минимален: I = U Y = U G = min, однако токи в ветвях в зависимости от величины реактивных проводимостей могут достигать очень больших значений. 5. Цепь потребляет от сети только активную мощность, равную полной мощности: P = I U сos φ = G U2 = S . 6. Цепь не потребляет от сети реактивную мощность Q = I U sin φ = 0 -обмена реактивной энергией между источником электрической энергии и цепью не происходит. Однако в самой цепи существует реактивная мощность и между ветвями с реактивными элементами (катушкой и конденсатором) происходит обмен реактивной энергией. 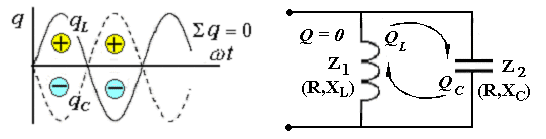 14. Преимущества трехфазных систем. Трех- и четырехпроводные системы. Основные определения. Соединение фаз потребителя по схеме «Звезда» и «Треугольник» (схемы и основные соотношения). В современных системах передачи электрической энергии на дальние расстояния, электроснабжения и распределения электрической энергии применяются трехфазные цепи, которые по сравнению с однофазными имеют значительные преимущества:
Трёхфазная цепь – представляет собой совокупность трёх однофазных цепей, соединённых в общую электрическую цепь и содержащую: источник трёхфазной системы ЭДС (трёхфазный генератор); трёхфазный потребитель или приемник электрической энергии (нагрузка); соединительные провода (линия электропередачи). |