все лекции по тд и тп. Закон тд для закр неподвиж сисмы. Сисма не обменивающаяся с окр средой вещвом называется закрытой
 Скачать 1.36 Mb.
|
|
1 закон ТД для закр. неподвиж. сис-мы. Сис-ма не обменивающаяся с окр. средой вещ-вом называется закрытой. Предполагаем что преобр-е эн-и происх. только в форме теплоты и мех. работы. Измен-е потенц. эн-и связанной с положением сис-мы в проср-ве пренебрегаем, рабочее тело сис-мы считаем неподвижным. Согласно уравнению E=Eк+ Eп + U : dEк=0 dEп=0 dE=dU Полную энергию можно изменить за счет подвода в сис-му теплоты (dQ) и работы (dL) (dE=dQ-dL) Поэтому dQ=dE+dL=dU+dL (1) dq=du+dl (2) l=L/m-удельная работа сис-мы Согласно (1) и (2) 1 закон ТД гласит: Подводимая из вне теплота затрачивается на изменение внутренней эн-и сис-мы и на совершениесис-мойработыпротиввнеш. сил. Без потерь в закр. неподвиж. сис-му может быть подведена или отведена только работа измен-я объема сис-мы. (2): dq=du +pdυ (3) Другой вид этого закона получим из (3): dq=du+d(pυ)-υdp=d(u+pυ)-υdp Или dq=di-υdp (4) В интегральной форме (3) и (4) при Cv=const Cp=const: 2 q=Cv(T2-T1) + ∫pdυ 1 2 q=Cp(T2-T1) - ∫υdp 1ый з-н термодинамики для закрытой подвижной системы Е= Е+Е+ U Для подвиж. системы в развернутой форме запас полной энергии примет вид.  z- высотатогда 1ий з-н термодинамика представим. Или в интегральной форме Работа сил изменяющая как внут сост сист (например работа изменяющих обьем)так и внш её состояние(работа сил перемещающих систем в целом) I з-н ТД для открытой системы(стационарного поточного процесса. 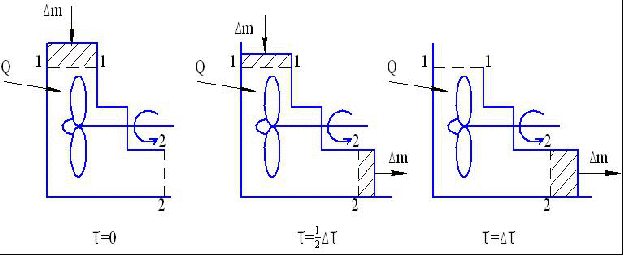Рассм.откр.систему м/у сеч-ми 1-1, 2-2. В систему подводится теплота Q и тех.работа Lтех (работа вала).Наблюдение проведем за отрезок времени Δτ. За это время в откр. Систему(контрольное пространство) поступает масса в-ва Δm ч/з сеч-е 2-2. Добавим к откр.системе с массой m0 м/у сеч-ми 1-1, 2-2 массу Δm. В рез-те получим систему с массой m0+ Δm. Вел-ну Δm будем полагать малой.Применим I з-н ТД к закрытой подвижной системе: Q= ΔE+L (1.25), где L= Lтех+ΔL – общая работа , состоящая из тех.работы и работы, затраченной на проталкивание массы Δm ч/з открытую систему. ΔL найдем по формуле ΔL=P2ΔV2- P1ΔV1= Δm(p2 v2- p1 v1), (1.26), где v1=V2/ Δm – удельный объем, характеризующий уменьшение объема условно закрытой системы вследствие поступления массы Δm. v1=V2/ Δm – уд.объем, характеризующий увеличение объема условно закрытой системы из-за выхода массы Δm. Изменение запаса энергии равно: ΔE=E2-E1=(E0+ Δm(u2+w22/2+gz2))-( E0+ +Δm(u1+w12/2+gz1)),(1.27), где E0 –запас полной энергии открытой системы (м/у сеч-м 1-1, 2-2). Подставляя 1.26 и 1.27 в 1.25 получим: Q= Δm(u2+w22/2+gz2)- Δm(u1+w12/2+gz1)+ Δm(p2 v2- p1 v1)+ Lтех или Q= Δm(i2+w22/2+gz2)- Δm(i1+w12/2+gz1)+ Lтех (1.28). Для удельных величин: q- lтех=i2-i1+1/2·(w22-w12)+g(z2-z1) (1.29) q- lтех=i2*-i1*+ g(z2-z1) (1.30), где i*=(i+ w2/2) – Кинетическая энергия. Подведенная теплота и тех.работа приводят к изменению полной энтальпии и потенциальной энергии в-ва, проходящего ч/з открытую систему.  Компрессор.2ой З-н термодинамики: На основание опытов установлена что все реальные процессы могут самопроизвольно протикать только в одном направление например теплота переходит от теплого тела к холодному газ вытекает только из сосуда с высоким давлением вокруг пространства к непод-му газу в сосуде можно только подвести работу вала.2-щй З-н основан на опыте и может быть сформулирован в виде принципа не обратимости .Все естественные и реальные проц-ы не обратные . Это означает что в природе нет проц-в которые можно былабы в отношение всех их результатов полностью обратить . Т.е вернуть в начальное состояние без остаточных измерений в окружающей среде . Принцип не обратимости в термод-ке часто заменяется на частные формолеровки как например Планк предложил 2-ой закон формоли-ки . Все процессы соправаждающейся трением не обратимы . Клаудиус утверждал что не возможно передать теплоту от более холодного тела к более теплому . Если одновременно не произвести свазанные с этих другое измерение . Щчень часто при расмотренние 2-го З-на термо используется постулаты основные на частных соображениях а работе тепловых двигателей . Согласно Томсану не возможен процесс единственный результат кот-го состоял в поглащение теплоты от нагревателя и полном преобразование этой теплоту в работу . Планк утверждал что не возможно построить периодически действительную машину единственным результатом действие которое былабы совершение механической работы за счет оплатнение теплового резервуара . Для получение полезной работы или для переноса теплоты от холодного источника к горячему необхадимо компенсирование процесса . Круговые проц или Циклы : Процесс возвращается в систему в начальное состаяние наз-ся круговым процессом . Цикл состаящий из обратных процессов наз-ся обратным . Если цикл протекает по движению часовой стрелки -1-2-3-4-1 то его наз прямым . В противоположном случае 1-4-3-2-1 наз обратным . В цикле с стационарным циркулированием рабочим телом поток вещества протекает через последовательно включенные открытые системы для этих систем справедлив 1 –ый З-н термо. q12-l12 = i*2-i*1 +g(z2-z1) q23-l23 = i*3-i*2 +g(z3-z2) q34-l34 = i*4-i*3 +g(z4-z3) q41-l41 = i*1-i*4 +g(z1-z4) Сложим их получим :q12+q32+q34+q41=l12+l23+l34+l41 Следовательно суммарная полезная работа цикла = энергии подводной к рабочему тело в форме теплоты полученной как разность отведенных теплот другим словом можно сказать – В циклах энергии подводимая к рабочему телу в форме теплоты частична прев полезную работу и частица отводится в форме теплоты . в формуле пркдпологалось что что сумма qij >0 . те в частных процессах теплоты подведено > чем отведено такие циклы соответ-но тепловым машин если сумма qij <0 то сумма lij <0 . След-но суммарная полезная работа будет подводится в цикле . Такие цикли соответствуют тепловым насосам и холодным установкам . В тепловых Маш рабочие тело осущ-т всегда прямой кругавой процесс . А в тепловых насосах обратный . Эффек-ть цикла тепловой Маш можно определить с помощью термо КПД Mt=lц/q = q1-q2/q1 = 1-q2/q1 Где l ц = сумма lij =работа цикла Q1 q2 – удельные подведенная и отвед теплота (q1-q2= сумма qij) Критические параметры газового потока. Параметры потока, когда скорость газа равна местной скорости звука, называется критическим. При Т=Ткр Wкр=акр  , где Т*- температура торможения Wкр=акр= . При Ткр величина ркр равна Для воздуха к=1,4 . При lтех=0 найдем . после логарифмирования и дифференцируя уравнение расхода lnρ+lnW+lnF=ln const . Подставив вместо его значение получим (1)Из уравнения (1) видно, что при М<1, то есть при докритическом перепаде давление  и сужение канала скорость увеличивается. А при сверхзвуке наоборот.Максимальная скорость будет в самом узком сечении, т е на срезе конического сопла. При критическом перепаде, т е при 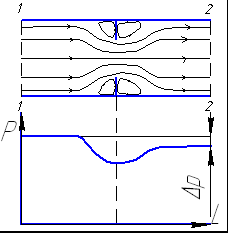скорость в этом сечении равно скорости звука (М=1). Если перепад давления сверхкритический, то на срезе скорость равна скорости звука, но статическое давление возрастет и станет больше, чем давление в окружающей среде. . При р* =const статическое давление на срезе при М=1 достигнет минимально возможной величины. В этом случае расход газа достигнет максимальной величины. Дальнейшее снижение давления в окружающей среде не вызовет дальнейшего увеличения расхода газа. При в пределах сопла происходит расширение газа и расположенная энергия газа полностью расходуется на повышение кинетической энергии.При сверхкритическом перепаде в пределах сопла поток расширяется не полностью, а только до критического давления. Дальнейшее расширение газа до давления р происходит за пределами сопла. |