все лекции по тд и тп. Закон тд для закр неподвиж сисмы. Сисма не обменивающаяся с окр средой вещвом называется закрытой

• Название: Закон тд для закр неподвиж сисмы. Сисма не обменивающаяся с окр средой вещвом называется закрытой
• Анкор: все лекции по тд и тп.doc
• Дата: 29.12.2017
• Размер: 1.36 Mb.
• Имя файла: все лекции по тд и тп.doc
• Тип: Закон; #13436
• Категория: Физика
• страница: 3 из 6

Необратимые термодинамические процессы

Если процесс необратим то энтропия рабочего тела увеличивается за счет внутреннего производства энтропии.

Согласно 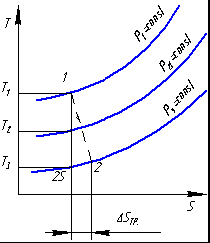; т.к. след-но конечные состаяния в обратимом и необратимом процессе будут различны из-за различных конечных значений энтропии



Рассмотрим обратимый процесс 1-2s и необратимый 1-2 адиабатного расширения рабочего тела до одного и того же давления. Необратимость обусловлена трением , для



видно что из-за перехода части работы в теплоту трения .
Для вычисления заменим процесс 1-2 на два обртимых проц-а и . Проц. - изоэнтропный, а - изотермический. В изоинтропном =0, а в изотермическом . Рассмотрим необратимый процесс расширения газа в вакуоме


Сосуд теплоизолирован (адиабатная система) после расширения газа ; dq=0 и ; du=0 или след-но процесс расширения является изотермическим. Для изотермического проц-а увеличение энтропии в системе равно

т.е. из-за необратимости процессов внутри системы произойдет производство энтропии.

ОБРАТИМЫЕ И НЕОБРАТ ПРОЦЕССЫ

В термодинамике сист хар-ся с помощью физ-х вел или переменны. Если переменные принимают устойчивые значения, то сист нах-ся в определенном сост. Поэтому переменные системы наз её параметрами состояния. Термодинамическое сост сист опысивают внут параметрами сост. Сист нах-ся в равновесном сост если при изоляции её от воздействия внешной сферы среды параметры сост сист не изменяются. Поэтому равновесное сост сист может изменится только вследствие внш воздействмя. Процесс при котором изм-ся сост сист наз-ся термодинамическим процессом. Карно вел понятие идеализированный процесс.таким процессом яв-ся обратным процессом . Если система в которои протекает про_сс вернуть в начальное стояние так что во внешней среде не произойдет каких-либо изменений то процесс называется обратным . В пративном случае он называется необратимым . Обратный процесс сост из последовательности равновесных состояний . М/у которыми отсутствует диссипативный эффект . В реальности квази статические изменения состоят и при отсутствие диссипативный эффект не наблюдается но обратный процессы очень важны в термодинамике т.к харак-ся потери мех-ой энергии . Поэтому их можно использовтаь в качестве эталона при оценке эффективности в реальных процессов мех-х устройств.
Реальныегазы Все реальные газы явл. Парами соответствующих жидкостей.изобразим в pv различные состояния газа:точка К критическая точка,кот. Соответств. Критич параметры:Pкр.Tкр.Vкр.При критич состоянии исчезают различия между жидк и паром.I-газообразное состояние,II-некипящ жидкость,III-двухфазное состояние(кип жидк+сух пар).При t>tкр газ ни при каком давлении не может сконденсироваться.Для расчета параметров реальн газа часто используют уравн Вандер-Ваальса

где a/V^2

поправка на внутр давление,обусловл внутр притяжением молекул.b-поправка на обьем самих молекул.

Это уравнение качественно правильно описывает непрерыв переход из жидк состояния в газообразное.Уточнение расчетов пытались обеспечить,за счет зависимостей:и.В настоящее время тоеритич обосновано уравнение состояния в виде

Где z фактор сжимаемости.- вириальные коэф.,учитывающие взаимодействия соотв 2.3…молекул.Вириальные коэф. Определяются на основе знания зависимости взаимодействия молекул от расстояния между ними.

ПОлитропные процессы ид.газа

Используя ур:опред. Теплоемкость газа в политропном процессе:получаем (1)

Дифференцируя pV=Rt определяем величину (2)

Исключая dT из (1) с помощью (2) получим:

Пусть: (3).С учетом (3)ду примет вид:

Полагая n=const, в ходе термодинамического процесса проинтегр это уравнение, в результате получим, уравнение политроп процесса:nlnV+lnp=ln(const); или (4), где n показатель политропы.Заменив значения P и V в(4) с помощью pV=RT получим: или;

или .

Удельная работа расширения:;

. Это соотношение можно представить:.

Располагая работу в ,определяем;;.

Из (3)можно найти теплоемкость политропного процесса: (5),где и .Общее количество теплоты подведенное к газу равно.С помощью (5) найдем долю теплоты,расход на изменение внутр энергии работы тела:. Тогда доля теплоты идущ на совершение работы изменения обьема,равна:;

Изменение энтропии:;интегрирование этого уравнения дает:
Термич.поле. Градиент температуры.

Теория теплообмена- учение о самопр.необратимых процессах распр-я теплоты в пространстве. Для кол-й оценки теплоты, передаваемой в ед.времени ч/з произв.поверхность вводят понятие теплового потока Q [Дж/с=Вт].Тепловой поток, отнес-й к площади пов-ти наз-ся плотностью теплового потока или уд.теплов.потоком q [Дж/(с‡м²)=Вт/м²].

Под температурнымполемпонимают совокупность мгновенных значений температур во всех точках изучаемого пространства. Температура различных точек тела t определяется координатами х, у, zи временем т. Поэтому в общем случае t(r_в,τ)=t(x,y,z, τ),где r_в – радиус-вектор точки, x,y,z – координаты, τ– время. Поле, изменяющееся во времени наз-ся нестационарным или неустановившимся, в противном случае стационарным или установившимся, т.е. t(r_в)=t(x,y,z).В скалярном поле можно выделить поверхность в 3-х мерном случае и изолинии в двумерном случае, как пов-ти или линии с одинаковыми знач-ми т-ры (изотермич.пов-ти или изотермы).По расположению этих изолиний оценивают интенсивность изменения т-ры в различ.направлениях. Наиболее быстрое изменение скал.поля хар-ся градиентом:

где - оператор Набла.
Механизмы и законы переноса теплоты. Явление теплопроводности, теплоотдачи и излучения.

Различают 3 механизма (процесса) переноса теплоты: 1) теплопроводность (кондукция) – перенос распр-я энергии только вследствие взаимодействия структурн.частиц в-ва (молекул, ионов, атомов, своб.эл-нов).В чистом виде теплопр-ть имеет место в тв.телах, в неподвиж. слоях жидкости или газа.

2) Конвекция – прц.переноса теплоты вследствие перемещения относ-но больших масс в-ва в неоднородном поле тем-р. Этот процесс имеет место в движ.квазисплошных средах (жидкостях, газах, сыпучих средах, в плазме)

3) Излучение (радиация) – пр.переноса энергии, выделившейся вследствие тепл.движения в в-ве в виде э/м волн ч/з полносью или частично прозрачную для них среду.

Сложным теплообменом наз-ся пр-сы переноса теплоты одновр.неск. способами. Теплопередачей наз-ся пр-с теплообмена м/у средами, разделенными отчетливой границей (н-р, тв.тела - текучая среда, пов-ть раздела газ – жидкость или 2-х несмешивающихся жидкостей).

Теплопередача – процесс теплообмена м/у средами,разделенными некот.перегородкой. При расчете теплопроводности в среде пользуются з-ном Фурье: λ – коэф-т теплопроводности среды, Вт/(м‡гр). Для расчета теплопроводности применяют ф-лу или з-н Ньютона-Рихмана: Вт или Вт/м² (1.2), где α – коэф-т теплоотдачи [Вт/(м‡К]; t_f, t_w – Темп-ра теплоносителя и поверхности.

При α=const, t_f =const, t_w = const: .

Теплопередачу часто рассчитывают по формуле: , где k [Вт/(м²‡К)] – коэф-т теплопередачи; - температуры.

Тепловая хар-ка обратимых циклов.






Сравним(1,38) с(1,33) получим для ц.Карно:


Отношение q/T наз-ся приведённой теплотой, след-но в обратимом цикле Карно, алгебр-я сумма
приведённых теплот =0 (1,40) В (1,40) под q пон-ся алгебраическая величина q больше 0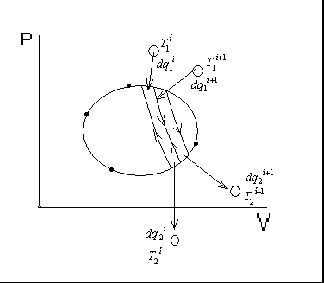
приводимой теплоты q меньше 0 отводимой теплоты. Выражение (1,40) называется тепловой характеристикой ц.Карно.Рассмотрим произвольный обратимый цикл.А-В-С-Д-А Он должен совершаться под воздействием бесконечно большого кол-ва в высших и низших ист-ов теплоты соот-но на линиях А-В-С и сжатия С-Д-А. Разобьем этот цикл на бесчисленное множество обратимых циклов Карно.Проведя адиабаты на бесконечно малом расстоянии друг от друга. Для каждого элементарного ц.Карно по аналогии с (1,40) можно записать что сумма приведённых теплот=0





или



Сложив подобные выражения получим:


Или


(1,41) Выражение (1,41) наз-ся уравнением или интегралом Клаузиуса

ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ

1. 
   ОСНОВНЫЕ ПОНЯТИЯ ТИ
   

Все тела при любых t излучают и поглощают энергию излучая, по кол-во этой энергии становится существенным только при высоких t или в условиях, когда перенос теплоты другими способами затруднен (при свободной конвенции особенно в разряженном газе)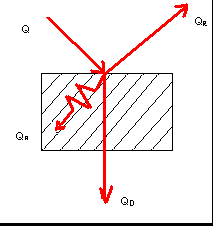

Поток излучения Q поглощ. телом не полностью .Часть энергии отражается, часть проходит сквозь тело, поэтому



A+R+D=1

- поглощ. способность

- отрож. способность

- пропуск. способность

Тело способное погл. всю падающую энергию, наз-ся абсолютно черным телом (А=1; R=D=0)

Тело отражающее всю падающую энергию наз-ся абс. Белым телом (R=1;A=D=0)

Если отражение имеет правильный характер тело наз-ся зеркальным (угол падения = углу отражения)

Большинство тв. и жид. тел не пропускают энергию излучения – не прозрачные тела. Поглощение энергии изл. в них происходит в тонком поверхностном слое. Для Ме=1мк.м , для неметаллов = 1мм (A+R=1). Тела пропуск. всю энергию падающ. Излуч. Наз-ся пропускающей способностью облад. газы.

Для монохроматического:

Излуч. Непрозрел. тел оценивается повыш. плотностью потока излучения Е ,

Е учитыв. излучение во всех напров-ях и при всех длинах воли () . В диапазоне от до во всех напровлениях излучается энергия .

хар-ет энергию ЭМ воли – наз-ся спектральной плотностью излучения

.