все лекции по тд и тп. Закон тд для закр неподвиж сисмы. Сисма не обменивающаяся с окр средой вещвом называется закрытой

• Название: Закон тд для закр неподвиж сисмы. Сисма не обменивающаяся с окр средой вещвом называется закрытой
• Анкор: все лекции по тд и тп.doc
• Дата: 29.12.2017
• Размер: 1.36 Mb.
• Имя файла: все лекции по тд и тп.doc
• Тип: Закон; #13436
• Категория: Физика
• страница: 4 из 6

ЗАКОНЫ ТЕПЛООБМЕНА ИЗЛУЧЕНИЯ.

Закон планка

Этот закон устан. зависим. Спектрального плотного потока излучение абсолютн. черного тела . 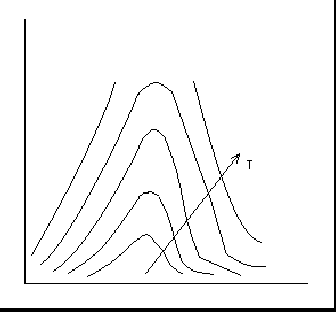длины волны и температуры Т.






Абс черное тело имеет сплошной спектр излучения , т.е излучает при всех длинах волн. Реальные тела могут иметь сплошной ,(диэл),или линейчатые спектры ( газы, пары) На рис сопоставлены зависимости

; для абсолютно черного и реального тел со сплошным или линейчатым спектрами.
Способность тела излучать энергию, характеризует спектральная степень черноты тела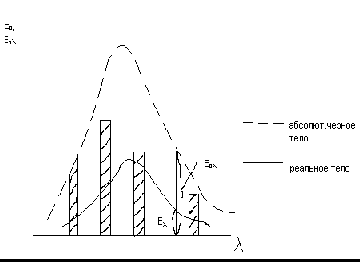

(1)

А также степень черноты тела

(2)

Т.е отношение изл способности реального тела к изл способности абс. черного тела.

Если величина имеет одинаковое значение для всех длин волн и температур то тело наз. Серым

Величина (3)

Из (1) с учетом (2) и (3) определили при (для серого тела)

или (4)

Для реальных тел неодинаково при разл. длинах волн, поэтому (4) для реальных тел не выполняется.

Теплообмен конвекцией.

1.Физ. условия теплообмена конвекцией.

Параметры потока описываются математической моделью, включающей уравнения неразрывности, Навье-Стокса и энергии. Особенностью процесса конвективного теплообмена является то, что среда, в которой происходят процессы распределения движутся. В результате движения вместе с массой жидкости или газа переносится и теплота. Поэтому процесс переноса теплоты определяется свойствами потока и его структурой – распределением скорости и режимом течения. При обтекании твердой поверхности на ней из-за прилипания реальной вязкой жидкости или газа образуются пограничный слой. Т. к. в пограничном слое имеется преобладающее направления вдоль твердой поверхности, то изменение параметров жидкости вдоль него гораздо меньше, чем вдоль направления перпендикулярного к нему. С учетом этого свойства Прандтли были получены уравнения пограничного слоя на основе упрощения уравнений Навье-Стокса. В плоском случае уравнения Прандтли для стационарного ламинарного пограничного слоя имеет вид:

(2.1)

(2,2)

Где U, V – компоненты вектора скорости

- плотность жидкости

P – давление жидкости

- проекции плотности массовой силы

- кинематическая вязкость.
Конвекция жидкости описывается левой частью уравнения (2,2), а диффузия (молекулярное перемешивание) последним членом этого уравнения. Уравнение энергии для ламинарного пограничного слоя имеет вид:

(2,3)

- коэффициент температуропроводности среды.

Т – температура в К.

Здесь также левая часть описывает конвективный перенос теплоты (за счет течения). Диффузионный перенос теплоты (за счет молекулярного перемешивания) характеризуется первым членом правой части. Очень часто последним диссипативным членом правой части из-за его малости пренебрегают. Жидкости и газы имеют небольшую теплопроводность , поэтому коэффициент амал, не велик и поперечный перенос теплоты. Поэтому ламинарный перенос теплоты создает большое термическое сопротивление потоку теплоты. В турбулентном пограничном слое из-за переноса турбулентных молей коэффициенты вязкости и теплопроводности увеличиваются на несколько порядков по сравнению с ламинарным течением. Коэффициенты вязкости, теплопроводности и температуропроводности тогда примут вид:



В результате интенсифицируется процесс переноса теплоты в поперечном направлении ТПС. Структура ТПС (турбулентный пограничный слой) становится сложнее у твердой поверхности, образуется ламинарный подслой, а над ним развитое турбулентное течение, в котором осуществляется конвективный и диффузионный перенос теплоты. Толщина ламинарного и турбулентного слоя соответственно равны:
, (2,5)

Где - число Рейнольдса.

- ускорение, скорость на пограничном слое. Видно, что толщина и структура пограничного слоя зависит от числа Рейнольдса. С увеличением динамической вязкости, уменьшается и увеличивается толщина пограничного слоя.

.

Поэтому в вязких жидкостях теплоотдача протекает менее интенсивно.
2,Факторы, определяющие интенсивность конвективного теплообмена.

На движение жидкости и ее теплообмен существенное влияние оказывают силы давления и массовые силы, а также форма обтекания поверхности. Определенное влияние также оказывают внешние турбулентности. Температуры потока и стенки входят в формулу Ньютона в явном виде:

.

Несмотря на это и влияют и на коэффициент теплоотдачи , т. к. от них зависят физ. свойства теплоносителя и диапазон их изменения. Коэффициент теплоотдачи в общем случае зависит от скорости потока, теплопроводности, вязкости, плотности, объемного расширения, удельной теплоёмкости, массовых сил (ускорения), формы и размеров тела, нестационарности, внешней турбулентности, неизотермичности и ряда других факторов. Большое число факторов затрудняют получение расчётных соотношений для его определения. Задача конвективного теплообмена аналитически решена только для простейших случаев обтекания стенки. Гораздо более сложные случаи обтекания тел рассчитываются путем численного интегрирования системы диф. уравнений (например, типа уравнений Прандтли или Навье-Стокса в общем случае). В многих случаях физический эксперимент остается единственным способом получения закономерностей, определяющих теплоотдачу.
Теплоотдача пластины с ламинарным и турбулентным пограничным слоем
На основе теории ламинарного пограничного слоя получена формула для определения коэффициента трения

,где (2,20)

Подставим это значение в (2,19), приняв ;

(2,21)

Определим средний коэффициент теплоотдачи на участке пластины для l:

(2,22) ,где ;

Безразмерный средний коэффициент теплоотдачи:

(2,23)

При определении коэффициента трения в турбулентном пограничном слое, можно воспользоваться формулой:

(2,24)

; f – инд-с, относиться к жидкости вне пограничного слоя.Полагая в (2,19) , и вводя в нее поправку , заменим на значение

(для ); Средние значения коэффициента теплопроводности:

(2,26);

Безразмерный средний коэффициент теплоотдачи:

(2,27)
теплоотдача при течении жидкости в трубах и каналах


l_н
l_н – длина участка гидродинамич-й стабилизации. гидродин нач участок – это участок до сечения, в котором смыкаются дин-ие погранслои. тепл нач участок – это участок до сечения, в котором смыкаются тепл погран слои. в трубах при Re=Wcp*d/V<(2…2,3)*10³ наблюд ламин-е течение. при сильной неизотерм-ти ламин теч-е может наруш-я гравит-й конвекцией. поэтому среди неизотерм ламин потоков различ вязкостный и вязкостногравитационный режимы течения. при числах Re=Gr*Pr=, где , ,течение будет вязкостным, иначе – вязк-гравитац-ым.

при Reпоток станов-я турб-ым, но в начале трубы сохр-ся участок с ламин погранслоем. при Re ТПС нач-ет формир-ся практич с начала трубы. при Reнаблюд переходный режим течения и теплообмена.

Для капельных жидкостей(Pr>1)

Теплоптоводность_ч/з_многослойную_цил-ую_стенку.'>Теплоптоводность ч/з многослойную цил-ую стенку.

t λ₁ λ_{2…………} λ_n

t_w1 t¹_w2

t¹_w3

t¹¹_w2

t¹¹_w3
t¹¹_w4 t_wn+1
r₁

r

r₂
r_n+1


Получим ф-лу для опред-ия теплового потока ч/з многослойную цил-ую стенку сост-ую из n слоёв с учётом контактного термич-го сопротивления м/у слоями. На границах стенки заданы ГУ 1-го рода.

при r=r₁ , t=t_w1

при r=r_n+1 , t=t_wn+1

Величины q_e (нижний коэф-ент не понятен,то-ли l то-ли e!!!) для i-го слоя и i-ой пов-ти контакта равны:





Записав эти потоки для каждого из n слоёв и n-1-ой пов-ти контакта и исключив после этого промеж-ые t-ры получим:

(1)

t-ры пов-ти стенки определим также как и в случае плоской стенки на ПР:

t¹_w3 из (1) t¹_w3=tw1-

Теплоптоводность ч/з цил-ую стенку.



На границах стенки заданы ГУ 1-го рода.

при r=r₁ , t=t_w1 при r=r₂ , t=t_w2

в этом случае тепловой поток имеет радиальное направление, темпер. поле одномерно. для стационар. одномер. задачи о теплопро-ти цил. стенки дифур-ие (1.5) в цил-й системе коорд-т при λ=const примет

(1.14)

введя новую переменную г=, преобр-ем (1.14)



после раздел-я перем-х и интегр-я получим lnu + lnr = lnC₁ (1.15)

потенцируя получим u*r= C₁

перейдя к первонач переем-м, запишем r= C₁ , а затем разделив получаем

t= C₁lnr+ C₂ (1.16)

искривление линии темпер-го поля в цил-ой стенке обуслов-о изменением плотности тепл-го потока q= при изменении радиуса цилиндра. при увеличении r величина площади F=2πrl, где l – длина стенки, также увел-ся. поэтому на больших r темп-ая линия проходит более полого и наоборот. Это правило сохр-ся и при обратном направ-ии тепл. потока(пунктир на рис.).

Подставив ГУ в (1.16) найдем C₁ и C₂ :

C₁= C₂ = (1.18)

преобр-м 1.16 с учетом 1.18 : (1.19)

где d₁ и d₂ – внутр и наруж диам-ы цилиндра, d – текущ-й диам-р цил-ра.

из (1.19) опред-им темпер-й градиент: = (1.20)

использ (1.20) найдем тепл-й поток ч/з стенку: Q=qF=-λ2πrl= (1.21)

тепловой поток на единицу длины (1.22)

величину назыв внутр термич сопр-ем цил стенки.обозначим плотности тепл. потока на внутр и внеш поверх-ях ч/з и . т.к. Q=l=πl=πl
=π=π (1.23)



Истечение и дросселирование газов.

Общее уравнение истечения газов.

При скорости w₂ в выходном сечении канала частица жидкости или газа перемещаться за время dτ на расстояние dx=w₂dτ в результате ч/з сечение -2- за время dτ пройдет масса dm=ρ₂F₂dx в единицу времени масса будет равна.

G=ρ₂w₂F₂ при стационарном течении расход газа ч/з любое сечение канала будет один и тот же в этом случае уравнение расхода или уравнении неразрывности будет иметь вид первого закона термодинамики для стационарного потока был получен ранее пренебрегая для газа изменением потенциальной энергии g(z₂-z₁) запишем этот закон в следующем виде

(3.2)
где

T^* - температура торможения

В дифференциальном виде уравнения (3.2) примут вид

(3.3)

Сопоставив (3.3) с ф-ой () получим уравнение энергии в другом виде

(3.4)

В конечном виде уравнение энергии запишется следующим образом



В качестве 3-го уравнения при расчете истечения газа используют уравнения состояния

pV=RTилиp=ρRT (3.6)

Истечение идеального газа.

q=0 иl_тех=0 в произвольном канале из (3.2) найдем

_(3.7)

где w₂=w – конечное значение скорости.

Это уравнение справедливо для идеального и реального газов для идеального газа используются pV=RTилиp=ρRT (3.6) и pV^k=const, TV^k-1=const, T^k=p^k-1const (2.33) получим


Расход газа будет равен

(3.9) где ;

p^*- полное давление, давление торможения



P^*=const

P=const

*



Для получения однозначного значения полного движения принято считать, что торможение потока происходит по изоинтропе, в этом случае так же справедливо уравнение Клапейрона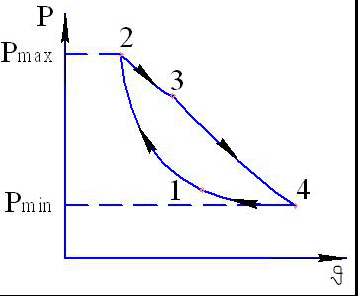



Скорость звука.

Из физики известна ф-ла для определения скорости распределения возмущений в сплошной среде которая совпадает с местной скоростью звука

(3.11)

При адиабатном процессе давление связано с плотностью следующим образом:

PV^k=const; pρ^-k=const; p=ρ^kconst

Подставив (3.12) в (3.11) получим уравнение для определения местной скорости звука в потоке газа



Скорость газа часто определяют с помощью числа маха

Мах (3.14)

При М<1 - до

М=1 - звуковой

М>1 - сверх