Термодинамика. Термоебаника. Закон теплопроводности. Гипотеза Фурье. 4 1 Изображение основных термодинамических процессов на диаграмме pv. 5
 Скачать 3.87 Mb. Скачать 3.87 Mb.
|
Билет 16.Вопросы: 1. Политропный процесс. Коэффициент распределения теплоты. Политропные процессы – это равновесные, обратимые процессы, которые протекают при постоянной теплоемкости c=const. Реальные процессы могут быть приближенно описаны уравнениями для политропных процессов. Политропный процесс состоит в изменении состояния рабочего тела, в котором во внутреннюю энергию в течение всего процесса превращается одна и та же доля количества внешней теплоты. При этом на совершение внешней механической работы приходится доля теплоты, равная: где 2. Стационарная теплопроводность многослойной сферической стенки с граничными условиями 1го рода многослойная не гуглится 3. Как изменится коэффициент теплоотдачи при ламинарном течении, если заменить воду на масло? Изменением теплопроводности жидкости пренебречь, БИЛЕТ 171) (Показатель политропного процесса) Политропными называются ТД процессы, у которых закон распределения энергии характеризуется условием 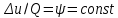 в течение всего процесса. Т.е. основными характеристиками политропного процесса являются уравнения в течение всего процесса. Т.е. основными характеристиками политропного процесса являются уравнения 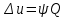 и и 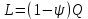 . .Все ранее рассмотренные процессы (Изохорный Изобарный Изотерический Адиабатный) являются политропными, но с явно выраженными внешними признаками в виде 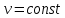 , , 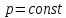 , , 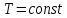 или или 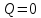 . В общем случае таких признаков может не быть. Политропные процессы подчиняются уравнению . В общем случае таких признаков может не быть. Политропные процессы подчиняются уравнению 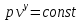 , где , где 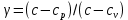 – показатель политропного процесса; – показатель политропного процесса; 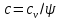 – теплоёмкость политропного процесса. Уравнение политропного процесса – теплоёмкость политропного процесса. Уравнение политропного процесса 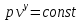 является обобщающим уравнением для всех ТД процессов с постоянным законом распределения энергии, в том числе для ранее рассмотренных. является обобщающим уравнением для всех ТД процессов с постоянным законом распределения энергии, в том числе для ранее рассмотренных.2) (Нестационарная теплопроводность) Нестационарные тепловые процессы сопровождаются не только изменением температурного поля по времени, но почти всегда связаны с изменением энтальпии тела, т. е. с его нагревом и охлаждением. Практические задачи нестационарного теплообмена можно разделить на две основные группы. *К первой относятся процессы, происходящие при переходе тепла из некоторого начального теплового состояния в иное стационарное, обычно равновесное тепловое состояние. Примерами могут служить изменение температурного поля в теле, помещенном в среду, температура которой отличается от начальной температуры тела, или выравнивание температур в теле с заданным начальным распределением температур. *Ко второй группе можно отнести процессы, происходящие в телах, испытывающих тепловое воздействие извне, изменяющиеся во времени по некоторому закону. Здесь можно назвать процессы периодического изменения температуры при движении ИСЗ по орбите, часть которой пролегает в тени Земли, суточные и годовые колебания температуры в верхних слоях земной коры, тепловые режимы аппаратов, находящихся на поверхности Луны, процессы в регенеративных теплообменниках и др. Постановка задачи нестационарной теплопроводности Выведенное дифференциальное уравнение теплопроводности Фурье (Фурье–Кирхгофа) в случае неподвижной среды и отсутствия внутренних источников тепла имеет вид 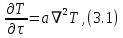 где 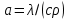 и и 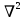 – оператор Лапласа, записанный в прямоугольной, цилиндрической, сферической или иной системах координат. Это уравнение устанавливает зависимость между температурой, временем и координатами тела в элементарном объеме, т. е. связывает временные и пространственные изменения температуры тела. – оператор Лапласа, записанный в прямоугольной, цилиндрической, сферической или иной системах координат. Это уравнение устанавливает зависимость между температурой, временем и координатами тела в элементарном объеме, т. е. связывает временные и пространственные изменения температуры тела.Если заданы форма и размеры тела, а также его физические свойства 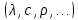 , т.е. геометрические и физические условия однозначности, то для решения уравнения (3.1) необходимо задать еще начальные и граничные, или краевые условия. , т.е. геометрические и физические условия однозначности, то для решения уравнения (3.1) необходимо задать еще начальные и граничные, или краевые условия.Поскольку температура тела в общем случае является функцией координат и времени 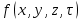 , то начальные условия, т. е. распределение температур в теле в начальный момент, задаются в виде , то начальные условия, т. е. распределение температур в теле в начальный момент, задаются в виде 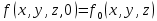 , где , где 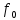 – известная функция, которая необязательно должна быть задана аналитически, а может быть представлена численно или графически. – известная функция, которая необязательно должна быть задана аналитически, а может быть представлена численно или графически.В ряде практических задач начальное условие имеет более простой вид: 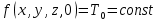 . .Для однородных тел граничные условия могут быть заданы трех видов: температура любой точки поверхности тела в любой момент времени; тепловой поток у поверхности, либо температура среды, омывающей тело; условия теплообмена тела с окружающей средой. В отличие от стационарных задач все величины, входящие в граничные условия, могут изменяться во времени по заданному закону. 3) В трубе течет жидкость при ламинарном режиме течения. Как изменится коэффициент теплоотдачи, если диаметр канала увеличить 3 раза? Каковы будут изменения при турбулентном режиме течения? |
