Термодинамика. Термоебаника. Закон теплопроводности. Гипотеза Фурье. 4 1 Изображение основных термодинамических процессов на диаграмме pv. 5

• Название: Закон теплопроводности. Гипотеза Фурье. 4 1 Изображение основных термодинамических процессов на диаграмме pv. 5
• Анкор: Термодинамика
• Дата: 26.09.2022
• Размер: 3.87 Mb.
• Имя файла: Термоебаника.docx
• Тип: Закон; #697033
• страница: 7 из 11

1)Энтальпия.

Многие термодинамические расчеты облегчаются при использовании аддитивных свойств термодинамических тел, называемых энергетическими или калорическими параметрами состояния (функции состояния, получаемые расчетным путем). Такое название эти параметры состояния получили потому, что в их размерностях присутствует единица энергии [Дж] или [ккал]. С некоторыми из них мы уже познакомились: это энтропия S [Дж/К] и внутренняя энергия U [Дж]. Теперь познакомимся с энтальпией.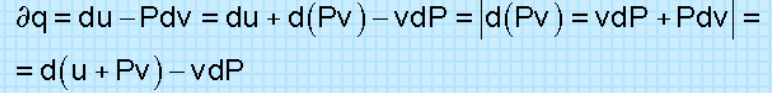

Преобразуем выражение первого закона термодинамики (3.35), записав его в виде

В этом равенстве сумма (u+Рv) является функцией состояния или энергетическим параметром состояния, ее назвали энтальпией и обозначили буквой h [Дж/кг], в переводе с греческого энтальпия - нагреваю, параметр ввел в 1909 г. Г.Камерлинг-Оннесом



В выражении (3.39) h - удельная энтальпия, для всей массы тела полная энтальпия обозначается буквой H [Дж] и рассчитывается как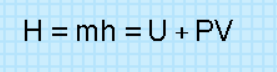

 Полная энтальпия H обладает свойствами аддитивности (суммирования), т.к. внутренняя энергия U и объем V - величины экстенсивные, а давление Р - величина интенсивная. Удельная энтальпия h обладает свойствами интенсивной величины. Энтальпия относится к энергетическим (калорическим) параметрам.

Энтальпия имеет определенный физический смысл. Прокомментируем физический смысл энтальпии с помощью рисунка 3.7. В цилиндре с поршнем находится газ при давлении Р. Давление газа на поршень уравновешивается внешним силовым воздействием F, т.е. система находится в равновесном состоянии. Энергию газа такой системы можно представить в виде суммы двух энергий: внутренней энергии газа - U и потенциальной энергии газа, которая характеризуется работой внешних сил, уравновешивающих давление газа, затраченных на заполнение газом данного объема.

2) Стационарная теплопроводность многослойной стенки с граничными условиями 1^го рода

Р 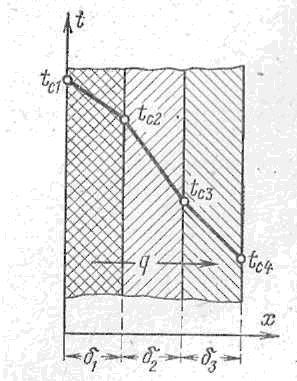ассмотрим стационарную теплопроводность многослойной плоской стенки, каждый слой которой является однородной стенкой, подобной той, которая рассматривалась ранее.

Рис.2.1.3 Многослойная плоская стенка

Предполагается, что общая тол­щина многослойной стенки, равная сумме толщин отдельных слоев, на­много меньше высоты и ширины стенки.

В этом случае изотермиче­скими поверхностями являются пло­скости, параллельные граничным плоскостям (в том числе и плоско­сти стыка между отдельными слоя­ми, рис. 2.1.3). Отдельные слои стен­ки имеют гладкие граничные поверхности, плотно прилегаю­щие друг к другу так, что темпера­туры контактирующих поверхностей равны.

Температура левой граничной поверхности обозначена t_c1, температура на стыке пер­вого и второго слоев— t_c2, температура на стыке второ­го и третьего слоев — t_c3и т. д.

Заданными считаются температуры t_c1и t_c4, толщины отдельных слоев δ₁,δ₂ и δ₃, а также коэффициенты теплопроводности материала каждого слоя λ₁ , λ₂ и λ_3.

 При рассмотрении , теплопроводности однослойной стенки было показано, что плотность теплового потока не изменяется при переходе от одной изотермической поверхности к другой при движении слева направо, т. е. вдоль оси х.

Плоскость стыка между первым и вторым слоями также представляет собой изотермическую по­верхность с тем же значением плотности теплового по­тока, что и в первом слое. Но эта плоскость является «начальной» по отношению ко второму слою, в котором, следовательно, также установится постоянная по толщи­не плотность теплового потока q, равная плотности теп­лового потока в первом слое. Такие же рассуждения справедливы и для всех последующих слоев.

С другой стороны, на каждый слой можно смотреть как на однородную стенку, для которой справедливо выражение, определяющее величину q.

 Запишем это выражение последовательно для всех слоев, начиная с первого: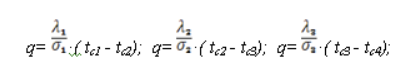

Плотность теплового потока через плоскую стенку :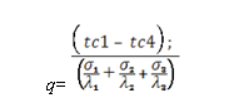

1. 
   Как изменится коэффициент теплоотдачи при турбулентном течении, если заменить воду на масло? Изменением теплопроводности жидкости пренебречь
   

Билет 13.

1. Энтропия.

Энтропия – функция состояния термодинамической системы, не зависящая от пути процесса в системе. Зависит от начального и конечного состояния в системе. Её существование постулируется вторым началом термодинамики. Энтропию можно определить как меру беспорядка в системе и меру необратимого рассеивания энергии.

Формула: dS = dQ/T (отношение порции тепла, получаемого системой, к температуре системы).

В силу второго начала термодинамики, энтропия замкнутой изолированной системы не может уменьшаться, когда в ней протекают обратимые процессы. Но энтропия возрастает, когда в системе протекают необратимые процессы. Переход термодинамической системы от неравновесного состояния к равновесному тоже сопровождается ростом энтропии. В равновесном состоянии энтропия достигает максимума.

Для нахождения изменения энтропии реального необратимого процесса нужно разбить его на стадии, которые проводятся обратимо, вычислить для них изменения энтропия, а затем просуммировать для всех стадий.

2. Стационарная теплопроводность однослойной цилиндрической стенки с граничными условиями 3го рода.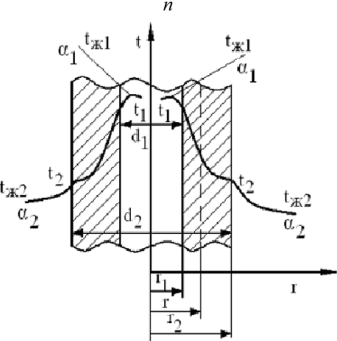

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы. В стационарном режиме теплопередача - величина постоянная, температурное поле не изменяется во времени и зависит только от координат.

Схема процесса для цил.стенки с ГУ третьего рода:

Линейная плотность теплового проходящего через цилиндрическую стенку от греющей жидкости внутри трубы к нагреваемой снаружи, находится по следующим формулам:

• теплоотдача на внутренней поверхности

• распространение теплоты в стенке теплопроводностью

• теплоотдача на внешней поверхности стенки к нагреваемой жидкости

Затем находим разности температур и, складывая их почленно, определяем линейную плотность теплового потока. Полученное по итогам выражение называется линейным коэффициентом теплопередачи (k) для цилиндрической стенки, Вт/(м-К). Линейный коэффициент теплопередачи численно равен количеству теплоты, проходящей в 1 с. через цилиндрическую поверхность длиной 1 м при разности температур между жидкостями 1 К. Величина, обратная линейному коэффициенту теплопередачи называется линейным термическим сопротивлением теплопередачи через цилиндрическую стенку, К/(Вт/м).

Уравнение теплопередачи для цилиндрической стенки приобретает вид



Полное линейное термическое сопротивление теплопередачи является суммой частных сопротивлений теплоотдачи и линейного сопротивления.

3. Как изменится коэффициент теплоотдачи при турбулентном течении, если заменить масло на воду? Изменением теплопроводности жидкости пренебречь,

Билет 14.

1. Средняя и истинная теплоемкость.

Поскольку теплоемкость идеального газа зависит только от температуры, а реального еще и от давления, то в термодинамике различают истинную и среднюю теплоемкости.

Истинная теплоемкость вещества – это теплоемкость при заданной температуре. Определяется как производная от количества теплоты, подводимого к телу в процессе нагрева, по его температуре.

Средняя теплоемкость – это теплоемкость газов в заданном интервале температур. Определяется как отношение количества теплоты к конечной разности температур.

2. Критический диаметр тепловой изоляции.

Тепловой изоляцией называют всякое покрытие горячей поверх­ности, которое способствует снижению потерь теплоты в окружаю­щую среду. Для тепловой изоляции используют материалы с низким коэффициентом теплопроводности ­– асбест, шлаковая или стеклянная вата, пробка и др.

При увеличении диаметра тепловой изоляции термическое сопротивление теплопроводности увеличивается, а термическое сопротивление теплоотдачи уменьшается. Следовательно, при определенном значении диаметра изоляции тепловые потери изолированного трубопровода будут больше, чем неизолированного. Диаметр изоляции, при котором теплопотери максимальны, называется критическим. Для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше наружного диаметра неизолированного трубопровода.

3. Оцените процессы теплообмена при разогреве воды в чайнике на огне. Назовите участок наибольшего термического сопротивления.

Билет 15.

Вопросы:

1. Теплоемкость термодинамического процесса.

Теплоемкость – это количество теплоты, необходимое для нагревания термодинамической системы на один градус по шкале Кельвина.

Теплоемкость системы зависит от:

а) состава и температуры системы;

б) размера системы;

в) условий, при которых происходит переход теплоты.

По количеству нагреваемого вещества различают:

1) удельную теплоемкость Суд, отнесенную к 1 кг или 1 г вещества;

2) молярную (мольную) теплоемкость См, отнесенную к 1 моль вещества.

В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому его теплоемкость зависит от характера термодинамического процесса. Т.к. в зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.

2. Стационарная теплопроводность однослойной сферической стенки с граничными условиями 1го рода. Ебучий вопрос, потому что без листа формул тут никак.









3. Как изменится коэффициент теплоотдачи при турбулентном течении, если заменить воду на масло? Изменением теплопроводности жидкости пренебречь,