Лекции по механике. Законах Ньютона. Поэтому её часто называют Ньютоновской механикой
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
Механика — раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, это вызывающие, основанный на законах Ньютона. Поэтому её часто называют «Ньютоновской механикой». Классическая механика подразделяется на:
Основные понятия механики:
Основные законы механики Принцип относительности Галилея - основной принципом, на котором базируется классическая механика является принцип относительности, сформулированный на основе эмпирических наблюдений Г. Галилеем. Согласно этому принципу существует бесконечно много систем отсчёта, в которых свободное тело покоится или движется с постоянной по модулю и направлению скоростью. Эти системы отсчёта называются инерциальными и движутся друг относительно друга равномерно и прямолинейно. Во всех инерциальных системах отсчёта свойства пространства и времени одинаковы, и все процессы в механических системах подчиняются одинаковым законам. Законы Ньютона Основой классической механики являются три закона Ньютона. Первый закон Ньютона устанавливает наличие свойства инертности у материальных тел и постулирует наличие таких систем отсчёта, в которых движение свободного тела происходит с постоянной скоростью (такие системы отсчёта называются инерциальными). Второй закон Ньютона вводит понятие силы как меры взаимодействия тела и на основе эмпирических фактов постулирует связь между величиной силы, ускорением тела и его инертностью (характеризуемой массой). В математической формулировке второй закон Ньютона чаще всего записывается в следующем виде: 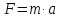 где F —результирующий вектор сил, действующих на тело; a— вектор ускорения тела; m — масса тела. Третий закон Ньютона - для каждой силы, действующей на первое тело со стороны второго, существует противодействующая сила, равная по величине и противоположная по направлению, действующей на второе тело со стороны первого. Закон сохранения энергии Закон сохранения энергии является следствием законов Ньютона для замкнутых систем, в которых действует только консервативные силы. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. Теория машин и механизмов Основные понятия и определения. Теория механизмов и машин занимается исследованием и разработкой высокопроизводительных механизмов и машин. Механизм – совокупность подвижных материальных тел, одно из которых закреплено, а все остальные совершают вполне определенные движения, относительно неподвижного материального тела. Звенья – материальные тела, из которых состоит механизм. Стойка– неподвижное звено.  Стойка изображается . Звено, к которому изначально сообщается движение, называется входным (начальным, ведущим). Звено, совершающее движение, для выполнения которого предназначен механизм – выходное звено. Стойка изображается . Звено, к которому изначально сообщается движение, называется входным (начальным, ведущим). Звено, совершающее движение, для выполнения которого предназначен механизм – выходное звено. Кривошипно- ползунный механизм Если это компрессор, то зв.1 – входное, а зв.3 – выходное. Если это механизм ДВС, то зв.3 – входное, а зв.1 – выходное. Кинематическая пара – подвижное соединение звеньев, допускающее их относительное движение. Все кинематические пары на схеме обозначают буквами латинского алфавита, например A, B, C и т.д. 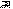  Если , то К.П. – вращательная ; если , то поступательная. Если , то К.П. – вращательная ; если , то поступательная.Порядок нумерации звеньев: входное звено – 1; стойка – последний номер. Звенья бывают:
Например, шатунная группа механизма ДВС. Звенья, соединяясь друг с другом, образуют кинематические цепи, которые разделяют на:
Машина – техническое устройство, в результате осуществления технологического процесса определенного рода, можно автоматизировать или механизировать труд человека. Машины условно можно разделить на виды:
Энергетические машины разделяют на:
Двигатель – техническое устройство, преобразующее один вид энергии в другой. Например, ДВС. Трансформаторная машина – техническое устройство, потребляющее энергию извне и совершающее полезную работу. Например, насосы, станки, прессы. Техническое объединение двигателя и технологической (рабочей машины) – Машинный агрегат (МА). Двигатель имеет определенную механическую характеристику, рабочая машина тоже. 1 – скорость, с которой вращается вал двигателя; 2 – скорость, с которой будет вращаться главный вал рабочей машины. 1 и 2 нужно поставить в соответствие друг другу. Например, число оборотов n1 =7000 об/мин., а n2=70 об/мин. Чтобы привести в соответствие механические характеристики двигателя и рабочей машины, между ними устанавливают передаточный механизм, который имеет свои механические характеристики. uП=1/2=700/70=10 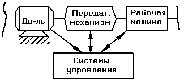 В качестве передаточного механизма могут быть использованы:
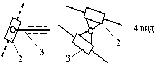
В качестве рабочей машины наиболее часто используют рычажные механизмы. Основные виды рычажных механизмов. 1. Кривошипно-ползунный механизм. а) центральный (рис.1); б) внеосный (дезоксиальный) (рис.2);  е - эксцентриситет Рис. 2 1-кривошип, т.к. звено совершает полный оборот вокруг своей оси; 2-шатун, не связан со стойкой, совершает плоское движение; 3-ползун (поршень), совершает поступательное движение; 4-стойка. 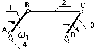 2. Четырехшарнирный механизм. 2. Четырехшарнирный механизм.Звенья 1,3 могут быть кривошипами. Если зв.1,3 – кривошипы, то механизм двукривошипный. Если зв.1 – кривошип (совершает полный оборот), а зв.3 – коромысло (совершает неполный оборот), то механизм кривошипно-коромысловый. Если зв.1,3 – коромысла, то механизм двукоромысловый. 3. Кулисный механизм. 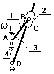 1 - кривошип; 2 - камень кулисы (втулка) вместе с зв.1 совершает полный оборот вокруг А (1 и 2 одно и тоже), а также движется вдоль зв.3, приводя его во вращение; 3 - коромысло (кулиса). 4.Гидроцилиндр (в кинематическом отношении подобен кулисному механизму). 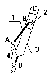 В процессе проектирования конструктор решает две задачи:
Структурный анализ механизма. Понятия о кинематических парах и их классификация. Два звена неподвижно связанных между собой образуют кинематическую пару. Все кинематические пары подвергаются двум независимым классификациям:
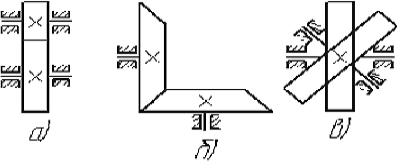
Пара первого класса Пара третьего класса Пара второго класса  Пара четвёртого класса Пара пятого класса  Примеры классификации пар: Пара второго класса:  ; ; 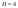 Пара третьего класса: 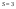 ; ; 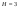 Пара четвёртого класса: 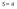 ; ; 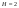 Пара четвёртого класса: 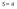 ; ; 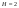 Пара четвёртого класса: 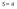 ; ; 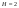 Рассмотрим кинематическую пару «винт-гайка». Число степеней подвижности этой пары 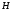 равно 1, а число налагаемых связей равно 1, а число налагаемых связей 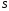 равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим. равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим. Кинематическая цепь – звенья, связанные между собой кинематическими парами различных классов. Кинематическая цепь – звенья, связанные между собой кинематическими парами различных классов.Кинематические цепи бывают пространственными и плоскими. Пространственные кинематические цепи – цепи, звенья которых двигаются в различных плоскостях. Плоские кинематические цепи – цепи, звенья которых двигаются в одной или параллельных плоскостях. Понятия о степени подвижности кинематических цепей и механизмов. Число звеньев свободно парящих в пространстве обозначим за 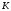 . Для . Для 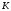 звеньев степень подвижности можно определить по формуле: звеньев степень подвижности можно определить по формуле: 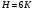 . Образуем из этих . Образуем из этих 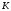 звеньев кинематическую цепь, соединив между собой звенья парами различных классов. Число пар различных классов обозначается за звеньев кинематическую цепь, соединив между собой звенья парами различных классов. Число пар различных классов обозначается за 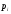 , где , где 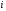 - класс, то есть: - класс, то есть: 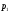 - число пар первого класса, у которого - число пар первого класса, у которого 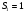 , а , а 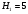 ; ; 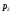 - число пар второго класса, у которого - число пар второго класса, у которого 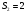 , а , а 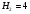 ; ; 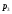 - число пар третьего класса, у которого - число пар третьего класса, у которого 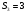 , а , а 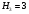 ; ; 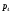 - число пар четвёртого класса, у которого - число пар четвёртого класса, у которого 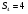 , а , а 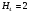 ; ; 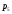 - число пар пятого класса, у которого - число пар пятого класса, у которого 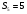 , а , а 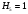 . Степень подвижности образованной кинематической цепи можно определить по формуле: . Степень подвижности образованной кинематической цепи можно определить по формуле: 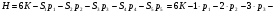 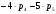 . .Образуем из кинематической цепи механизм. Одним из основных признаков механизма является наличие стойки (корпуса, основания), около которого движутся остальные звенья под действием ведущего звена (звеньев). Степень подвижности механизма принято обозначать за 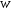 . Одно из звеньев кинематической цепи превратим в стойку, то есть отнимем у него все шесть степеней подвижности, тогда: . Одно из звеньев кинематической цепи превратим в стойку, то есть отнимем у него все шесть степеней подвижности, тогда: 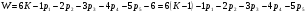 - формула Сомова-Малышева. - формула Сомова-Малышева.В плоской системе максимальное число степеней подвижности 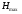 равно двум. Поэтому степень подвижности плоской кинетической цепи можно определить по следующей формуле: равно двум. Поэтому степень подвижности плоской кинетической цепи можно определить по следующей формуле: 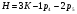 . Степень подвижности плоского механизма определяется по формуле Чебышева: . Степень подвижности плоского механизма определяется по формуле Чебышева: 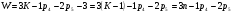 , где , где  - число подвижных звеньев. Используя определение высших и низших кинематических пар формулу Чебышева можно записать следующим образом: - число подвижных звеньев. Используя определение высших и низших кинематических пар формулу Чебышева можно записать следующим образом: 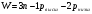 . .Пример определения степени подвижности: 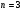 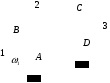 ; ;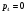 ; ;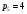 ; ;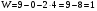 . .Классификация механизмов Количество типов и видов механизмов исчисляется тысячами, поэтому классификация их необходима для выбора того или иного механизма из большого ряда существующих, а также для проведения синтеза механизма. Универсальной классификации нет, но наиболее распространены 3 вида классификации:
Структурные группы для плоских рычажных механизмовУсловие существования любой структурной группы описывается формулой W = 3n – 2P5 = 0. Так как количество звеньев n и количество кинематических пар P5 – целые числа, то 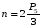 – кратно 2, то есть чётно, – кратно 2, то есть чётно,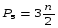 – кратно 3. – кратно 3.Все структурные группы принято разделять на классы – со 2-го по 4-й, в зависимости от числа звеньев, образующих группу, числа поводков в группе 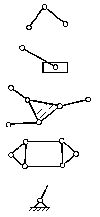 Двухповодковая структурная группа 2-го кл. Структурная группа 2-го кл. Структурная группа 3-го кл. Структурная группа 4-го кл. Механизм 1-го кл. (начальный механизм) Рис. 1.4. Примеры структурных групп При добавлении к механизму 1-го класса различных структурных групп можно получить механизм, состоящий из одной или нескольких структурных групп и механизма 1-го класса. Механизмам присваивается определённый класс, соответствующий наивысшему классу входящих в него структурных групп. 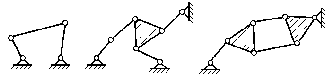 2-й кл. 3-й кл. 4-й кл. Рис. 1.5. Механизмы различных классов Порядок структурной группы равен числу свободных кинематических пар, которыми группа присоединяется к более простому механизму. Свободные пары показаны стрелками. 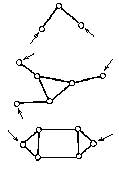 Структурная группа 2-го кл., 2-го порядка Структурная группа 2-го кл., 2-го порядка(все структурные группы 2-го кл. имеют 2-й порядок) Структурная группа 3-го кл., 3-го порядка Структурная группа 4-го кл., 2-го порядка Примеры структурных групп различных классов Наиболее распространённые структурные группы 2-го класса подразделяются на 5 видов.
Примечание. 1 – ведущее звено; 2 и 3 – звенья, образующие структурную группу. Для определения класса механизма его разделяют на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм). От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм, их может быть несколько). По классу структурных групп определяют класс механизма. Количество начальных механизмов равно величине W. Пример разделения плоского рычажного механизма на структурные группы показан на рис. 1.7. Предварительно вычисляют степень подвижности механизма W по формуле W = 3n – 2P5 – P4. В данном случае W = 1, а это значит, что в механизме должны быть одно ведущее звено и соответственно один начальный механизм. 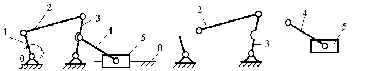 а б в г Разделение механизма на структурные группы: а – исходный механизм; б – начальный механизм; в – 2-й класс, 1-й вид; г – 2-й класс, 2-й вид Избыточные связи В некоторых случаях при проектировании механизмов для повышения жёсткости конструкции, улучшения условий передачи сил вводятся так называемые избыточные (пассивные) связи (дополнительные звенья). Избыточная (пассивная) связь 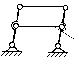 Механизм с избыточной связью В этом случае степень свободы вычисляется по формуле W = 3n – 2P5 + q= 34 - 26 + 1 = 1, где q – число избыточных (пассивных) связей. Лишние степени свободы |
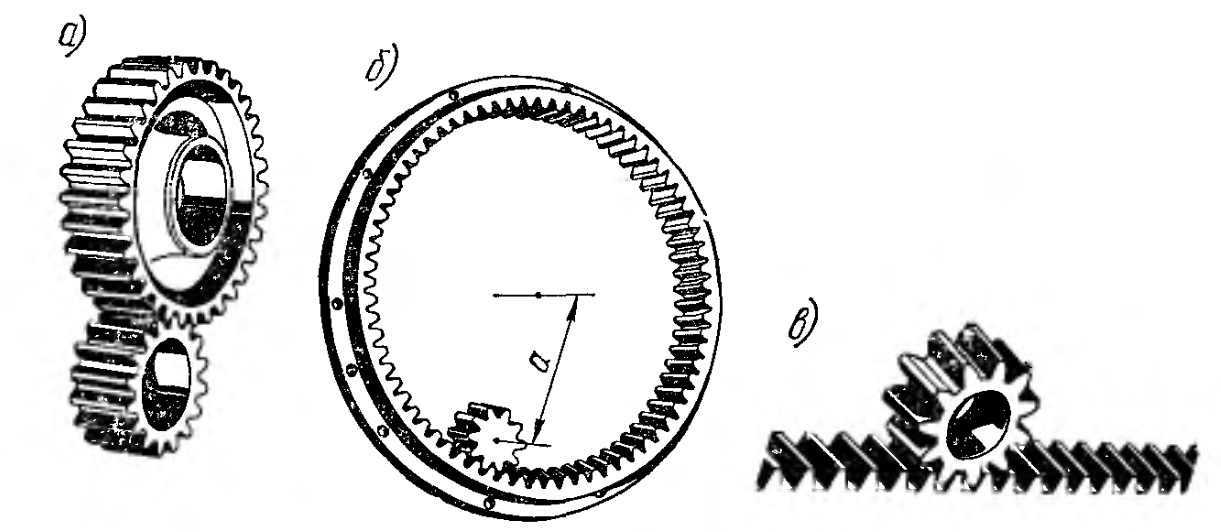
| Пара зубчатых колес с внешним зацеплением: 1, 2 – зубчатые колеса | Пара зубчатых колес с внутренним зацеплением: 1, 2 – зубчатые колеса |
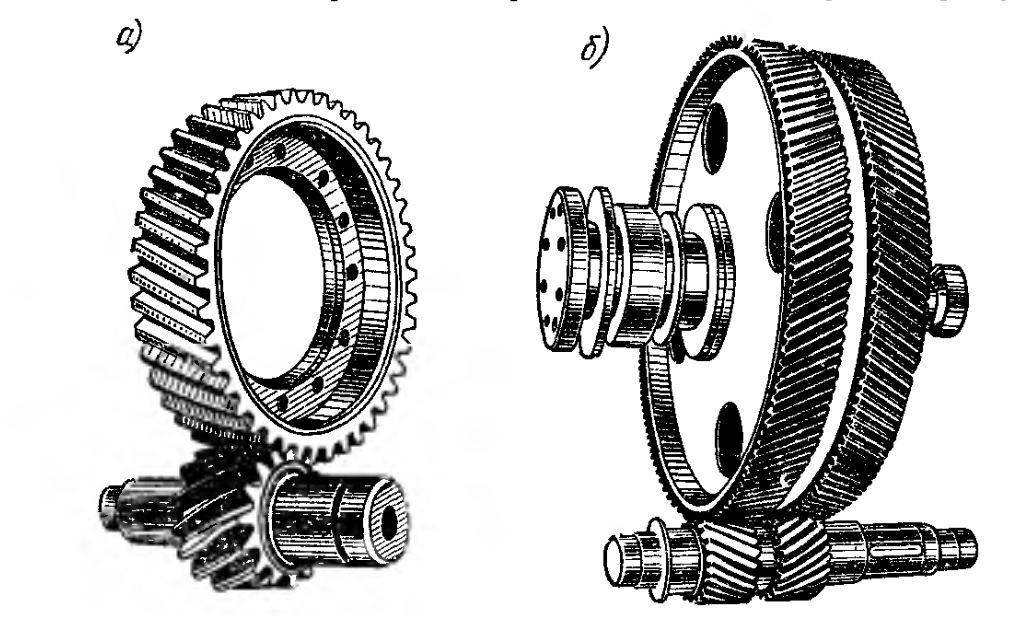
Передаточное отношение сложных (многоступенчатых) зубчатых передач (рис. 5.4) равно произведению передаточных отношений ступеней:
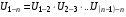 ,
,где
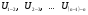 – передаточные отношения ступеней.
– передаточные отношения ступеней.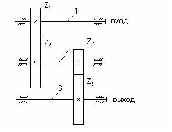
Двухступенчатая зубчатая передача
Например, для двухступенчатой зубчатой передачи, кинематическая схема которой представлена на рис. величина передаточного отношения
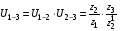 .
.Основные геометрические параметры
зубчатого колеса цилиндрической передачи
Рассмотрим геометрические параметры зубчатого колеса цилиндрической передачи в плоскости, перпендикулярной оси его вращения.
Каждый зуб колеса имеет ось симметрии, проходящую через ось вращения колеса О. Угол между осями симметрии называется угловым шагом τ. Число зубьев колеса z=2π/τ (если τ измеряется в радианах) или z=360º/ τ (если τ измеряется в угловых градусах). Внешняя граница зуба очерчивается окружностью выступов радиусом ra, а внутренняя часть впадины – окружностью впадин радиусом rf.
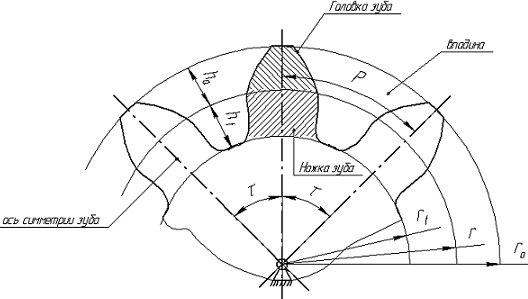
Геометрические параметры зубчатого колеса
Окружность радиусом r делит зуб по высоте на головку и ножку. Расстояние между одноименными профилями соседних зубьев по дуге этой окружности (или между соседними осями симметрии зубьев) называется окружным шагом P.
Длина окружности диаметром d=2 π r
L=Pz= πd,
откуда
d=(P/π)×z.
Величину P/π = m называют модулем. На него введен ГОСТ 9563-60, в соответствии с которым при расчетах геометрических параметров зуб-чатых колес его выбирают из стандартного ряда в пределах m = 0,05…100 мм.
Окружность, по которой модуль m является стандартной величиной, называется делительной окружностью с диаметром d = m×z или радиусом r = (m×z)/2.
Все остальные геометрические параметры зубчатого колеса в соответствии с ГОСТом пропорциональны модулю m:
высота головки зуба ha = m;
высота ножки зуба hf = 1,25 m;
высота зуба h = ha+hf = 2,25 m;
радиус окружности выступов
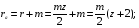
радиус окружности впадин
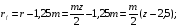
окружной шаг P=π×m;
толщина зуба по делительной окружности
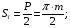
ширина впадин по делительной окружности
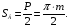
Ширину колеса принимают в пределах в = (10…30)m. Межосевое расстояние двух зацепляющихся колес нулевого зацепления
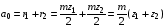 ,
,где r1 и r2 – радиусы делительных окружностей зацепляющих колес;z1 и z2 – число их зубьев.
В зацепление друг с другом могут входить только зубчатые колеса, имеющие одинаковый модуль m и окружной шаг P.

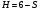 .
.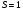 ;
; 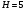 .
.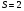 ;
; 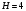 .
.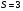 ;
; 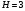 .
.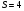 ;
; 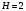 .
.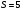 ;
; 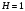 .
.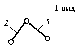
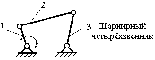

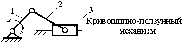





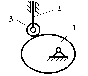
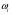 , (1/с), частот вращений
, (1/с), частот вращений 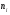 , (об/мин), или обратному отношению количества зубьев колес
, (об/мин), или обратному отношению количества зубьев колес 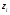 :
: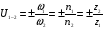 .
.