Законодательная и правовая основа технического нормирования и стандартизации 2
 Скачать 95.1 Kb. Скачать 95.1 Kb.
|
|
В зависимости от последующего влияния на развитие производства можно выделить три вида стандартизации принципиально отличающихся подходами к установлению в стандартах соответствующих норм: стандартизация по достигнутому уровню опережающая стандартизация комплексная стандартизация Стандартизация по достигнутому уровню - стандартизация, устанавливающая показатели, отражающие свойства существующей и освоенной в производстве продукции и таким образом фиксирующая достигнутый уровень производства. Такой подход характерен при стандартизации показателей качества продукции массового производства межотраслевого применения (радиокомпоненты, реле, крепѐжные изделия, некоторые виды сырья и материалов). Опережающая стандартизация заключается в установлении повышенных, по отношению к уже достигнутому на практике уровню, норм, требований к объектам стандартизации, которые согласно прогнозам будут оптимальными в последующее время. При этом, в зависимости от реальных условий, в стандартах могут устанавливаться ступени качества, имеющие дифференциальные показатели, нормы, характеристики и сроки их введения. Таким образом, опережающая стандартизация ставит определенные задачи перед разработчиком и изготовителем продукции, побуждая их к совершенствованию объектов стандартизации, повышению безопасности и улучшению их качества. Комплексная стандартизация - стандартизация, при которой для оптимального решения конкретной проблемы осуществляется целенаправленное и планомерное установление и применение системы взаимосвязанных требований как к самому объекту стандартизации в целом, так и к его основным элементам. При этом комплексная стандартизация призвана обеспечивать разработку и внедрение комплексов взаимосвязанных и согласованных стандартов, охватывающих совокупность требований к объектам стандартизации: изделиям в целом, их составным частям, сырью, материалам, покупным изделиям, технологии изготовления, к упаковке, транспортировке и хранению, эксплуатации и ремонту. Принцип предпочтительности является теоретической базой современной стандартизации и используется при проведении унификации, типизации и при разработке стандартов на изделия широкого применения, решении задач рационального выбора и установления градации количественных значений параметров изделий. Этот принцип основывается на использовании рядов предпочтительных чисел, которые используются для выбора типоразмеров деталей и типовых соединений, рядов допусков, посадок и других параметров, стандартизуемых одновременно для многих отраслей промышленности. ГОСТ 8032 - 84 в соответствии с рекомендациями ИСО устанавливает ряды предпочтительных чисел, определяет их свойства и правила применения. 3.5.3.1 Основные свойстварядовпредпочтительныхчисел Предпочтительные числа получают на основе геометрической прогрессии, i-ый член которого равен i gi 10 R . (3.1) Знаменатель прогрессии 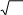 Q R 10 , (3.2) Q R 10 , (3.2)где R = 5, 10, 20, 40, 80, 160, а i принимает целые значения в интервале от 0 до R. Значение R определяет число членов прогрессии в одном десятичном интервале. Предпочтительные числа представляют собой округленные значения членов ряда данной прогрессии. Члены ряда, расположенные в интервале от 1 до 10, составляют исходный ряд. Ряды предпочтительных чисел не ограничиваются в обоих направлениях, при этом предпочтительные числа менее 1 и более 10 получают делением или умножением членов исходного ряда на числа 10, 100, 1000 и т.д. Предпочтительные числа одного ряда могут быть либо только положительными, либо только отрицательными. Произведение или частное двух предпочтительных чисел, а также положительные или отрицательные степени чисел ряда дают предпочтительное число этого же ряда с относительной ошибкой от -1,01% до +1,26%. Куб любого числа ряда R10 в два раза больше куба предыдущего числа, а квадрат в 1,6 раза больше квадрата предыдущего числа с относительной ошибкой до 0,1%. Члены ряда R10 удваиваются через каждые 3 числа, ряда R20 - через каждые 6 чисел, ряда R40 - через каждые 12 чисел и т.д. В рядах, начиная с R10, находится число 3,15, которое , т.е. длины окружностей и площади круга примерно равны предпочтительным числам, если диаметр - предпочтительное число. Ряд R40 включает предпочтительные числа 3000, 1500, 750 и 375, представляющие собой синхронные частоты вращения валов электродвигателей в об/мин. Основные и дополнительные ряды предпочтительных чисел содержат все целые степени десяти. 3.5.3.2 Основныеряды предпочтительных чисел Обозначение и знаменатели предпочтительных чисел приведены в таблице.3.1. Таблица 3.1 Обозначение основного Знаменатель ряда ряда Округлѐнное значение Точное значение Q0 Qт
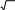 R5 1,6 5 10 R5 1,6 5 10 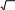 10 10 10 10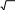 20 10 20 10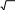 40 10 40 10Основные ряды предпочтительных чисел и их члены в интервале от 1 до 10 представлены в таблице.3.2. При необходимости ограничения основных рядов в их обозначениях указываются предельные члены, которые всегда включаются в ограниченные ряды. Например: R10(1,25...) - это ряд R10, ограниченный членом 1,25 (включительно) в качестве нижнего предела; R20(...45) - ряд R20, ограниченный числом 45 (включительно) в качестве верхнего предела; - R40(75...300 ) - ряд R40, ограниченный членами 75 и 300 и включающий оба члена.
Таблица 3.2
3.5.3.3 Дополнительныерядыпредпочтительныхчисел Обозначения и знаменатели дополнительных рядов приведены в таблице 3.3. Таблица 3.3 Обозначение дополнительного ряда Знаменатель Qо Qт
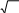 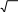 Обозначение ограниченных дополнительных рядов аналогично обозначению ограниченных основных рядов. Обозначение ограниченных дополнительных рядов аналогично обозначению ограниченных основных рядов.3.5.3.4 Выборочные рядыпредпочтительных чисел Выборочные ряды предпочтительных чисел получают отбором каждого второго, третьего, четвѐртого, …, n-ого члена основного или дополнительного ряда начиная с любого числа ряда. Обозначение выборочного ряда состоит из обозначения исходного основного ряда, после которого ставится косая черта и число 2, 3, 4, n - соответственно. Если ряд ограничен, обозначение должно содержать члены, ограничивающие ряд. Если ряд не ограничен, то должен быть указан хотя бы один его член. Например: R5/2(1…1000000) - выборочный ряд состоящий из каждого второго члена основного ряда R5, ограниченный членами 1 и 1000000; R10/3(…80…) - выборочный ряд состоящий из каждого третьего члена основного ряда R10, включающий член 80 и неограниченный в обоих направлениях; R20/4(112…) – выборочный ряд состоящий из каждого четвертого члена основного ряда R20, ограниченный по нижнему пределу членом 112; R40/5(…60) – выборочный ряд состоящий из каждого пятого члена основного ряда R40 и ограниченный по верхнему пределу членам 60. Выборочные ряды предпочтительных чисел должны применятся когда уменьшаются числа градации, создается дополнительный эффект по сравнению с использованием полных рядов, при этом предпочтение следует отдавать рядам, приведенным в таблице 3.4. Использованный выборочный ряд, знаменатели которого равны знаменателям основного ряда, допускается только для установленных значений зависимых параметров. Для выборочных рядов с одинаковыми знаменателями предпочтение следует отдавать ряду, содержащему единицу или число единственной значащей цифрой которых, является 1. Например: 0,01; 0,1; 10; 100 и т.д.
Таблица 3.4
3.5.3.5 Составныерядыпредпочтительныхчисел Составные ряды предпочтительных чисел получают путем сочетания, разложения основных и (или) выборочных рядов. Составной ряд при этом в различных интервалах имеет не одинаковый знаменатель. Количество основных и выборочных рядов используется для получения составного ряда должно быть минимальным. Конечные и начальные члены смежных рядов, образующих составной ряд должны быть одинаковыми. Например:R20(1…2)R10(2…10)R5/2(10…1000) Составные ряды предпочтительных чисел должны применятся, если требуемая плотность значений параметра в рассматриваемом интервале не одинакова. 3.5.3.6 Арифметические предпочтительные рядычисел Арифметические предпочтительные ряды чисел получают на основе арифметической прогрессии, i-ый член которой определяется выражением: 10m аi a0 10m l0 gi a0 R i . (3.3) 10m Это выражение справедливо при условиях, когда a0  10m 10m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
