01 Пр Основные операторы R. Занятие 01. Введение в r содержание установка пакета 1
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
Ввод данных с клавиатуры в RДля ввода данных через консоль можно воспользоваться функцией readline(), которая будет ожидать пользовательский ввод и нажатие клавиши Enter, после чего вернет введенные данные в виде строки. Предположим, пользователь вызывает эту функцию и вводит с клавиатуры 1024: a = readline() Выведем результат на экран: a ## [1] "1024" Функция readline() всегда возвращает строку, поэтому если вы ожидаете ввод числа, полученное значение необходимо явным образом преобразовать к числовому типу. Полезной особенностью readline() является возможность указания строки запроса при вызове функции: lat = readline('Введите широту точки:') ## Введите широту точки: ## 54 lat ПРАКТИЧЕСКИЕ ЗАДАНИЯЗадание 1. Вычислить с точностью не более четвертой цифры после запятой выражение 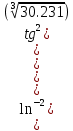 . .Решение. Разумеется, нам не следует сразу же бросаться набирать этого «крокодила» в строке. Надежнее всего разбить данное выражение на небольшие части, сохранить промежуточные вычисления в новых переменных и потом уже образовать ответ: 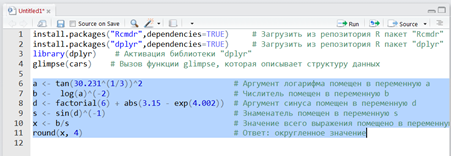 Здесь мы образовали новые переменные 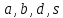 и и 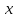 , а в качестве символа присваивания использовали конструкцию, напоминающую стрелку: «<-». Не было бы ошибкой использовать и обычный знак равенства, но тем, кто хочет демонстрировать заграничной публике высший класс следует использовать в этом контексте именно сочетание «<-» или в другую сторону «->» для случая, когда переменная находится справа от присваиваемого выражения. , а в качестве символа присваивания использовали конструкцию, напоминающую стрелку: «<-». Не было бы ошибкой использовать и обычный знак равенства, но тем, кто хочет демонстрировать заграничной публике высший класс следует использовать в этом контексте именно сочетание «<-» или в другую сторону «->» для случая, когда переменная находится справа от присваиваемого выражения.Обратите внимание, что значения наших промежуточных переменных отобразились в правом верхнем окне окружения. Если значений так много, что они не помещаются в данное окно, то узнать значение интересуемой переменной можно и по-другому. Как вариант просто написать ее на свободной строке и нажать Ctrl+Entr: x либо указать ее через точку с запятой с основным выражением: x <- b/s ; x # Значение всего выражения помещено в переменную x либо выделить мышкой именно эту переменную в тексте кода и также отправить на компиляцию Ctrl+Entr (или кликнуть по кнопке Run): 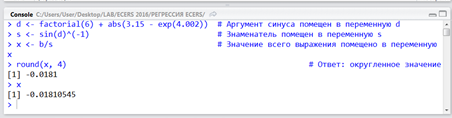 Задание 2. Вычислить выражение с точностью в 3 цифры после запятой 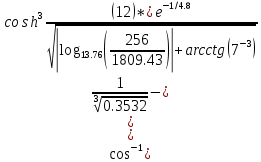 Задание 3. Образовать и вывести на экран векторы a(1,1,2) и b(0, −4,3). Вычислить выражение: a) −4𝑎 + 5𝑏 b) 2(𝑎, 𝑏) ∗ 𝑎 − 3|𝑏| ∗ 𝑏 Задание 4. Образовать и вывести на экран векторы a(2,0, −3) и b(6,1,4). Вычислить их длины и скалярное произведение. Ортогональны ли векторы? Задание 5. Образовать и вывести на экран векторы a(1,1,2,2,3,3,4,4) и b(−2, −1,0,1,2,3,4,5). Какой вектор длиннее? Определить тупой, острый или прямой угол образован между векторами и найти его косинус. Задание 6. Выбрать из матрицы A вектор-столбец максимальной длины, если матрица имеет вид:  Найти угол в градусах между двумя любыми векторами из приведенной матрицы. Задание 7. В R есть встроенные данные о зависимости скорости автомобилей от тормозного пути (исследование Ford, 1920 год). Эти данные хранятся в зарезервированной переменной под именем «cars». Для того, чтобы понять, как хранятся данные о скоростях и дистанциях тормозных путей в cars требуется запустить команду glimpse(cars), которая входит в библиотеку dplyr. Решение Фактически нам необходимо сделать три небольшие операции: Загрузить на компьютер библиотеку dplyr (это очень удобная и популярная библиотека для манипуляций с различными данными): install.packages("dplyr",dependencies=TRUE) # Загрузить из репозитория R пакет "dplyr" Активизировать эту библиотеку в текущей сессии: library(dplyr) # Активация библиотеки "dplyr" Вызвать соответствующую функцию из пакета: ca # Вызов функции glimpse, которая описывает структуру данных Далее мы выделяем эти три набранные строки левой клавишей мыши и запускаем код на компиляцию, щелкнув мышкой по клавише Run (или нажав Ctrl+Enter): В результате в окне консоли получим полную информацию о переменной Observations: 50 Variables: 2 $ speed $ dist из которого следует, что переменная cars представляет собой массив данных (более точно таблицу данных – тип data.frame, но сути это не меняет): «Оbservations: 50» дословно означает «Наблюдений 50 штук» и, если представлять себе эти данные как таблицу, то речь идет о 50 строках; «Variables: 2» дословно означает «Переменных 2 штуки» и фактически это – количество столбцов; «$ speed 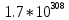 , все что превосходит этот рубеж обозначается в R символом бесконечности «Inf» (не правда ли, сложно себе представить реальное количество чего-либо, выраженное единицей с 308 нулями); , все что превосходит этот рубеж обозначается в R символом бесконечности «Inf» (не правда ли, сложно себе представить реальное количество чего-либо, выраженное единицей с 308 нулями);«$ dist Иными словами, данные о скорости и соответствующей дистанции сгруппированы в двух столбцах, а по строчкам соответствуют одному и тому же наблюдению (конкретной испытуемой машине). В R это означает, что можно обратиться к различным наблюдениям, собранным в объекте cars, следующими способами: cars # Сам объект-массив, вывод на экран консоли cars$speed # Массив скоростей (вектор) cars[ ,1] # То же самое (значения всех строк из первого столбца) cars$dist # Массив тормозных путей (вектор) cars[ ,2] # То же самое (значения всех строк из второго столбца) cars[1, ] # Первое наблюдение (значения всех столбцов из 1-ой строки) cars[23,] # 23-е наблюдение (значения всех столбцов из 23-тьей строки) cars[6,1] # Скорость при 6-ом наблюдении cars$speed[6] # То же самое cars[5,2] # Тормозной путь при 5-ом наблюдении cars$dist[5] # То же самое Сравните построчечно выводы на консоли R, запустив каждую строку в отдельности Ctrl+Enter. Задание 8. Вычислить среднюю скорость первых пяти наблюдений в объекте cars. Решение. В свободной строке составим код, вычисляющий среднее арифметическое первых пяти скоростей: (cars$speed[1] + cars$speed[2] + cars$speed[3] + cars$speed[4] + cars$speed[5])/5 или короче (cars[1,1] + cars[2,1] + cars[3,1] + cars[4, 1] + cars[5,1])/5 # То же самое или еще короче mean(cars[1:5,1]) # То же самое или так mean(cars$speed[1:5]) # То же самое Последние две команды вызывают встроенную функцию вычисления среднего арифметического (mean) для элементов первого столбца (speed) массива cars, взятых из строк с 1-ой по 5-ую включительно. Задание 9. Вычислить среднее арифметическое значение длины тормозного пути для данных cars, выраженное в метрах. Использовать: в 1 футе 0,3048 метра. |
