01 Пр Основные операторы R. Занятие 01. Введение в r содержание установка пакета 1
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
Операторы присваиванияЭти операторы используются для присвоения значений векторам.
Векторная алгебраРассмотрим операции векторной алгебры на примере трех векторов: a <- c(2, -3, 4, 1) # Сформировать вектор a из набора чисел 2, -3, 4, 1 b <- c(-6, 9, -12, -3) # Сформировать вектор b из набора чисел -6, 9, -12, -3 p <- c(3, 2, -1, 4) # Сформировать вектор a из набора чисел 3, 2, -1, 4 a; b; p # Смотрим результат [1] 2 -3 4 1 [1] -6 9 -12 -3 [1] 3 2 -1 4 Основные операции векторной алгебры:  a) вычислить 2𝑎⃗ − 3𝑏⃗ + 𝑝⃗ Для вычисления подобных выражений, называемых линейными комбинациями из-за того, что векторы складываются друг с другом и/или умножаются на числа, достаточно просто записать аналогичную строчку в R: 2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации > 2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации векторов [1] 25 -31 43 15 b) вычислить 𝑎⃗ ∙𝑏⃗ (скалярное произведение векторов) В отличие от предыдущего пункта, здесь нельзя составить обычное умножение векторов, т.к. компилятор R покоординатно перемножит векторы, что не является скалярным произведением. Скалярное произведение векторов: В результате получается не вектор, а число (скаляр) – отсюда и название скалярное произведение. Желая подчеркнуть эту разницу в линейной алгебре часто используют круглые скобки для обозначения скалярного произведения: 𝑎⃗ ∙𝑏⃗⃗ = (𝑎⃗;𝑏⃗⃗). В языке R эти два приёма программируется следующим образом: a*b # Покоординатное произведение векторов (не скалярное произведение!) l # Скалярное произведение векторов с результатом: > a*b # Покоординатное произведение векторов [1] -12 -27 -48 -3 > a%*%b # Скалярное произведение векторов [,1] [1,] -90 Обратите внимание, что результат скалярного произведения представлен в виде матрицы 1 × 1, т.к. в языке R эта операция интерпретируется как частный случай произведения специальных матриц. Если мы не хотим видеть результат в виде матрицы, мы можем вывести его как обычное число: as.numeric(a%*%b) > as.numeric(a%*%b) # Скалярное произведение векторов [1] -90 Аналогично получим скалярное произведение 𝑎⃗ ∙ 𝑝⃗: > as.numeric(a%*%p) # Скалярное произведение векторов [1] 0 Кстати, в последнем случае результат оказался равным нулю, что говорит об ортогональности (перпендикулярности) векторов 𝑎⃗ и 𝑝⃗. d) вычислить |𝑎⃗|, |𝑏⃗⃗| и |𝑝⃗| (длина вектора) Длиной вектора называют число, равное квадратному корню из (𝑎⃗)2 и по смыслу это число является длиной отрезка, соединяющего начало и конец вектора, если его интерпретировать как направленный отрезок в евклидовой геометрии: 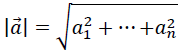 В языке R получить данное выражение можно несколькими способами. Первый из них – вызвать специальную функцию вычисления нормы элемента для вектора: norm(a, type="2") с результатом: > norm(a, type="2") # Длина вектора a (обычная евклидова [1] 5.477226 Второй способ – образовать, согласно формуле, корень из суммы квадратов элементов: sqrt(sum(a^2)) с тем же результатом: > sqrt(sum(a^2)) # Альтернатива: длина вектора a [1] 5.477226 Аналогично получаем для оставшихся векторов: norm(b, type="2") # Длина вектора b (обычная евклидова) sqrt(sum(p^2)) # Альтернатива: длина вектора p e) Вычислить cos (a,b) (Косинус угла между векторами) Воспользуемся формулой для косинуса угла между арифметическими векторами: 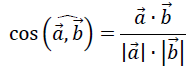 (a%*%b)/(norm(a, type="2")*norm(b, type="2")) # Косинусугламежду a и b с результатом > (a%*%b)/(norm(a,type="2")*norm(b,type="2")) [,1] [1,] -1 Обратим внимание, что косинус оказался равным –1, что говорит об угле между векторами, равном 𝜋. Это означает, что векторы коллинеарны (параллельны) и противоположно направлены. Кстати, это можно было заметить изначально, т.к. координаты векторов пропорциональны с отрицательным коэффициентом: 𝑏⃗= −3𝑎⃗. |
