Статистика. Занятие 1 Тема Сводка и группировка статистических данных Методические указания по теме
 Скачать 179.36 Kb.
|
Практическое занятие 5Тема 5. Ряды динамики Методическиеуказанияпо теме Задача1. Смертность от болезней системы кровообращения в России за период 2002-2011 гг. характеризуется следующим рядом динамики.
Вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Решение. Любое изменение уровней ряда динамики определяется базисным (сравнение с первым уровнем) и цепным (сравнение с предыдущим уровнем) способами. Оно может быть абсолютным (разность уровней ряда) и относительным (соотношение уровней). Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда (36), а цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда (37). YБ YЦ Yi Yi Y1 . Yi1 . (36) (37) По знаку абсолютного изменения делается вывод о характере развития явления: при Y > 0 — рост, при Y < 0 — спад, при Y = 0 — стабильность. В нашей задаче эти изменения определены в 3-м и 4-м столбцах таблицы Ошибка! Источник ссылки не найден.. Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. В нашей задаче это правило выполняется: YЦ=124,2 и Б Y 2010 =124,2. Базисное относительное изменение представляет собой соотношение конкретного и первого уровней ряда (38), а цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда (39). 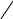 Y iБ Yi. 1 (38) 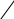 Y iЦ Yi. i1 (39) Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место рост явления, меньше ее — спад, а при равенстве единице наблюдается стабильность явления. В нашей задаче эти изменения определены в 5-м и 6-м столбцах таблицы 3. Вычитая единицу из относительных изменений, получают темп измененияуровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место рост явления, при отрицательном спад, а при нулевом темпе изменения наблюдается стабильность явления. В нашей задаче темпы изменения определены в 7-м и 9-м столбцах таблицы 3, а в 8-м и 10-м сделан вывод о характере развития изучаемого явления. Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему 2010 базисному. В нашей задаче это правило выполняется: iЦ=1,107 и iБ=1,107. Таблица 3 - Вспомогательные расчеты для решения задачи
(см. рис.3): 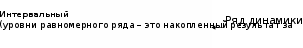  Обобщенной характеристикой ряда динамики является среднийуровень рядаy . Способ расчета yзависит от того, моментный ряд или интервальный 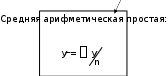 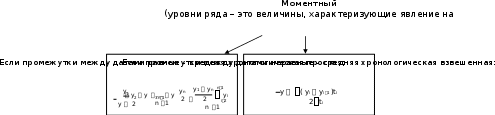 Рис.3. Методы расчета среднего уровня ряда динамики. В нашей задаче ряд динамики интервальный, значит, применяем формулу средней арифметической простой (19): y = 12070,2 / 10 = 1207,02 (тыс. чел.). То есть за период 2001-2010 в России в среднем за год от болезней системы кровообращения умирало 1207,02 тыс. чел. Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения. Базисное среднее абсолютное изменение – это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (40). Цепное среднее абсолютное изменение уровней ряда – это частное от деления суммы всех цепных абсолютных изменений на количество изменений (41). YБ YЦ YБ = n. n 1 YЦ =. n 1 (40) (41) По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными. В нашей задаче Y= 124,2/9 = 13,8, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 13,8 тыс. чел. 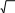 Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (42), а цепное среднее относительное изменение – по формуле (43):iБ=n1 iБ= n1 Yn. Y 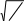 1 (42) n п  iЦ=n1 iЦ. (43) Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или  стабильность. В нашей задаче i= = 1,0114, то есть ежегодно в среднемсмертность от болезней системы кровообращения растет в 1,0114 раза. Вычитанием 1 из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашей задаче T= 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%. Заданияпотемедляпрактическоговыполнения По статистическим данным по России за 2005 – 2010 гг. вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||