Лекция 14. Занятие №8. Занятие 8 ( Лисичкин В. Т., Соловейчик И. Л. Математика) Раздел Линейная алгебра Тема Матрицы, определители Обратная матрица. Матричные уравнения 2го типа
 Скачать 496.64 Kb. Скачать 496.64 Kb.
|
Занятие №8 (Лисичкин В.Т., Соловейчик И.Л. Математика)Раздел 1. Линейная алгебраТема 1.1. Матрицы, определители Обратная матрица. Матричные уравнения 2-го типа. Обратная матрицаРассмотрим обычное простейшее уравнение 2х=4. Известно, что для его решения необходимо разделить обе части этого уравнения на 2. Деление на 2 можно представить как умножение на число 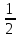 , которое, в свою очередь, может быть записано как , которое, в свою очередь, может быть записано как 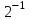 : : 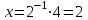 . Число . Число 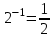 называется числом, обратным к числу 2, поскольку в произведении эти числа дают 1. В общем случае уравнение называется числом, обратным к числу 2, поскольку в произведении эти числа дают 1. В общем случае уравнение 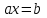 решается умножением обеих частей уравнения на число решается умножением обеих частей уравнения на число 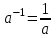 (если (если 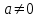 ), которое называется обратным к числу ), которое называется обратным к числу 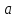 и определяется как число, дающее в произведении с и определяется как число, дающее в произведении с 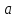 число 1: число 1: 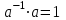 . Таким образом, . Таким образом, 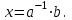 Напомним, что обратное число Напомним, что обратное число 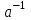 существует для всех чисел существует для всех чисел 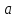 , кроме , кроме 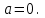 Сейчас мы по аналогии с обратным числом введем понятие обратной матрицы, которое нам поможет решать уже не одно уравнение, а целые системы уравнений определенного вида. Сейчас мы по аналогии с обратным числом введем понятие обратной матрицы, которое нам поможет решать уже не одно уравнение, а целые системы уравнений определенного вида. Матрица 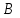 называется обратной матрицей для квадратной матрицы называется обратной матрицей для квадратной матрицы 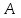 , если , если 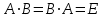 . Отметим, что в этом определении обратной матрицы недостаточно требовать, чтобы произведение матриц Aи B в каком-либо одном порядке давало единичную матрицу, так как для матриц нет гарантии, что произведение этих матриц в другом порядке тоже даст единичную матрицу (в общем случае, как мы уже убеждались, . Отметим, что в этом определении обратной матрицы недостаточно требовать, чтобы произведение матриц Aи B в каком-либо одном порядке давало единичную матрицу, так как для матриц нет гарантии, что произведение этих матриц в другом порядке тоже даст единичную матрицу (в общем случае, как мы уже убеждались, 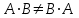 ). ). Из определения следует, что обратная матрица B будет квадратной матрицей того же порядка, что и матрица A (иначе, как легко убедиться, одно из произведений 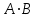 или или 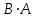 было бы не определено). Обратная матрица для любой матрицыA единственна (если существует) и обозначается было бы не определено). Обратная матрица для любой матрицыA единственна (если существует) и обозначается 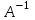 по аналогии с обратными числами. Таким образом, если по аналогии с обратными числами. Таким образом, если 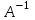 есть матрица, обратная к матрице A , то выполняется: есть матрица, обратная к матрице A , то выполняется: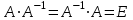 . .Для всех ли обратных матриц существуют обратные? Как было сказано раньше, даже не для всех чисел существует обратное: для числа 0 обратного нет. Похожая ситуация наблюдается и с матрицами. Матрица называется вырожденной, если ее определитель = 0 и для такой матрицы обратной не существует. Справедлива следующая теорема: Теорема. Обратная матрица для квадратной матрицы A вида (2) существует тогда и только тогда, когда матрица A невырожденная. В этом случае обратная матрица единственна и представляется в виде (5) 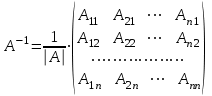 , ,где 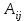 − алгебраические дополнения элементов − алгебраические дополнения элементов 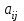 исходной матрицы. исходной матрицы. Формула (5) обосновывает следующий алгоритм вычисления обратной матрицы (на примере матрицы размера 3х3) для матрицы А = 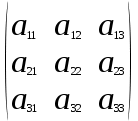 . .1. Вычисляем определитель матрицы D= 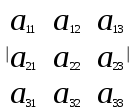 . . 2. Вычисляем алгебраические дополнения всех ее элементов 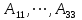 . .3. Составляем так называемую «союзную» матрицу, заменяя элементы исходной матрицы их алгебраическими дополнениями и транспонируя получившуюся матрицу: 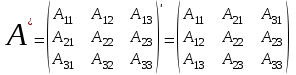 4. Составляем обратную: 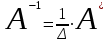 Пример. Найти обратную для матрицы 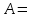 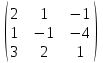 . .Решение. Воспользуемся тем, что ранее для этой матрицы уже были вычислены определитель и алгебраические дополнения всех элементов. Поэтому результаты первых двух пунктов приведенной выше схемы уже есть. 1. D= 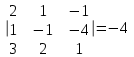 . . 2. А11=7, А12= –13, А13=5, А21= –3, А22=5, А23= –1, А31= –5, А32=7, А33= –3 . 3. «Союзная» матрица : 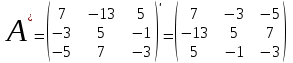 4. Составляем обратную: 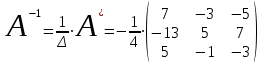 Ответ: 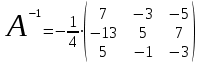 . .Можно было произвести умножение числа 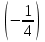 на матрицу и получить обратную матрицу в обычном матричном виде на матрицу и получить обратную матрицу в обычном матричном виде 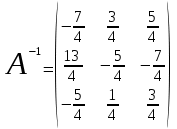 . При этом матрица уже не выглядит столь компактно, да и дальнейшие действия с ней (например, при решении систем линейных уравнений) производить уже не столь удобно. Поэтому обычно обратную матрицу оставляют в том виде, в котором она дана в Ответе. . При этом матрица уже не выглядит столь компактно, да и дальнейшие действия с ней (например, при решении систем линейных уравнений) производить уже не столь удобно. Поэтому обычно обратную матрицу оставляют в том виде, в котором она дана в Ответе.!!! Наиболее просто искать по приведенной схеме обратную матрицу для матриц второго порядка. Пусть дана в общем виде матрица второго порядка 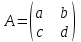 . Построим обратную матрицу по приведенной выше схеме. . Построим обратную матрицу по приведенной выше схеме. 1. D= 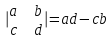 . . 2. 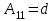 , , 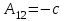 , , 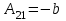 , , 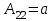 . .3. 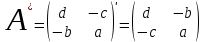 . .4. 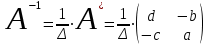 . .Таким образом, обратная для матрицы второго порядка 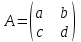 имеет вид: имеет вид:(5а) 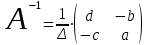 , где , где 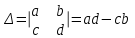 . . Пример 1. Найти для матрицы 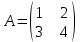 обратную матрицу. обратную матрицу.Решение. Определитель 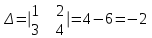 . По формуле (5а) . По формуле (5а)(5б) 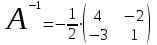 . .Пример 2. Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной, если это возможно 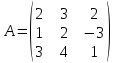 . .Решение: Вычисляем определитель матрицы: 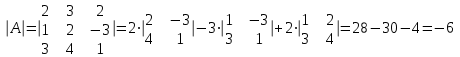 . .|A| 0 матрица имеет обратную ей матрицу. Находим алгебраические дополнения элементов этого определителя: 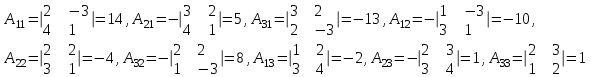 Таким образом: 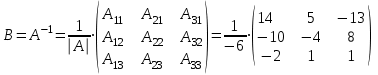 . .Ответ: 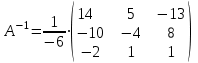 . .Пример 3. Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной, если это возможно 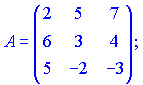 Решение: Вычисляем определитель матрицы 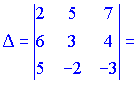 Находим матрицу алгебраических дополнений 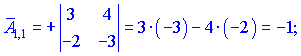 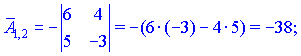 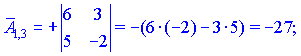 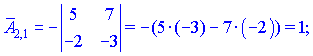 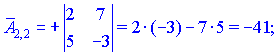 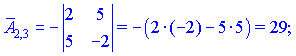 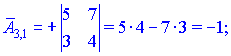 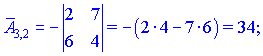 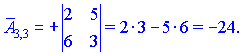 Конечный вид матрицы дополнений 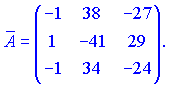 Транспонируем ее и находим союзную матрицу 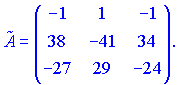 Находим обратную матрицу 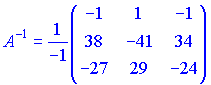 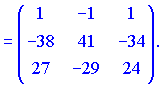 Пример 4.Найдем обратную матрицу для 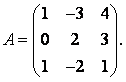 Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения: 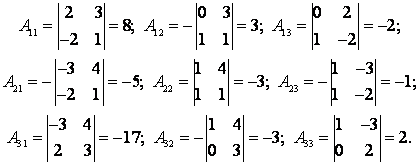 Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце), 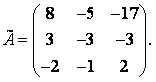 Поскольку |A| = 1· A11 + 0· A12 + 1· A13 = - 9, получаем: 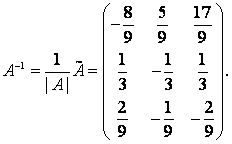 Пример 5. Найти обратную матрицу для 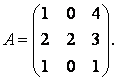 Решение. Проверим невырожденность матрицы А: Следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:  Построим присоединенную матрицу: 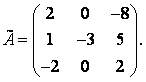 Используя теорему 3.3, находим обратную матрицу:  Решение матричных уравненийМатричные уравнения могут иметь вид: АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица. Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы. Например, чтобы найти матрицу Тогда: Следовательно, чтобы найти решение Аналогично решаются другие уравнения. 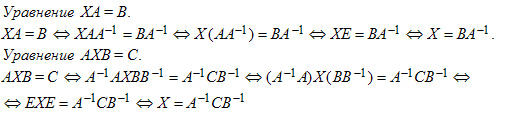 ПРИМЕРЫ: Решить матричные уравнения. 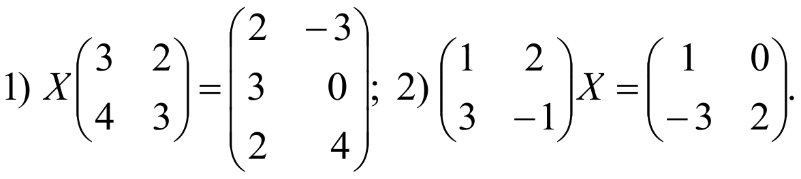 РЕШЕНИЕ: 1) Пусть 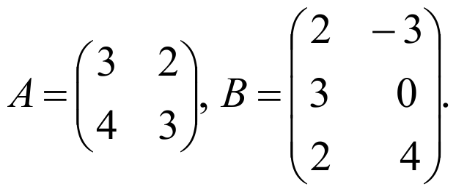 Тогда нам дано уравнение вида ХА=В, следовательно Х=ВА-1. Найдем A-1 . 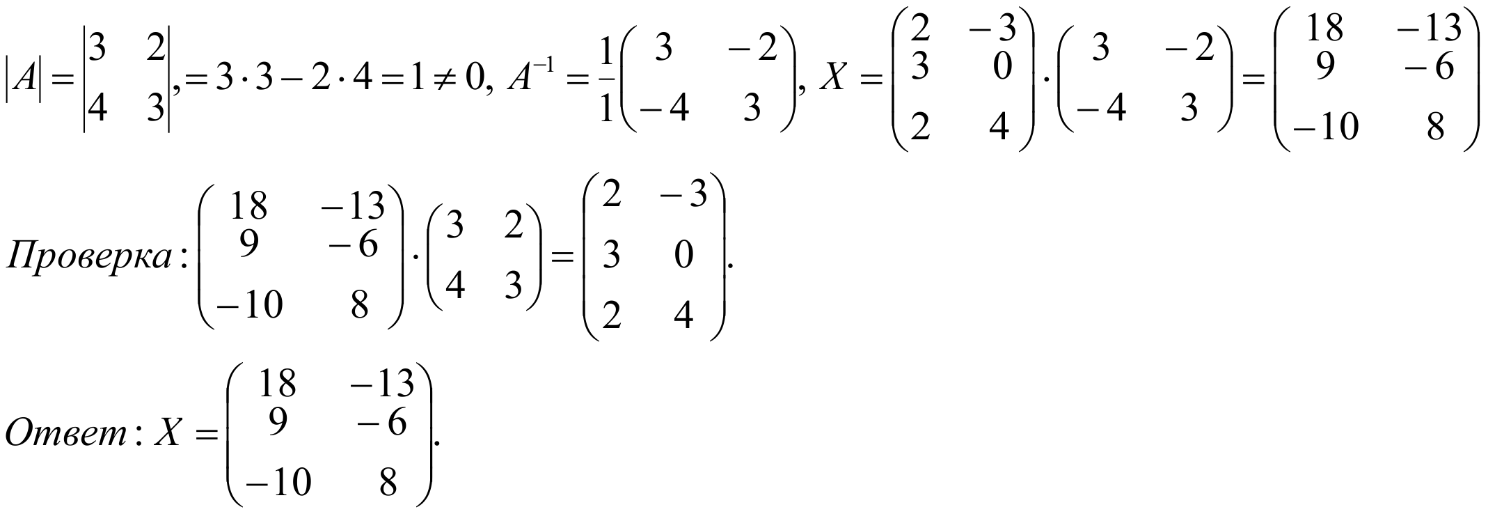 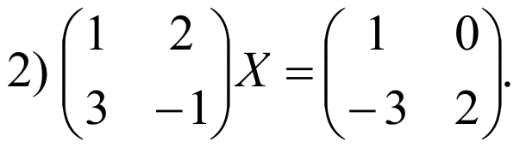 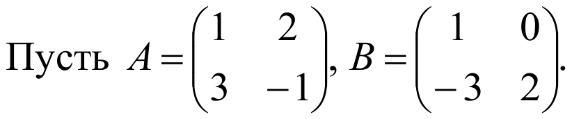 Тогда нам дано уравнение вида АX=В, следовательно Х=А-1B. Найдем A-1 . 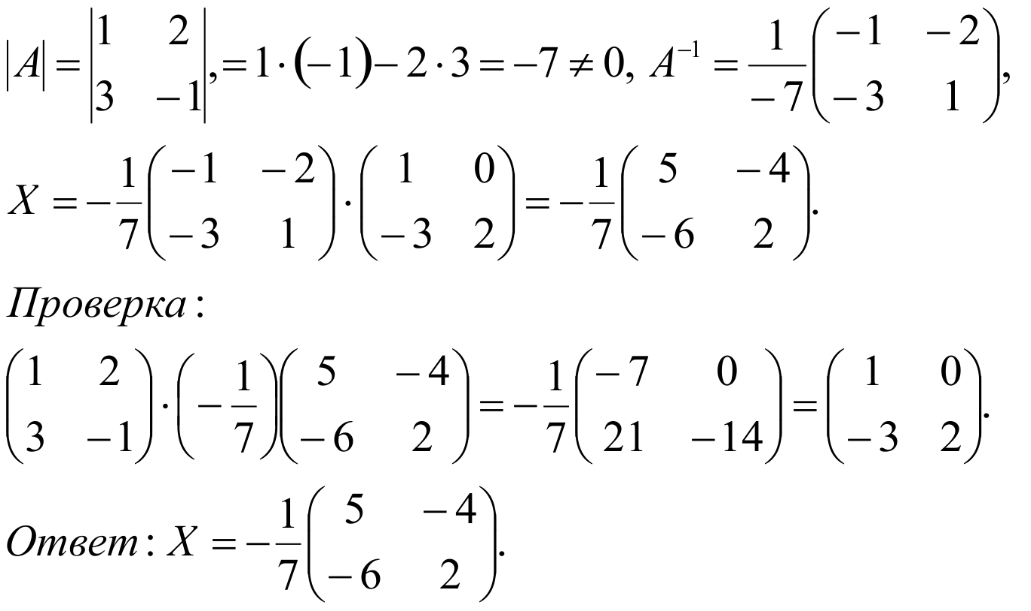 Пример 3. Решить матричное уравнение . 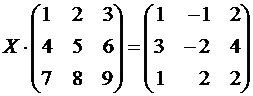 Р 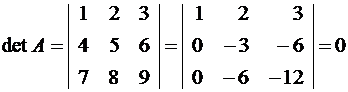 ешение. (в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет. ешение. (в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет.Пример 4. Решить матричные уравнения и сделать проверку. 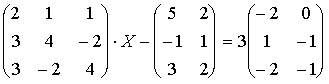 Решение Запишем данное матричное уравнение в матричной форме: A·X - B = 3C. Его можно записать как A·X = 3C + B. Найдем сумму матриц:
Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B. Вычислим определитель матрицы А: ∆ = 2*(4*4 - (-2)*(-2)) - 3*(1*4 - (-2)*1) + 3*(1*(-2) - 4*1) = -12 Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B. Найдем обратную матрицу A-1. Алгебраические дополнения ∆1,1 = (4*4 - (-2)*(-2)) = 12 ∆1,2 = -(3*4 - (-2)*3) = -18 ∆1,3 = (3*(-2) - 4*3) = -18 ∆2,1 = -(1*4 - 1*(-2)) = -6 ∆2,2 = (2*4 - 1*3) = 5 ∆2,3 = -(2*(-2) - 1*3) = 7 ∆3,1 = (1*(-2) - 1*4) = -6 ∆3,2 = -(2*(-2) - 1*3) = 7 ∆3,3 = (2*4 - 1*3) = 5 Обратная матрица A-1.
Матрицу Х ищем по формуле: X = A-1·B
Ответ:
Домашнее задание Л3, стр. 105-108, №1 (Пехлецкий И.Д.) Л4, стр. 71-81, № 56; 58; 60 (Лисичкин В.Т., Соловейчик И.Л.) №56. Найти матрицу, обратную к заданной  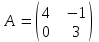 №58. Найти матрицу, обратную к заданной  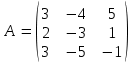 №60. Решить матричные уравнения: 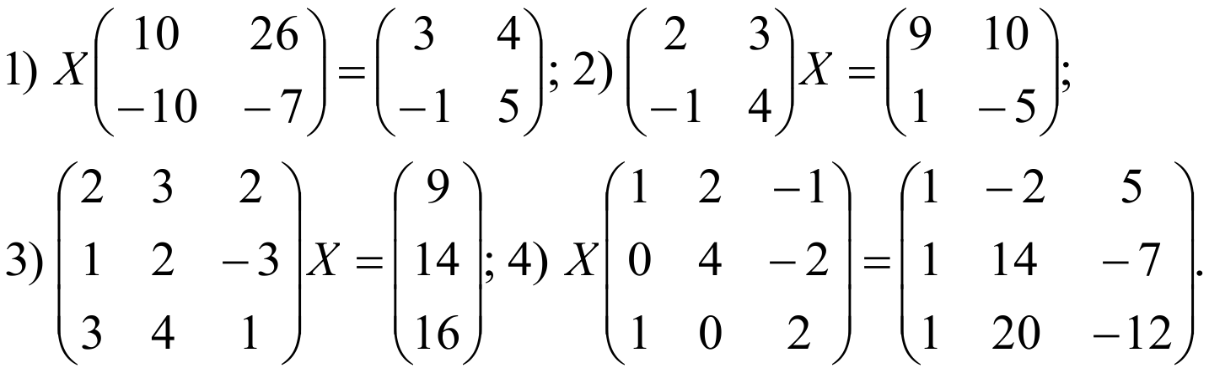 Решение домашнего задания №56. Найти матрицу, обратную к заданной  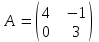 , , 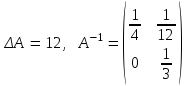 №58. Найти матрицу, обратную к заданной  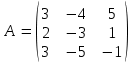 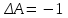 А11 = 8 А12 = 5 А13 = -1 А21 = -29 А22 = -18 А23 = 3 А31 = 11 А32 = 7 А33 = -1
№60. Решить матричные уравнения: 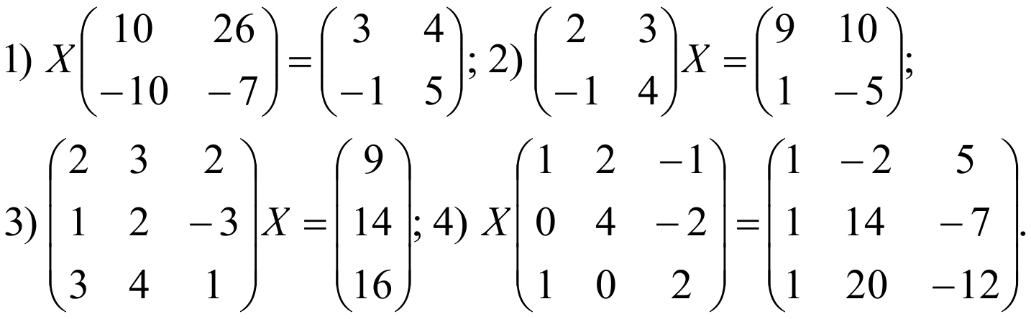  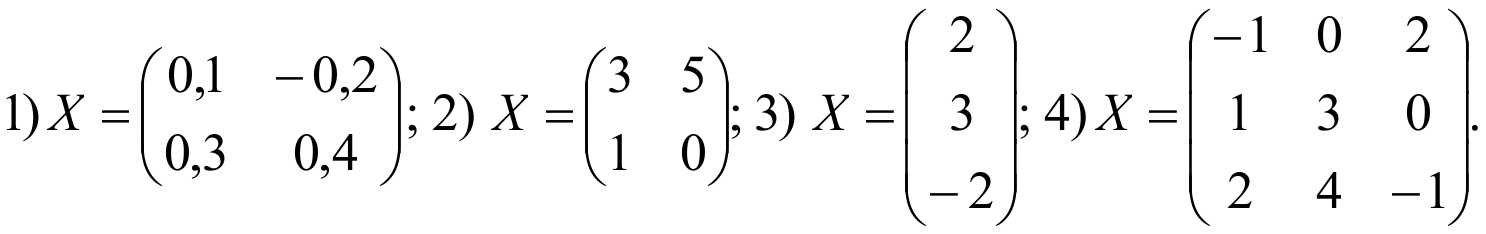 А = -6 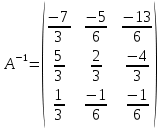 4) А = 8 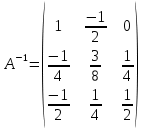 |
