тпэфм практические задания. ТПЭФМ_Практическое занятие 1_между лекциями 8 и 9. Занятие посвящено исследованию функций на экстремум и выпуклость и нахождение её асимптот
 Скачать 299 Kb. Скачать 299 Kb.
|
|
Практическое занятие посвящено исследованию функций на экстремум и выпуклость и нахождение её асимптот. Экстремум функции Если Необходимое условие экстремума функции Если Пусть Пример. Найти интервалы монотонности и экстремумы функции: 1. 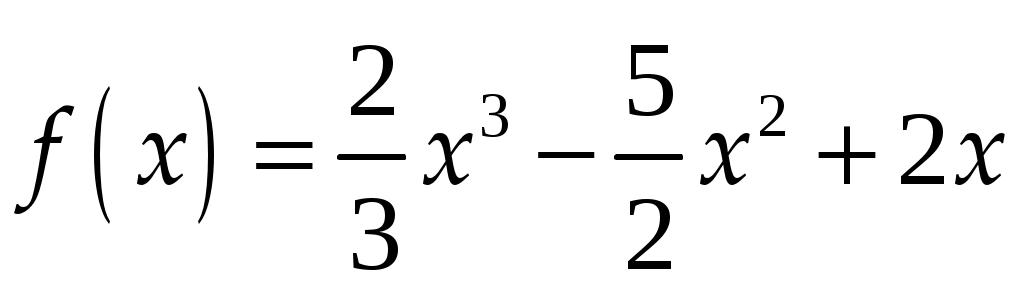 . .Решение. Первый способ. Функция определена на всей числовой оси, 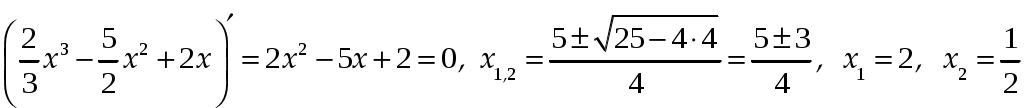 . . Для проверки знаков 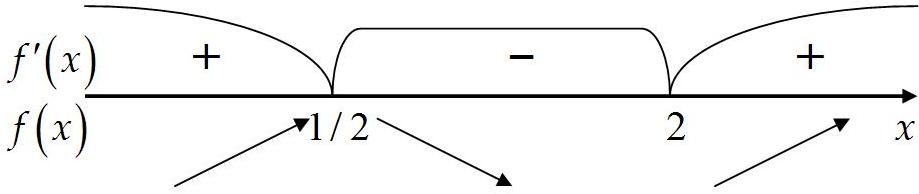 Функция возрастает на 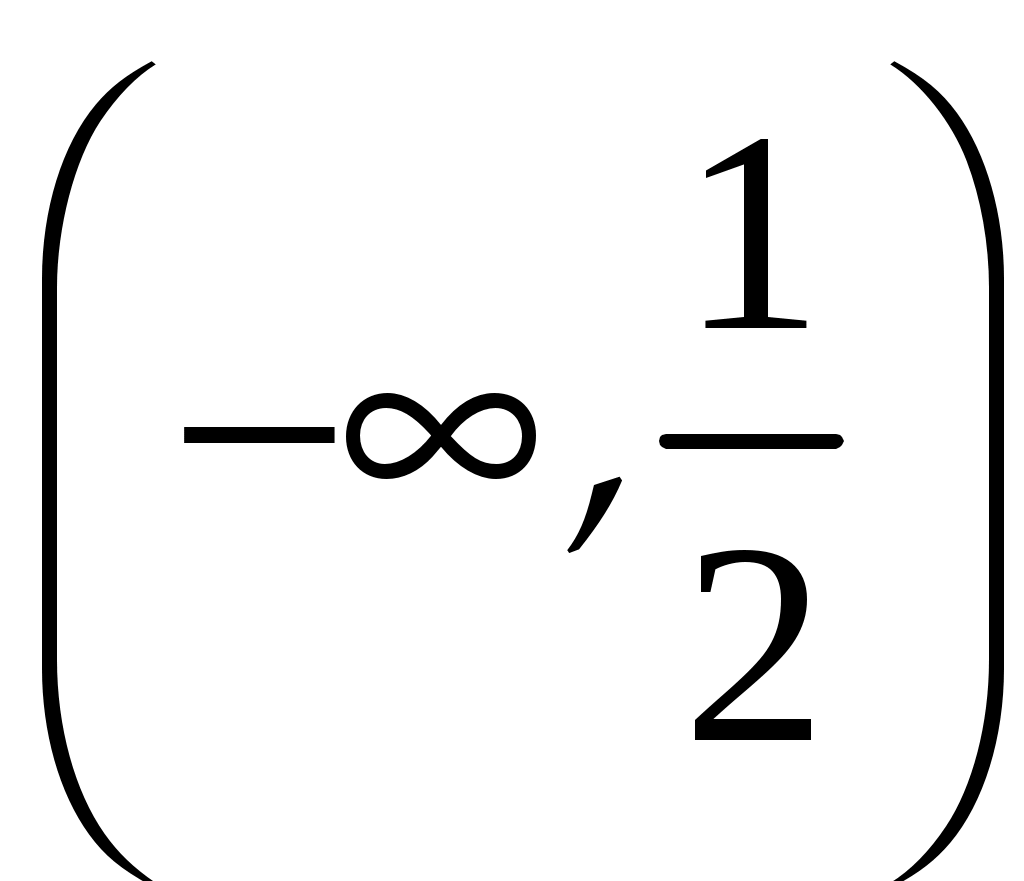 и и 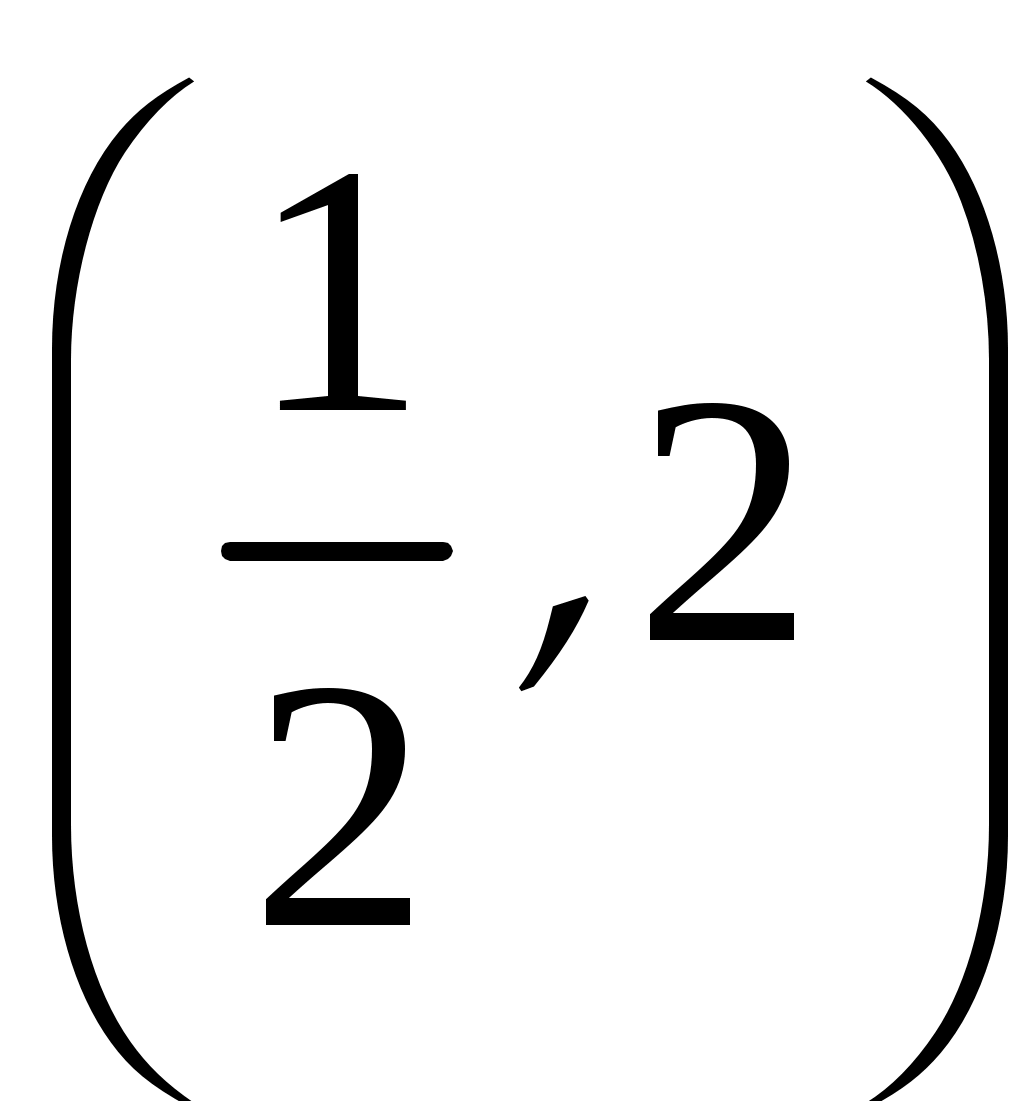 . . Точка максимума 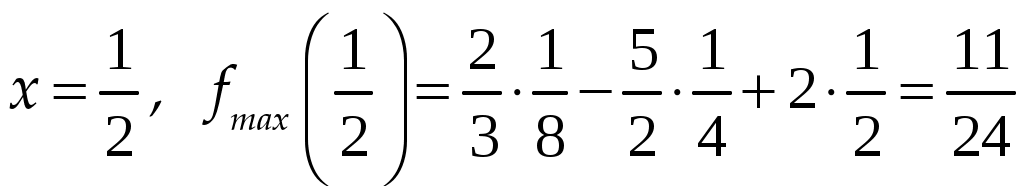 , , точка минимума 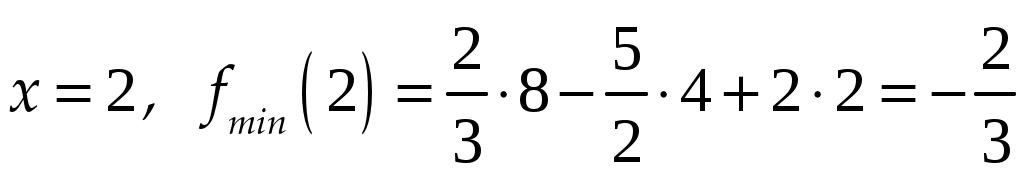 . .Учитывая, что 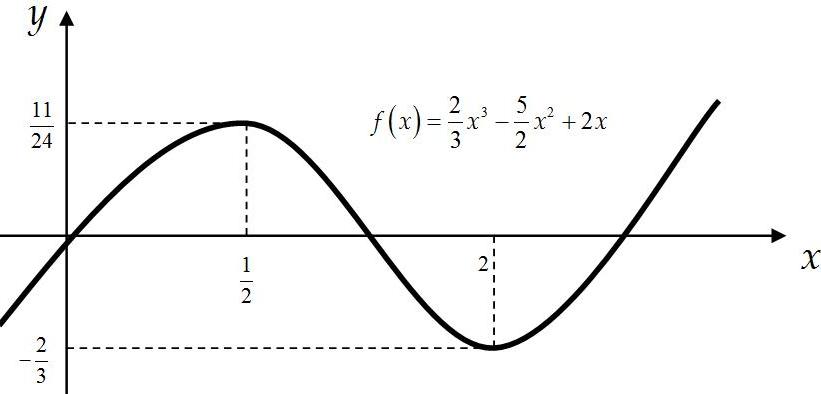 Второй способ: 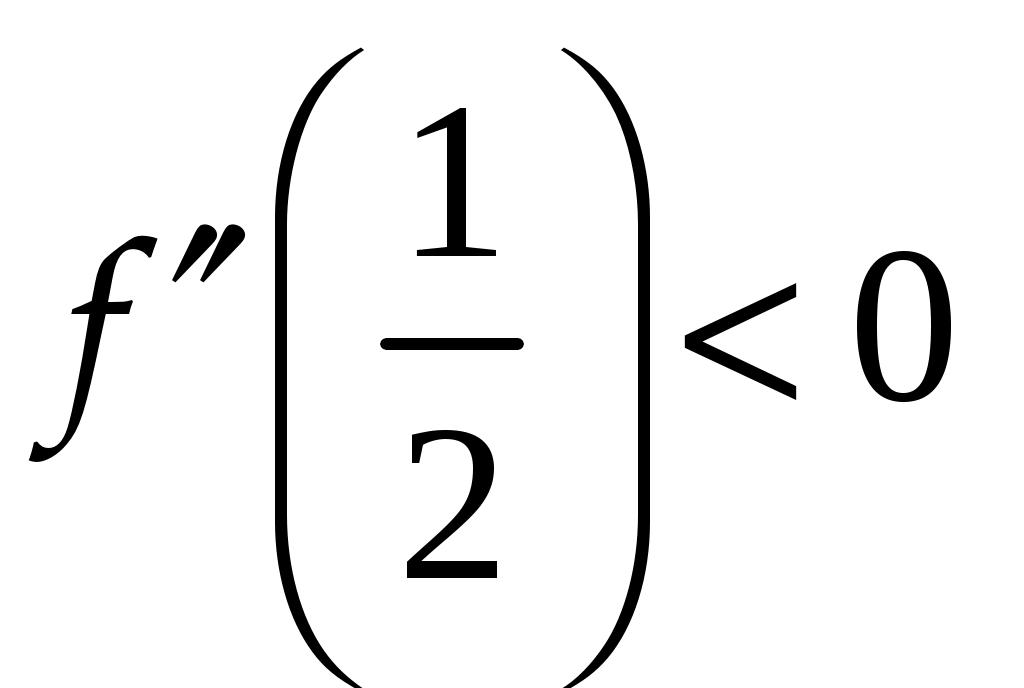 , значит при , значит приВыпуклость функции и точки перегиба Достаточные условия выпуклости функции Если Точкой перегибаназывается точка графика, разделяющая интервалы с разной выпуклостью. В окрестности этой точки кривая лежит по разные стороны от касательной, т.е. перегибается через касательную. Необходимое условие перегиба в точке Достаточное условие перегиба в точке Пример. Найти интервалы выпуклости и точки перегиба функции Решение. ООФ:  Точки перегиба: 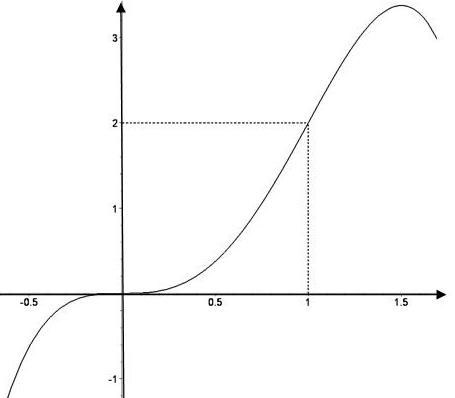 Асимптоты графика функции Асимптотой графика функции называют прямую, расстояние до которой от лежащей на кривой точки стремится к нулю при неограниченном удалении этой точки по кривой от начала координат. 1. Вертикальной асимптотой графика функции Вертикальные асимптоты функции следует искать в точках разрыва II рода (чаще всего это точки, где знаменатель функции равен нулю) или на концах области определения функции. Из вышесказанного следует очевидный факт: на интервале непрерывности функции вертикальные асимптоты отсутствуют. 2. Наклонной 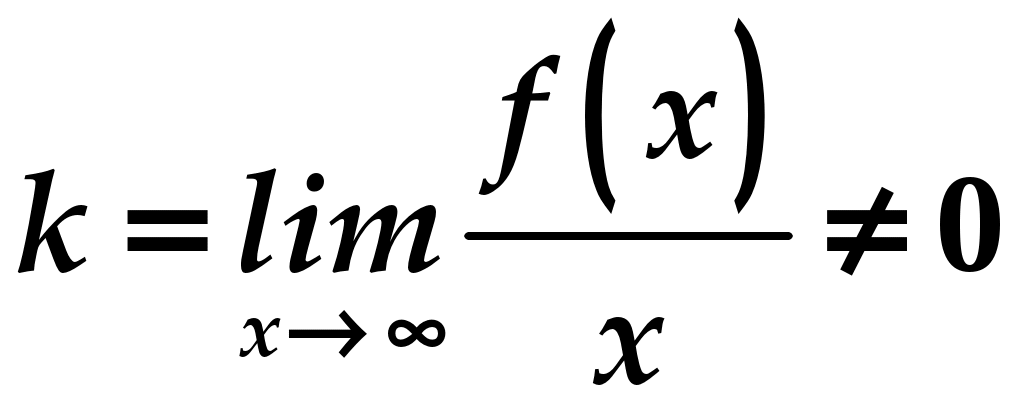 и В частном случае при Пример. Найти асимптоты графика функции 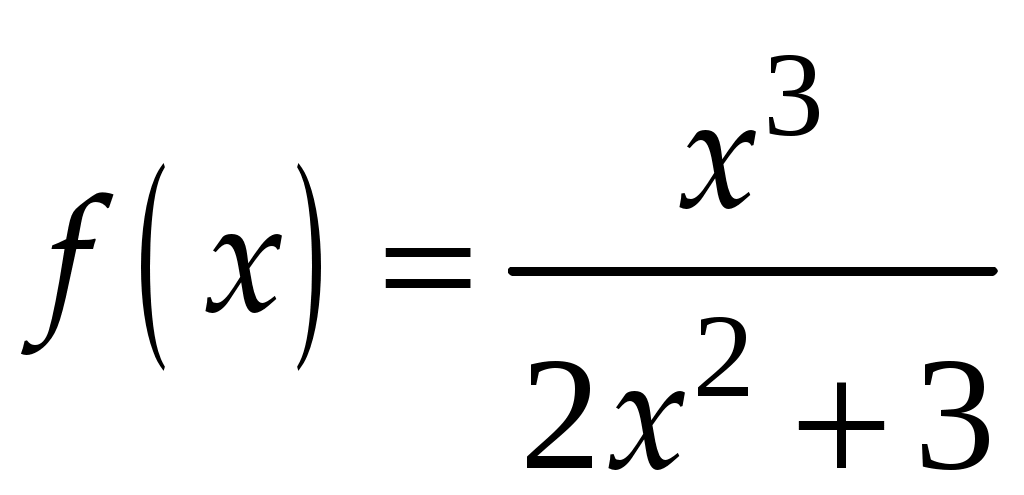 . .Решение. Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, вертикальные асимптоты отсутствуют. Проверим наличие наклонных асимптот: 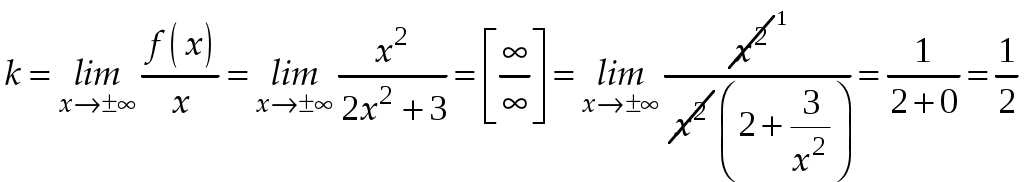 . . Первый предел конечен. В ходе вычисления второго предела для устранения неопределённости 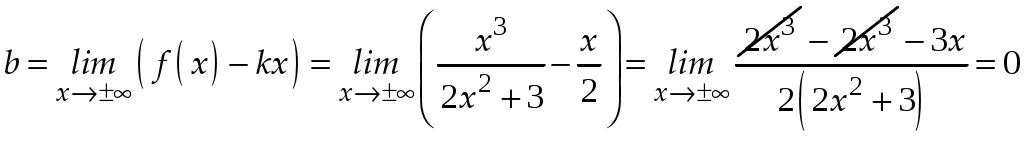 Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота 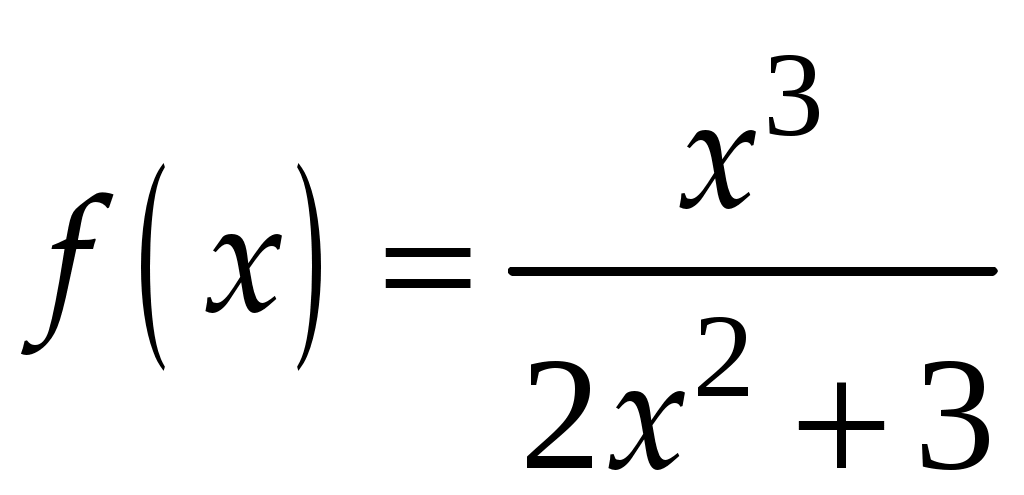 бесконечно близко приближается к прямой бесконечно близко приближается к прямой 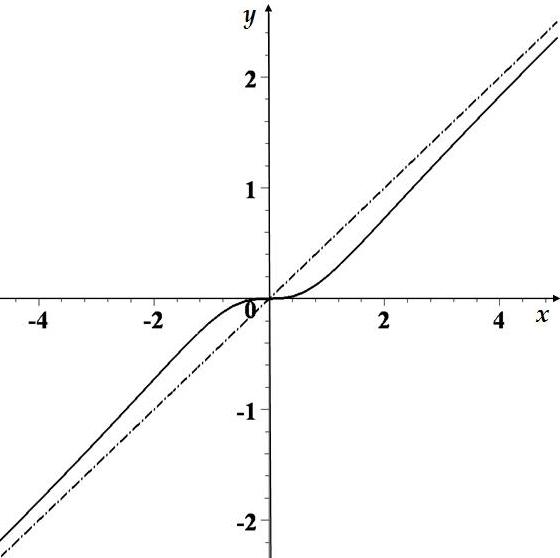 Он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности. |
