Курсова Інтерполяція. курсоваінтерполяція. 1. Аналіз теоретичної бази методів інтерполювання функції

• Название: 1. Аналіз теоретичної бази методів інтерполювання функції
• Анкор: Курсова Інтерполяція
• Дата: 28.06.2022
• Размер: 4.06 Mb.
• Имя файла: курсоваінтерполяція.rtf
• Тип: Документы; #618433
• страница: 1 из 3

Зміст
Анотація

Вступ

1. Аналіз теоретичної бази методів інтерполювання функції

2. Розробка алгоритмів та вибір оптимального алгоритму

3. Приклад програми інтерполювання функції за допомогою. Інтерполяційного многочлена Лагранжа

3.1 Інструкція користувача

.2 Лістинг програми

.3 Опис програми

.4 Тестування програми

Висновки

Перелік посилань
Анотація
Об’єктом дослідження є інтерполяційний многочлен Лагранжа для інтерполювання функцій. Розроблено оптимальний алгоритм та програму в середовищі системи C++ як за розміром пам'яті, необхідної для збереження даних, котрі обчислюються в ході виконаного алгоритму, так і за кількістю арифметичних операцій для обчислення за основною формулою. Програма має зручний та наочний інтерфейс, котрий максимально спрощує роботу з нею, та автоматичну перевірку коректності даних, що вводяться.
Вступ

Актуальність теми.

На практиці часто виникає задача відшукання функції за заданим значенням аргументу. Цю задачу вирішують методами інтерполяції функції. Є декілька прийомів розв’язку такої задачі, а саме: користуючись схемою Ейткіна, за допомого першої та другої формул Ньютона, а також за допомогою формул Гаусса, Стірлінга, Бесселя, але найпростішим є застосування інтерполяційної формули Лагранжа. Формула Лагранжа є досить зручна і використовується не лише у випадку рівновіддалених вузлів, але й у випадку вузлів інтерполяції, заданих довільно, що дає можливість широкого її застосування у порівняні з іншими формулами інтерполювання.

Мета дослідження.

Метою роботи є дослідження можливості використання інтерполяційного многочлена Лагранжа для інтерполювання функцій.

Задача дослідження:

· проаналізувати існуючі методи інтерполювання функції та обґрунтувати переваги використання інтерполяційного многочлена Лагранжа по відношенню до існуючих;

· розробити алгоритм інтерполювання функції та здійснити вибір найоптимальнішого з них;

· розробити програму інтерполюванням функції з використанням інтерполяційного многочлена Лагранжа та провести її тестування.

Об’єкт дослідження. Об’єктом дослідження є многочлен Лагранжа для інтерполювання функції.

Структура курсової роботи.

Курсова робота складається з трьох основних розділів. В першому розділі наведено аналіз теоретичної бази методів інтерполювання функції та приклад застосування за формулою Лагранжа. У другому розділі розроблено оптимальний алгоритм за критерієм комплексної ефективності, що враховує затрати часу та пам'яті для його виконання, за даним методом. Третій розділ містить інструкцію користувача, лістинг програми, опис програми та результати тестування.

інтерполювання функція алгоритм многочлен
1. Аналіз теоретичної бази методів інтерполювання функції
В обчислювальній практиці часто доводиться мати справу з функціями , заданими таблицями їхніх значень для деяких скінченних множин значень .

У процесі розв’язування задачі необхідно використовувати значення для проміжних значень аргументу. У цьому випадку будують функцію , досить просту для обчислень, що у заданих точках приймає значення , а в інших точках відрізка , що належить області визначення , приблизно є функцією з тим або іншим степенем точності, і при розв’язуванні задачі замість функції оперують із функцією . Задача побудови такої функції називається задачею інтерполяції. Найчастіше інтерполюючи функцію відшукують у вигляді алгебраїчного многочлена. Такий спосіб наближення має у своїй основі гіпотезу, що на невеликих відрізках зміни х функція може бути досить добре наближена за допомогою параболи деякого порядку, аналітичним виразом якої й буде алгебраїчний многочлен.

Інтерполяцію доводиться інколи застосовувати і в тому випадку, коли для функції відомо й аналітичне значення, за допомогою якого можна обчислювати її значення для будь-якого значення з відрізка в якому вона визначена, але обчислення кожного значення сполучено з великим об'ємом обчислень. Якщо в процесі розв’язування задачі необхідно знаходити значення функції для дуже великої кількості значень аргументу, то прямий спосіб вимагав би величезної обчислювальної роботи. У цьому випадку для зменшення об'єму обчислень прибігають до інтерполяції, тобто обчислюють кілька значень де і по них будують просту інтерполяційну функцію , за допомогою якої й обчислюють наближені значення в інших точках [1-2].

Нехай на відрізку визначено певний клас функцій , наприклад клас алгебраїчних многочленів, а в точках цього проміжку задано значення деякої функції . Наближену заміну функції на відрізку однією з функцій цього класу так, щоб функція в точках набувала тих самих значень, що й функція , тобто щоб , називають інтерполюванням, або інтерполяцією. Точки називають вузлами інтерполювання, функцію - інтерполюючою функцією, а формулу , за допомогою якої обчислюють значення функції у проміжку , - інтерполяційною формулою [3].

З геометричного погляду задача інтерполювання полягає в знаходженні кривої певного класу (рис. 1) , яка проходить через точки площини з координатами .


Рисунок 1 - Геометрична інтерпретація інтерполювання функції

=P_n(x)

y=F(x)

0 a=x₀ x₁ x₂x_k x_k+1 b=x_n
Якщо функція належить класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.

У деяких випадках доцільніше використовувати інші класи інтерполюючих функцій. Якщо, наприклад, функція періодична, то функцію природно вибирати з класу тригонометричних многочленів, а якщо функція перетворюється в нескінченність у заданих точках або поблизу них, то функцію доцільно вибирати з класу раціональних функцій.

Розглядатимемо лише задачу параболічного інтерполювання, яку сформулюємо так: в різних точках задано значення функції і треба побудувати многочлен
, (1)
степеня , який задовольняв би умови
, (2)
Для визначення коефіцієнтів многочлена (1), який задовольняє умови (2), запишемо систему -го лінійних рівнянь вигляду [4]:

Ця система має єдиний розв'язок, бо її визначник є визначником Вандермонда, який не дорівнює нулю, бо вузли різні. А тому й задача параболічного інтерполювання має єдиний розв'язок, тобто існує єдиний алгебраїчний многочлен виду (1.1), що задовольняє умови (2). Многочлен , який задовольняє умови (2), називають інтерполяційним многочленом, наближену рівність - інтерполяційною формулою, а різницю - залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен, що задовольняє умови (2), і єдиний, проте можливі різні форми його запису.

Інтерполяційний многочлен будують тоді, коли:

1) функцію задано табличну для деяких значень аргументу, а треба знайти її значення для значень аргументу, яких у таблиці немає;

2) функцію задано графічно, наприклад за допомогою самописного приладу, а треба знайти її наближений аналітичний вираз;

3) функцію задано аналітично, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо) [5].

Тоді залежно від вибору критерію згоди й, зокрема, від кількості, точок узгодження і (будемо називати їхніми вузлами), тобто точок, у яких відома інформація про і, можливо, її похідних, можна розглянути різні конкретні способи інтерполяції. А саме, у даному розділі буде досить докладно розглядатися класична Лагранжеві інтерполяція, що служить основою багатьох чисельних методів, зокрема, наближеного диференціювання і інтегрування. Також отримаємо знання про інтерполяційну схему Ейткіна, окремими випадками якого є, з одного боку, многочлен Тейлора (при ), з іншого боку - многочлен Лагранжа (при ) [2].

Нехай у точках якщо задано значення функції . Треба побудувати многочлен степеня п, який у вузлах набуває тих самих значень, що й функція , тобто
. (3)
Шукатимемо інтерполяційний многочлен у такому вигляді:

(4) де коефіцієнти невідомі. Кожний доданок виразу (4) є многочленом степеня , причому при кожному з коефіцієнтів множника немає.

Визначимо коефіцієнти , використавши умову (3). Поклавши в (4) , дістанемо
звідки



Якщо в (4) покласти , то

а отже

Аналогічно обчислюємо

Підставивши ці значення коефіцієнтів в (4), дістанемо вираз інтерполяційного многочлена
(5)
Многочлен виду (5) називають інтерполяційним многочленом Лагранжа, а наближену рівність
(6)
- інтерполяційною формулою Лагранжа.

Інтерполяційний многочлен Лагранжа можна записати компактніше. Для цього введемо многочлен -го степеня вигляду
(7)

Продиференціювавши по цей добуток, дістанемо:

Поклавши тут , матимемо
(8)
Підставивши (7) і (8) в (5), знайдемо
(9)
Вирази , , що є коефіцієнтами при у многочлені Лагранжа, називають коефіцієнтами Лагранжа.

Оцінка похибки інтерполяційної формули Лагранжа. Якщо функція на відрізку є многочленом степеня, що менший або дорівнює , то з єдності інтерполяційного многочлена випливає, що інтерполяційний многочлен тотожно дорівнює , тобто ,

Якщо на відрізку , який містить вузли інтерполяції , не є многочленом степеня, що менший або дорівнює , то різниця (10) дорівнюватиме нулю лише у вузлах інтерполяції де, , а в інших точках відрізка вона відмінна від тотожного нуля. Функцію яка характеризує точність наближення функції інтерполяційним многочленом , називають залишковим членом інтерполяційної формули Лагранжа (6), або по-хибкою інтерполювання. Якщо відомий аналітичний вираз функції , то можна оцінити

Справедлива така теорема.

Теорема. Якщо вузли інтерполювання різні і належать відрізку , а функція диференційована раз на відрізку , то для будь-якої точки існує така точка , що для похибки інтерполювання справедлива рівність
(11)

де [5-14].
Для кожного нового значення аргументу х або при підвищенні порядку многочлена (а це веде до залучення нових вузлів) всі обчислення виконують заново. А це значно збільшує обсяг обчислювальної роботи. Значно спростити і зменшити її можна тоді, коли скористатись інтерполяційною схемою Ейткіна. У цій схемі в процесі обчислення поступово залучаються все нові й нові вузли доти, поки самі обчислення не покажуть, що необхідної точності досягнуто [5].

Якщо в ( )-му вузлах інтерполювання функція набуває значень , то значення інтерполяційного многочлена степеня п в точці , що не збігається з вузлами інтерполювання, можна обчислити за формулою


де і - значення інтерполяційних многочленів ( )-го степеня, обчислених у точці х на попередньому кроці обчислень. Легко впевнитись, що і збігається з інтерполяційним многочленом Лагранжа -го степеня (таблиця 1).
Таблиця 1

Різниця

0

…

1

…

…

…

…

…

…

…

…

…

…

…

…

…

Отже, щоб обчислити в точці х значення інтерполяційного многочлена -го степеня за схемою Ейткіна, треба в цій точці обчислити значення лінійних, -1 квадратичних, -2 кубічних многочленів і так далі, два многочлени ( -і)-го степеня і, нарешті, один многочлен -го степеня. Всі ці многочлени виражають через визначник 2-го порядку, а це робить обчислення однотипними, циклічними [2,5,10].

Часто інтерполювання ведеться для функцій, заданих таблицями з рівновіддаленими значеннями аргументу (тобто такими, що будь-який (вузол інтерполяції) можна подати у вигляді а - деяка постійна величина, яка називається кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а також проведення обчислень по ним значно спрощується.

Для побудови формули Ньютона необхідно ввести поняття кінцевих різниць.

Кінцевими різницями називають різниці між значеннями функції в сусідніх вузлах (точках 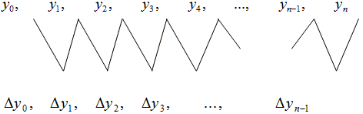) інтерполяції:

де , Отримані кінцеві різниці будемо називати кінцевими різницями першого порядку. Кінцевою різницею першого порядку називається різність між значеннями функції в сусідніх вузлах інтерполяції. В загальному вигляді кінцеву різницю першого порядку можна записати як .

Якщо функція, що досліджується, задана значеннями в рівновіддалених вузлах інтерполяції, тобто , то для побудови її аналітичної залежності зручно використовувати першу інтерполяційну формулу Ньютона.

Перша інтерполяційна формулу Ньютона (12).
(12)
На практиці часто використовують формулу Ньютона в іншому вигляді. Для цього введемо заміну , де h - крок інтерполяції, а q - число кроків. Тоді перша інтерполяційна формула Ньютона прийме вигляд (13):
(13)
Формулу (13) зручно використати для інтерполювання на початку відрізку інтерполяції [a; b] , де q мале за абсолютною величиною.

Якщо за число вузлів інтерполяції прийняти n-1, то отримаємо формулу лінійного інтерполювання

При n=2 отримаємо формулу параболічного, або квадратичного інтерполювання

На практиці часто буває необхідно зменшити крок інтерполяції будь-якої таблиці з рівновіддаленими аргументами. В таблиці можна вважати, що кількість вузлів інтерполяції необмежена. Тоді вибирають n так, щоб кінцева різниця була постійна з заданим ступенем точності. За початкове значення можна вибирати будь-яке значення аргументу.

Часто користуються формулами центральних різниць, до яких відносяться формули Гаусcа, Бесселя, Стірлінга.

Інтерполяційна формула Гаусса - формула, яка використовує в якості вузлів інтерполяції найближчі до точки інтерполяції x вузли. Якщо формула написана за вузлами , то вона зветься формулою Гаусса для інтерполяції вперед (14),
(14)
А формула написана за вузлами зветься формулою Гаусса для інтерполяції назад (15).
(15)
В формулах (14) і (15) використані кінцеві різниці, які визначаються в такий спосіб [5]:
.
Перевага інтерполяційної формули Гаусса полягає в тому, що зазначений вибір вузлів інтерполяції забезпечує найкращу оцінку залишкового члена в порівнянні з будь-яким іншим вибором, а впорядкованість вузлів у міру їх близькості до точки інтерполяції зменшує обчислювальну похибку інтерполяції.

Часто використовується інтерполяційна формула Бесселя, яка служить для знаходження значення функції у міжвузловій точці. Для виведення цієї формули скористаємось другою інтерполяційною формулою Гаусса (14):
(16)
у скороченому вигляді (17):
(17)

де .
Інтерполяційна формула Бесселя застосовується при інтерполяції функцій для значень х , близьких середині а між двома вузлами, тут природно брати парне число вузлів х _{- до} ..., х _-1 , x ₀ , x ₁ ..., x _до , x _{до + 1} , і розташовувати їх симетрично відносно а (x ₀ < а < x ₁ ).

Взявши середнє арифметичне першої та другої інтерполяційних формул Гаусса, отримаємо формулу Стірлінга:
де .
Легко побачити, що при

Формула Стірлінга використовується для інтерполювання в середині таблиці при значеннях q, близьких до нуля. Практично її використовують при │q│≤ 0,25 [12,13,14].