Курсова Інтерполяція. курсоваінтерполяція. 1. Аналіз теоретичної бази методів інтерполювання функції
 Скачать 4.06 Mb.
|
|
Приклад розв’язування задачі: Побудувати інтерполяційний многочлен Лагранжа одинадцятого степеня для функції  , заданої аналітично:  за такими даними: кроком  , на проміжку  та знайти значення функції у точці  використовуючи формулу (5), розв’язок подано в табл. 2.Розв’язання. , , .Таблиця 2
Знайдемо інтерполяційний многочлен Лагранжа.   Побудувавши інтерполяційний многочлен Лагранжа, перевіримо вірність многочлена. Для цього підставимо значення  аргументу у вираз. Перевіримо вірність результату, для цього скористаємося схемою Горнера.   2. Розробка алгоритмів та вибір оптимального алгоритму При розробці алгоритму обчислення значення функції, яке відповідає заданому значенню аргументу, будемо використовувати формулу (5), що наведена в розділі 1. Аналіз формули (5) та прикладу наведеного в першому розділі показує, що для обчислення значення аргументу необхідно 16 операцій додавання, 204 операцій віднімання, 236 операцій множення та 10 операцій ділення. З врахуванням того, що час виконання операцій множення та ділення відповідно в 1,14 та 2,33 рази більший за час виконання операцій додавання (віднімання) при використанні арифметичного співпроцесора, загальна кількість операцій обчислення значення функції використовуючи многочлен Лагранжа складає  Алгоритм можна побудувати таким чином, щоб спочатку перевірити умову, чи не збігається значення аргументу  з будь-яким із вузлів   . Якщо ця умова не підтвердилась, то проводяться відповідні обчислення, що передбачені у блоках 7-12. В цьому випадку для збереження значень аргументу та функції необхідно 2 комірки пам’яті. Блок-схема першого алгоритму подана на рис. 2.1.Інший спосіб побудови алгоритму полягає в тому, що для знаходження значення аргументу застосована схема Ейткіна (рис. 2.2). Аналіз формули показує, що для обчислення значення аргументу необхідно 264 операцій віднімання, 198 операцій множення та 66 операцій ділення  В даному випадку для збереження результатів обчислення необхідно також 2 комірки пам’яті. Комплексний коефіцієнт ефективності  одного алгоритму в порівнянні з іншим можна обчислити за формулою: ,де  - коефіцієнт ефективності за часом виконання алгоритму; - коефіцієнт ефективності за затратами пам’яті алгоритму.Оскільки коефіцієнт ефективності за часом виконання алгоритму можна приблизно оцінити за кількістю арифметичних операцій алгоритму, то комплексний коефіцієнт ефективності описаних вище алгоритмів складає  Подальші обчислення будуть проводитися мовою програмування С++, яка дасть можливість знаходити значення аргументу, яке відповідає заданому значенню функції, якого в табл. 2 немає. 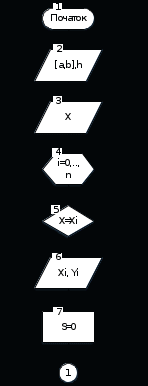 Рисунок 2.1 - Блок-схема першого алгоритму обчислення значення функції з використанням інтерполяційного многочлена Лагранжа 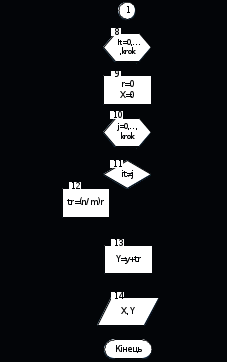 Рисунок 2.1 - Продовження  Рисунок 2.2 - Блок-схема другого алгоритму обчислення значення функції за схемою Ейткіна 3. Приклад програми інтерполювання функції за допомогою інтерполяційного многочленна Лагранжа 3.1 Інструкція користувача Після виклику C++ із середовища Windows на екрані з'являється командне вікно середовища C++. Це вікно є основним у C++. У ньому відображаються символи команд, що набираються користувачем на клавіатурі, результати виконання цих команд, текст програми, що виконується, а також інформація про помилки виконання програми, яка розпізнана системою. Ознакою того, що програма C++ готова до сприйняття і виконання чергової команди, є наявність в останньому рядку текстового поля вікна миготливої вертикальної риски. У верхній частині командного вікна (безпосередньо під заголовком C++) розташований рядок меню, що складається з 11 меню - Файл, Правка, Пошук, Вигляд, Проект, Виконати, Налаштування, Сервіс, CVS, Вікно, Довідка. Під головним меню розміщена панель інструментів з піктограмами, що дозволяють виконувати деякі найбільше часто використовувані операції. 1. Відкриття меню здійснюється натисненням миші. Щоб вибрати будь-яку команду меню, досить установити курсор на імені команди і натиснути ліву кнопку миші. 2. Текст програми міститься в одному файлі: файл основної програми з іменем Kyrsova. Для відкриття його необхідно вибрати у меню Файл команду Відкрити, що відкриває діалогове вікно з переліком файлів поточної папки. . Вибір необхідного файлу з цього списку і наступне натискання кнопки OK приводить до появи вікна Редактора/Налагодження, який дає змогу не тільки коректувати програму, але і проводити її відладку. Запуск програми здійснюється вибором в меню Виконати команди виконати, або натисненням клавіші F9. . В результаті запуску програми з’явиться командне вікно, в якому необхідно ввести значення проміжку  , крок  та значення аргументу  . По завершенні введення значень в командному вікні буде зазначено значення функції .3.2 Лістинг програми #include #include #include #include .02778,0.01852,0.01316,0.009804, .007576,0.006024,0.004902,0.004065}; x[11]={1,2,3,4,5,6,7,8,9,10,11};L(float xp,int n,int i) {Chesl; float Znam;=1; Znam=1; int k;(k=0; k!=n; k++) {(k==i) continue;*=xp-x[k]; //Обчислення чисельника многочлена Лагранжа }(k=0; k!=n; k++) {(x[i]==x[k]) continue; *=x[i]-x[k]; // Обчислення знаменника многочлена Лагранжа }Chesl/Znam; }main() { ("chcp 1251");("cls");n,a,b;float px; <<"Введіть проміжок:"< } 3.3 Опис програми В даному файлі описані всі змінні та присвоєні їм певні значення, необхідні для обчислення інтерполювання з використанням інтерполяційного многочленна Лагранжа, а також власний процес обчислення методу. З метою ефективного використання пам’яті для збереження початкових значень системи, вони зберігаються в динамічній пам’яті, що дозволяє відводити під них місце динамічного розміру в залежності від кількості заданих даних. Файл Kyrsova-Lagranzh.PAS. містить описи структури методу та функцій, що використовуються основною програмою, та описи внутрішніх операторів. Нижче наведено список загальних операторів, їх призначення та основні властивості. Команда int описує цілий тип змінних. Команда float описує дійсний тип змінних. Команда cout призначена для виведення значень на екран і має такий загальний вигляд: cout < список >. Команда cin призначена для введення даних і має такий загальний вигляд: cin (< список змінних >). Оператор циклу for призначений для повторного виконання операцій, число яких заздалегідь відоме. Оператор циклу for ще називають оператор циклу з параметром. Загальний вигляд оператор циклу for: for (< початок масиву>кінець масиву < крок проходу по масиву >). Оператор умови if використовується для виразів результат яких має стандартний булевский тип. Неповне розгалуження реалізується за допомогою оператора if і має такий загальний вигляд: if < логічний вираз { < команда >}. Оператор continue призначений до поверненння дії назад і має такий загальний вигляд: <умова> continue. Команда getch зупиняє роботу програми. |
