ТОЭ_решение. 1. Определение напряжения холостого хода с помощью второго закона Кирхгофа
 Скачать 1.05 Mb.
|
|
Билет №5 1. Определение напряжения холостого хода с помощью второго закона Кирхгофа. В соответствии с принципом наложения (суперпозиции) напряжение холостого хода может быть найдено как сумма напряжений от действия каждой ЭДС в отдельности:  ,где  – напряжение холостого хода, создаваемое ЭДС  (рис. 6.4, а);  – напряжениехолостого хода от действия ЭДС  (рис. 6.4, б).Знаки в правой части последнего уравнения определяются взаимными направлениями стрелок  , и (рис. 6.2. и 6.4). Как следует направлять , мы только что выяснили. Напряжения и рекомендуется направлять в ту же сторону, хотя это необязательно. Если мы решили направить и в разные стороны, то будет равно их разности.Токи от действия каждой ЭДС в отдельности, называемые частичными токами, на схемах рис. 6.4, а и 6.4, б направляются уже не произвольно, а в соответствии с действующей в цепи единственной ЭДС – по её стрелке. Для облегчения понимания структуры цепи рекомендуется представить ее в более удобном виде. Схему рис. 6.4, а, например, можно изобразить так, как показано на рис. 6.5. 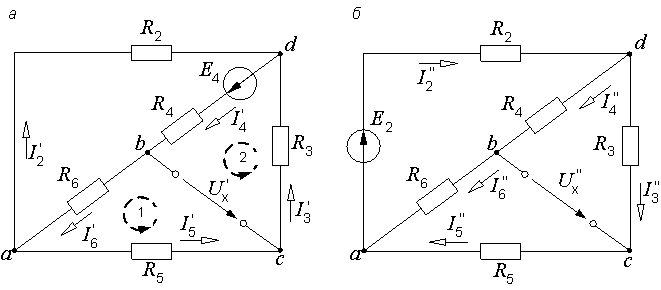 Рис. 6.4. Схемы для расчета напряжения холостого хода 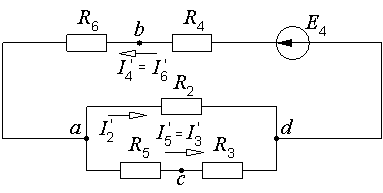 Рис. 6.5. Упрощенная схема Порядок расчета схемы рис. 6.5 следующий. Определяем общее сопротивление цепи относительно зажимов источника:  .Находим ток, протекающий по ветви с ЭДС:  .Рассчитываем напряжение  на зажимах параллельно соединенных ветвей: .И наконец, находим токи в параллельных ветвях: 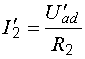 ;  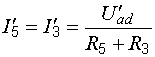.Последние два тока можно рассчитать, и не находя напряжения  .Рассмотрим часть электрической цепи, состоящей из двух параллельно соединенных сопротивлений (рис.6.6). Требуется по известному току 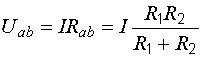 найти токи  и  . Сначала определяем напряжение на участке ab: .Затем по закону Ома находим токи:  ;  .Полученные формулы дают следующее простое правило. Ток в одной из параллельных ветвей равен произведению общего тока и сопротивления соседней ветви, деленному на сумму сопротивлений параллельных ветвей. 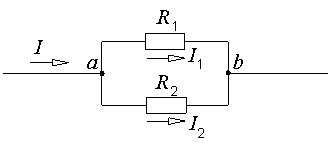 Рис.6.6. Определение токов в параллельных ветвях В соответствии с этим правилом для схемы рис. 6.5 имеем: 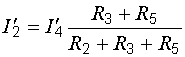 ;  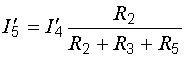.Напряжение  находим по схеме рис. 6.4, а из уравнения, составленного по второму закону Кирхгофа для контура, включающего в себя это напряжение. Например, контур, отмеченный дугообразной пунктирной стрелкой 1, состоит из двух ветвей (шестой и пятой) и стрелки . ЭДС в этом контуре нет, поэтому в соответствии со вторым законом Кирхгофа .Отсюда  .Можно воспользоваться и контуром 2. Для него  ,откуда  .Схема рис. 6.4, б рассчитывается аналогично: 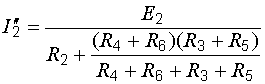 ;  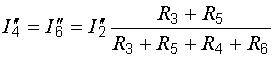; ; или  .Если в результате расчета ЭДС  окажется отрицательной, то во все формулы ее значение следует подставлять со знаком минус, не меняя, конечно, самих формул и схем.2. Метод узловых потенциалов. В методе узловых напряжений независимыми переменными являются напряжения узлов цепи относительно выбранного базисного (опорного) узла. Эти величины называют узловыми напряжениями. Положительные направления узловых напряжений указывают стрелками от рассматриваемых узлов к базисному. В качестве последнего удобно выбирать заземленный узел или узел, в котором сходится наибольшее число ветвей. Уравнения составляют только на основе первого закона Кирхгофа. Если принять потенциал базисного узла равным нулю, то узловые напряжения будут равны потенциалам соответствующих узлов. Поэтому метод называют также методом узловых потенциалов. Составление уравнений по методу узловых напряжений рассмотрим на примере. На рисунке изображена цепь, имеющая четыре узла. Примем узел 0 за базисный. Запишем уравнения по первому закону Кирхгофа для всех узлов, кроме базисного.  Узел 1: I1 + I2 = J1 Узел 2: I3 – I2 + I4 = - J1 Узел 2: I5 – I4 = - J5 + J4 Обозначим напряжения узлов V1, V2 и V3. Выразим токи ветвей через узловые напряжения и проводимости ветвей: I1 = G1V1; I2 = G2(V1 – V2); I3 = G3V2; I4 = G4(V2 – V3); I5 = G5V3 Подставим полученные равенства в уравнения. После простых преобразований получим (G1 + G2)V1 – G2V2 = J1 - G2V1 + (G2+ G3 + G4)V2 – G4V3 = - J4 - G4V2 + (G5 + G4)V3 = - J4 – J5 Полученная система уравнений позволяет легко найти искомые узловые напряжения. Ее называют системой узловых уравнений. В общем случае, если цепь имеет nу узлов, нам необходимо составить nу - 1 узловых уравнений. Узловые уравнения записаны на основе уравнений по первому закону Кирхгофа. Поэтому анализируемая цепь может содержать только независимые источники тока. Если в схеме имеются источники напряжения, они должны быть заменены эквивалентными источниками тока. Узловые уравнения удобно записывать в матричной форме. В общем виде для цепи, имеющей n + 1 узел, эти уравнения имеют вид 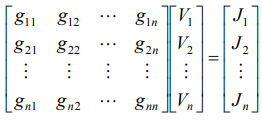 Элементы на главной диагонали матрицы узловых проводимостей называют собственными проводимостями узлов. Собственная проводимость i -го узла ii g равна сумме проводимостей ветвей, сходящихся в этом узле. Элементы матрицы [G], расположенные вне главной диагонали, называют взаимными проводимостями. Взаимная проводимость между узлами i и j gij равна проводимости ветви, соединяющей эти узлы, взятой со знаком минус. В пассивной цепи, которая не содержит управляемых источников и идеальных ОУ, gij = gji , и матрица узловых проводимостей симметрична относительно главной диагонали. Элементы вектора узловых токов равны алгебраической сумме токов источников, сходящихся в соответствующем узле. 3. Задача. Дано: R1 = 8 Ом, R2 = 15 Ом, R3 = 16 Ом, R4 = 12 Ом, R5 = 21 Ом, R6 = 8 Ом, E2 = 12 В, E3 = 26 В. Найти: Напряжение на резисторе R1. 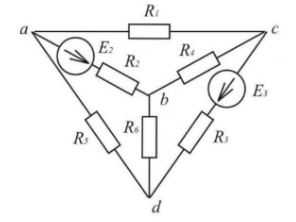 Сделаем отдельный рисунок, на котором укажем направление токов в ветвях и контурных токов. И уже относительно этого рисунка будем вести дальнейшие расчёты: 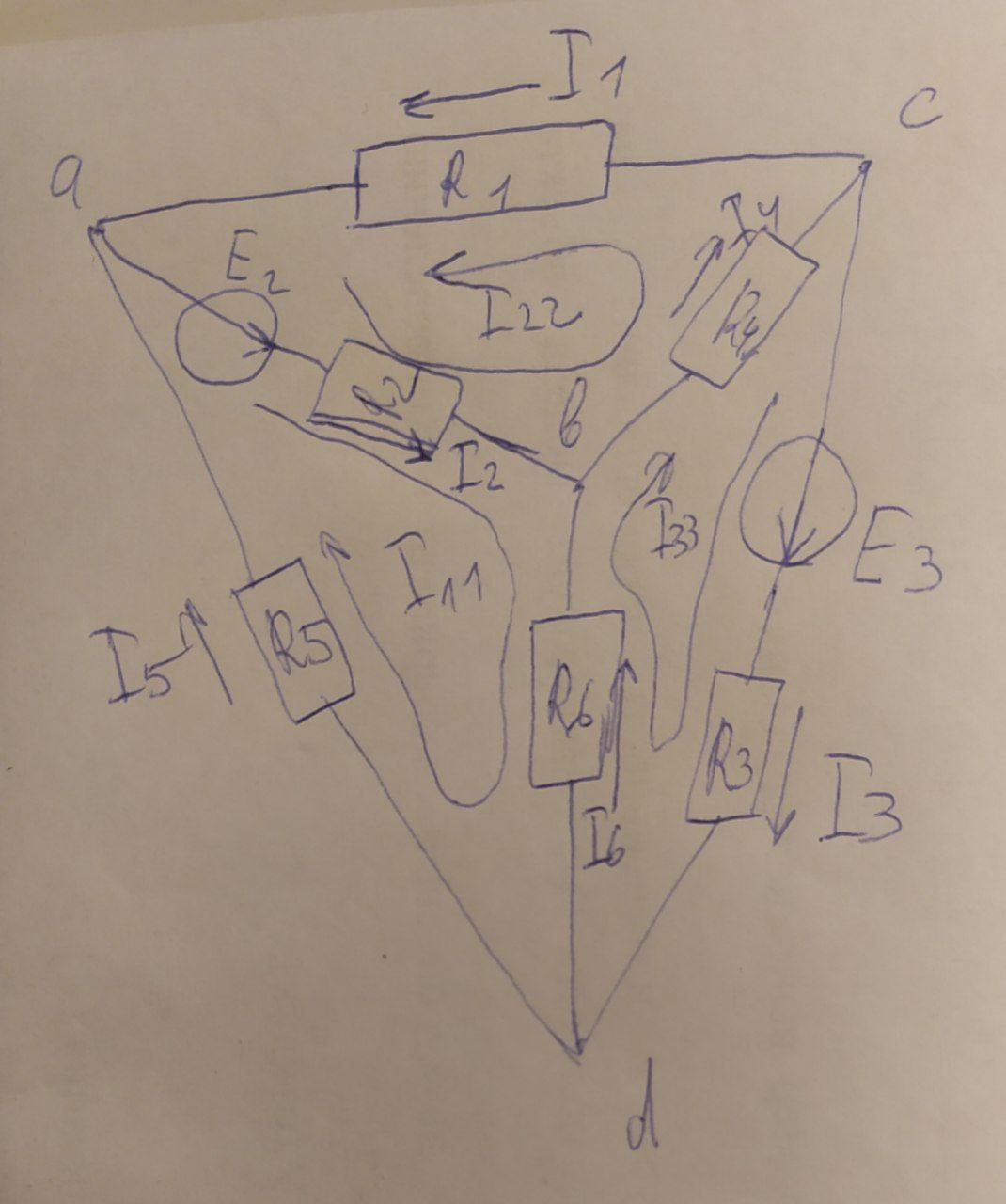 Составим уравнения по методу контурных токов: E2 = I22(r1 + r2 + r4) + I33r4 + I11r2 E2 = I11(r6 + r2 + r5) - I33r6 + I22r2 E3 = I33 (r6 + r3 + r4) - I11r6 + I22r4 Подставим числа: 12 = 35I22 + 12I33 + 15I11 12 = 44I11 - 8I33 + 15I22 26 = 36I33 - 8I11 + 12I22 Получим следующее решение: I11 = 0,4938 А; I33 = 0,8899 А; I22 = -0,1739 А I1 = I22, поэтому U11 = r1I1 = r1I22 = 1,3912 В |