Теоретическая механика. 2. Исследование условий равновесия данной системы сил

• Название: 2. Исследование условий равновесия данной системы сил
• Дата: 07.05.2023
• Размер: 280.67 Kb.
• Имя файла: Теоретическая механика.docx
• Тип: Исследование; #1113908

1.СТАТИКА

 

1.1.Основные понятия и определения

 

Основным объектом исследования статики является сила. Сила - это количественная мера  взаимодействия  материальных  тел. В самом деле, проявление  любой  силы  вызывается взаимодействием тел, например, сила тяжести вызывается притяжением данного  тела к Земле, сила упругости - взаимодействием тела и пружины, прикрепленной к нему. Действие  силы  определяется  тремя  факторами: величиной (модулем), направлением   и  точкой  приложения, то есть сила является векторной величиной и изображается  в  виде отрезка, на конце  которого ставится стрелка (рис.1.2).

Величина силы в масштабе равна длине отрезка. В тексте вектор силы обозначается буквой со стрелкой наверху  -  , а модуль силы - теми же буквами, но без стрелки, либо обозначением вектора силы, заключенным в скобки, обозначающие абсолютную  величину вектора -

 



 

Рис.1.2. Изображение вектора силы

 

Модуль силы в общепринятой в  настоящее время системе единиц СИ измеряется в ньютонах (Н), применяются и более крупные  единицы - килоньютон( 1кН = 10³ Н), меганьютон (1мН=10⁶Н).

 Прямая, совпадающая с вектором силы, называется линией действия силы.

Система сил - это любая их совокупность. Как  правило, система сил характеризуется каким-либо признаком. Различают сходящуюся систему сил (линии действия которых пересекаются в одной точке), плоскую (лежат в одной плоскости), пространственную, систему параллельных сил и т.д.

Основными задачами статики являются:

1. Приведение данной системы сил к простейшему виду (упрощение).

2. Исследование условий равновесия данной системы сил.

Равновесие (покой) является частным случаем движения, то есть изменения положения одних тел по отношению к другим телам.

Эквивалентными системами сил называются такие системы, которые оказывают на тело одно и то же действие.

Уравновешенной называется  система  сил, действие которой эквивалентно нулю.

Равнодействующая - это сила, действие которой эквивалентно действию данной системы сил.

В статике  рассматриваются, как  правило, абсолютно твердые тела, расстояние между двумя любыми точками которых  остается постоянным. На  самом  деле это является абстракцией, так как любое твердое тело  под  действием  нагрузки  деформируется, однако во многих случаях  величиной  деформаций можно пренебречь.

 

1.2.Аксиомы статики

 

Все уравнения  статики  выводятся  из нескольких исходных положений - аксиом, то есть математически недоказуемых положений. Они представляют собой результаты обобщений практической деятельности.

1. Если на свободное  твердое  тело действуют две силы, то тело может находиться в равновесии, если эти силы равны по  величине и направлены по одной прямой в разные стороны (рис.1.3).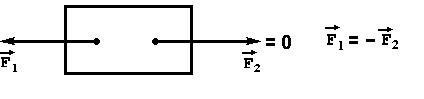

 





Рис.1.3. Первая аксиома статики

 

2. Действие данной системы сил не изменится, если  к  ней добавить или от нее отнять уравновешенную систему сил.

Следствие: не изменяя действие силы,  ее  можно  переносить вдоль линии действия. Доказательство приведено на рис.1.4.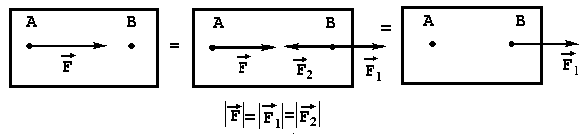

 





Рис.1.4. Следствие второй аксиомы статики

 

Итак, имеем силу  , приложенную в точке А. Приложим в произвольной точке В, лежащей на линии действия силы  , уравновешенную систему сил   и  , модули которых равны модулю силы  . Затем уберем уравновешенную систему сил   и  . Таким образом, на тело останется действовать одна сила  , равная по модулю силе  , но приложенная в точке В, то есть, не изменяя действия силы  , ее перенесли из точки А в точку В.

3. Аксиома параллелограмма. Две  силы, приложенные  в  одной точке, имеют  равнодействующую, приложенную в той же точке,  по величине и направлению равную диагонали  параллелограмма, построенного на этих силах, как на сторонах (рис.1.5).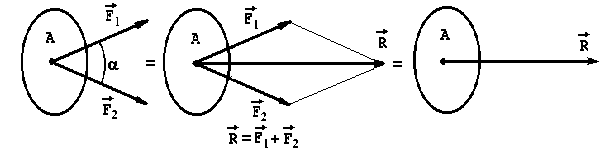

 





Рис.1.5. Аксиома параллелограмма

 

Вектор   называется геометрической суммой этих сил.

Модуль его можно найти, применяя теорему косинусов

 





 

На основании данной аксиомы одну силу можно заменить двумя силами, что часто применяют в статике.

4. Два тела взаимодействуют с силами, равными по величине и противоположными по направлению (рис.1.6.). Это не зависит  от того, касаются ли тела  друг друга непосредственно или взаимодействуют на расстоянии.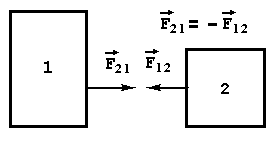





Рис.1.6. Аксиома равенства действия и противодействия

 

 

 

1.3.Связи и их реакции

 

Рассматриваемые в механике тела могут быть  свободными  и несвободными. Свободным называется тело, которое не  связано  с другими телами  и  может  совершить из данного положения любое перемещение в пространстве. Тело, перемещение которого хотя бы в одном направлении ограничивается в пространстве другими телами, называется несвободным.

Тела, которые препятствуют перемещению данного тела , называются связями, а силы, с которыми связи действуют на это тело, - реакциями связей. Реакция связи всегда направлена противоположно тому направлению, по которому связь препятствует перемещению тела. Рассмотрим простейшие виды связей.

1. Гибкая связь (нить, трос, цепь и т.д.). Поскольку нить ограничивает перемещение подвешенного к ней тела только в  одном направлении (вдоль нити от точки подвеса), то реакция нити также направлена вдоль нити, но к точке подвеса (рис.1.7). Нить может только растягиваться.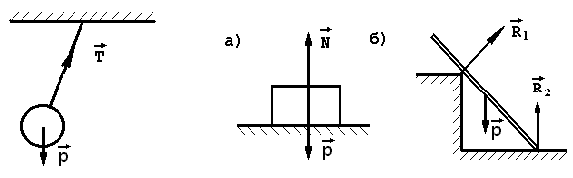





 

Рис.1.7.Гибкая связь                           Рис.1.8. Гладкая поверхность

 2. Гладкая (без  трения) поверхность  (опора). В этом случае реакция направлена по нормали к поверхности  (рис.1.8,а). Если одно  из тел касается другого в точке, то реакция направлена по нормали к другому телу (рис.1.8,б).

3. Тонкий невесомый стержень с шарнирным закреплением концов. Поскольку стержень находится в  равновесии  под  действием двух сил, приложенных  к  его концам, то согласно первой аксиоме статики эти силы должны быть направлены по одной прямой, следовательно, реакция стержня на тело будет направлена вдоль стержня  (рис.1.9). В отличие от нити стержень может быть как сжат, так и растянут.

Одной из важных задач статики является определение  реакций связей. Для этого используется принцип (аксиома) отбрасывания связей: каждое несвободное тело можно считать свободным, если отбросить  связи  и  заменить  их действие реакциями связей (рис.1.10). При решении задач  новый  рисунок, как правило, не делается, а реакции показываются прямо на связях.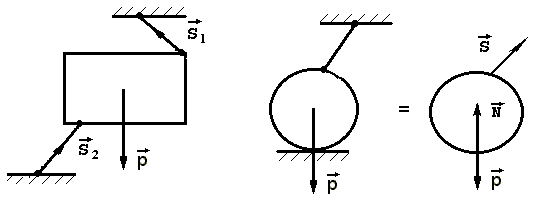

 





 Рис.1.9. Тонкий невесомый           Рис.1.10. Аксиома отбрасывания связей

                  стержень

 

1.4. Действия с силами

 

С силами, как  и с любыми векторами, можно проводить операции геометрического сложения  и  разложения. Сложить  две  силы можно, используя  аксиому  параллелограмма  сил, строя диагональ параллелограмма на этих силах, как на сторонах. Если нужно  сложить несколько  сил, то  следует  построить силовой многоугольник, прикладывая каждую последующую силу к концу предыдущей. Замыкающая сторона силового многоугольника и будет равна геометрической сумме этих сил. Заметим, что этот вектор всегда направлен из  начала  первой  силы  к  концу последней, а не наоборот (рис.1.11).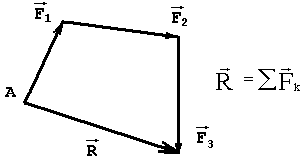

 





Рис.1.11. Сложение сил

 

Величина, равная  геометрической  сумме всех сил данной системы, называется главным вектором этой системы.

Решение задач  статики геометрическими методами сопряжено с громоздкими построениями. Более простыми являются так называемые аналитические методы, в которых все операции проводятся не с векторами, а с числами. Для этого  вводится  понятие  проекции вектора силы на ось.

Проекцией силы на ось называется скалярная  величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца вектора силы. Проекция считается положительной, если  направление  от начала к концу проекции совпадает с положительным направлением оси (рис.1.12).

Из рисунка  видно, что проекция силы на ось равна произведению модуля силы на косинус угла между силой и  положительным направлением оси.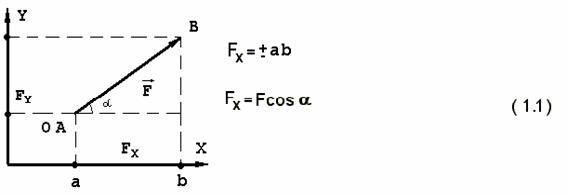

 





Рис.1.12. Проекция силы на ось

 

Частные случаи проектирования.

1. Сила образует  острый угол с положительным направлением оси (рис.1.12). В этом случае проекция положительна (F_x>0, F_y>0).

2. Сила перпендикулярна оси (рис.1.13,а). Поскольку в этом случае cos()=0, то и проекция силы на эту ось равна нулю: F_x=0.

 





Рис.1.13. Частные случаи нахождения проекций сил

 

3. Сила параллельна  оси. Поскольку угол между силой и осью равен нулю, а косинус нуля равен единице, то проекция будет равна  модулю силы: F_у = F (рис.1.13,а).

4. Сила образует тупой угол с  положительным  направлением оси (рис.1.13,б). В  этом  случае

 

F_x = Fcos() = Fcos(180-)= -Fcos(),

 

то есть проекция отрицательна.

         Зная величины  проекций  силы на взаимно перпендикулярные оси Х,  У и Z, модуль силы можно вычислить с помощью теоремы  Пифагора (рис.1.14).





Так как    , а    , то

 

 .                                          (1.2)





Рис.1.14. Разложение силы по осям координат

 

С помощью  проекций  можно  находить  не только силы, но и сумму сил. Рассмотрим силы  ,   и  . Строя векторный  многоугольник, найдем векторную сумму этих сил (рис.1.15).

 





Рис.1.15. Сложение сил

 

Из рисунка видно, что проекция  вектора  суммы  сил  равна сумме проекций сил на эту же ось

 

R_x= F_1x+F_2x+F_3x,

 

 или                                        R_х =F_кх.

 

Аналогично,

R_y =F_кy., R_z =F_кz

 

Тогда, учитывая формулу (1.2), модуль  суммы сил равен

 

.                                (1.3)

  

1.5. Сходящаяся система сил

 

Рассмотрим систему сил, линии действия которых пересекаются в точке А (рис.1.16). После переноса точек приложения сил в точку А можно последовательно сложить все  силы, строя силовой многоугольник, таким образом заменяя все силы одной равнодействующей.

Следовательно, система сходящихся сил имеет равнодействующую, приложенную в точке пересечения сил и равную геометрической сумме всех сил  данной системы.





Рис.1.16. Приведение сходящейся системы сил к простейшему виду

 

Вторая задача статики - разработка условий равновесия. Они могут быть получены в двух видах:

1. Геометрическое условие. Очевидно, что система  сходящихся сил будет эквивалентна нулю, если силовой многоугольник, построенный из сил системы, будет замкнут. В этом случае 

2. Аналитическое условие. Из формулы (1.3) следует, что величина равнодействующей   будет равна нулю, если выполняются  условия

 

F_кx=0; F_кy=0; F_кz=0.                        (1.4,а)

 

Выражения (1.4,а) являются уравнениями  равновесия сходящейся системы сил: система сил находится в равновесии, когда алгебраическая сумма  проекций  всех  сил системы на оси  Х , У и Z равна нулю.

Если все силы лежат в одной плоскости ( плоская сходящаяся система сил), то последнее из равенств (14,а) превращается в тождество и остаются два значащих уравнения

 

F_кx=0; F_кy=0.                               (1.4,б)

 

1.6.Решение задач

 

Для решения задач статики можно воспользоваться следующим планом.

1. Выбрать объект, равновесие  которого  следует   рассмотреть. Таким объектом может быть точка, тело либо система тел.

2. Приложить действующие на этот объект силы.

3. Отбросить связи, заменив их действие реакциями .

4. Определить тип  полученной  системы   сил. Убедиться, что число неизвестных в задаче равно числу уравнений равновесия, то есть выяснить статическую определимость задачи.

5. Выбрать оси  координат. При  выборе  осей  следует  помнить, что уравнение будет проще, если в него входит меньшее  количество неизвестных, то  есть  необходимо по возможности оси координат брать перпендикулярно одной из неизвестных реакций.

6. Составить уравнения равновесия, соответствующие данному виду системы сил, и решить их относительно неизвестных.

Пример (рис.1.17). Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити  подвешен груз весом 100 Н. Определить усилия в стержнях.

Решение. Поскольку стержни соединены  в точке В, она  будет служить объектом  равновесия. Hа нее будет действовать  сила натяжения нити, равная весу груза.

Связями  для  точки В служат стержни АВ и ВС. Отбрасывая связи, заменим их  реакциями - и  , которые направлены вдоль стержня. Направляя усилия  от точки В, предполагаем, что оба стержня растянуты. На точку В действуют три  силы, лежащие в одной плоскости и пересекающиеся в одной точке, то есть плоская сходящаяся система сил, для которой  можно  составить два  уравненияравновесия

 

                            F_кx=0    , F_кy=0.

 

. 

Рис.1.17. Аналитический способ решения

 

         В этих  уравнениях  находится два неизвестных - усилия S₁ и S₂. Оси координат направим вдоль стержней. Составляем  уравнения равновесия:

 

F_kx=S₁-Pcos(60)=0;

 

F_ky=S₂+Pcos(30)=0.

 

Из первого уравнения находим

 

                   S₁=P cos(60)=1000,5=50 H,

 

 из второго:         S₂= - Pcos(30)= - 1000,866= - 86,6 H.

 

Усилие S₂ получилось отрицательным, то есть стержень ВС будет не  растягиваться, а сжиматься.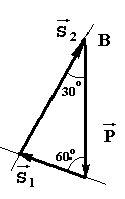



Рис.1.18. Геометрический способ решения

 

В данном  решении  использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В, векторный треугольник. Вначале в масштабе построим  силу  Р  (рис.1.18).   Из  начала и конца этой силы проводим прямые, параллельные усилиям   и  , получая таким образом замкнутый силовой треугольник. При этом для замыкания треугольника  мы были вынуждены сменить направление  усилия  . Из  треугольника, в  котором усилие Р  является  гипотенузой, а S₁ и  S₂  - катетами, находим

 

S₁=Pcos(60)=50 H,      S₂=Pcos(30)=86,6 H.

 

1.7. Моменты силы относительно точки и оси

 

Сила может не только перемещать тело  поступательно, но  и оказывать на  него  вращательное  действие, которое  зависит не только от величины силы, но и от расстояния до  центра  поворота.   Например, для того, чтобы повернуть тело  с помощью рычага (рис.1.19), наименьшую по модулю силу нужно приложить к концу рычага. Чем ближе к центру, тем величина силы  должна быть больше, если  же сила будет проходить через точку  О, то повернуть тело будет невозможно, какой большой бы  она ни была.

 





Рис.1.19. Вращательное действие силы

 

Для характеристики вращательного действия силы вводится понятие момента силы относительно точки.

Моментом силы относительно точки называется  алгебраическая величина, равная  произведению  модуля  силы  на кратчайшее расстояние между точкой и линией действия силы (плечо)

 



                                                  .                                     (1.5)

 

Знак момента определяется следующим образом: если  сила стремится повернуть тело вокруг данной точки против часовой стрелки, то он считается положительным (рис.1.20), в противном случае - отрицательным.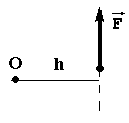



Рис.1.20. Момент силы относительно точки

 

Момент силы относительно точки равен нулю только в том случае, если линия действия силы проходит через данную точку. Единицы измерения момента [HM] и в соответствующих кратных единицах.



         Момент силы относительно оси характеризует вращательное действие силы относительно оси. Если силу F разложить  на  составляющие   и  , одна из которых параллельна, а другая  перпендикулярна оси Z (рис.1.21), то увидим, что сила   не способна повернуть тело вокруг оси, а вращательное действие силы   определится ее моментом относительно  точки  О.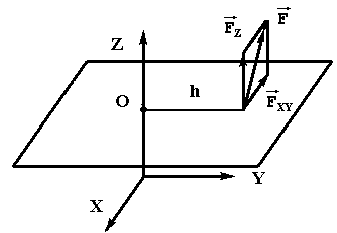





Рис.1.21. Момент силы относительно оси

 

 Следовательно, для  определения момента  силы  относительно оси  нужно силу спроектировать на плоскость, перпендикулярную оси, и найти  момент проекции относительно точки пересечения оси с этой плоскостью

 

                                                (1.6)

 

Знак момента определяется следующим образом: момент  считается положительным, если, глядя с положительного конца оси, можно увидеть поворот тела будет виден против часовой стрелки. Момент силы  относительно оси  равен нулю, если сила параллельна оси или пересекает ее.

При определении момента силы относительно точки часто бывает затруднительно определить плечо силы. В этом случае можно воспользоваться теоремой Вариньона: момент равнодействующей плоской системы сил относительно  точки  равен алгебраической сумме моментов составляющих сил относительно той же точки

 



                                                .                              (1.7)

 

Аналогичная теорема  применима  и для определения момента силы относительно оси.

Пример: найти момент силы F = 10 H  относительно точки А, если АВ=0,2 м, ВС=0,5 м (рис.1.22). Разложим силу F на две  составляющих F_x=Fcos(30), F_y=Fsin(30).

 

Тогда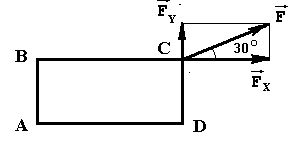                      

 





Рис.1.22. Пример применения теоремы Вариньона

 

Или



 

1.8. Пара сил и ее свойства

 

Парой сил называется система, состоящая из двух сил, равных по модулю, противоположных по направлению и не лежащих на одной прямой (рис.1.23).

Плоскость, в которой лежат силы пары, называется плоскостью действия пары, а кратчайшее расстояние между силами пары называется плечом пары.         Сумма сил пары равна нулю, поэтому пара сил не имеет равнодействующей, однако она  оказывает  на тело вращательное действие, характеризуемое ее моментом.

                  





Рис.1.23. Пара сил

 

Моментом  пары называется алгебраическая величина, модуль  которой равен произведению одной  из сил на плечо пары

 

                                      m =F₁d =F₂d.                                      (1.8)

 

Момент пары считается положительным, если  пара  стремится повернуть тело против часовой стрелки, и отрицательным, если пара стремится повернуть тело по часовой стрелке.

         Эффект действия пары на твердое тело не зависит от ее положения в плоскости, поэтому ее можно  переносить  в  плоскости действия в любое положение. Кроме того, не изменяя действия пары на тело, ее можно заменить другой парой с равным  моментом. Поэтому часто пары изображают в виде круговой стрелки и называют пару сосредоточенным моментом (рис.1.24).





 

Рис.1.23. Эквивалентность пар

 

Поскольку действие  пары определяется ее моментом, то если на тело действует несколько пар, лежащих в  одной  плоскости, то их можно заменить одной парой с моментом, равным сумме моментов слагаемых пар: М=M_k. Отсюда следует условие равновесия системы пар, лежащих  в одной плоскости: для равновесия системы пар необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю

 

M_k=0.                                           (1.9)

 

Отметим еще одно важное свойство пары  сил: сумма  моментов сил пары относительно любой точки равна моменту  пары. Возьмем пару сил F₁ и F₂ и  произвольную точку А (рис.1.25).





Рис.1.25. Свойство моментов сил пары

Тогда

 




1.9.Теорема о параллельном переносе силы

 

Данная теорема  позволяет  упростить  действующую на тело систему сил. Рассмотрим силу F, приложенную в точке А (рис.1.26).

 



Рис.1.26. Теорема о параллельном переносе силы

 

Приложим в произвольной точке  В  уравновешенную  систему сил   и  , по модулю равных F и параллельных к ней. Тогда силы 

и   образуют пару сил, которую отобразим в виде момента М.

В результате   имеем систему, состоящую из силы  , приложенной в точке В, и равную по модулю  , и пару  сил  с  моментом М, равным моменту  силы F относительно точки В. Таким образом, мы доказали теорему: не изменяя действия силы на тело ее  можно перенести параллельно самой себе в любую точку, добавляя  при этом пару сил с моментом, равным моменту этой силы относительно точки, в которую  она переносится.

 

1.10. Плоская произвольная система сил

 

Полученная теорема  позволяет  решить  задачу  упрощения плоской системы сил. Допустим, на тело действует система сил  ,  , ... ,   (рис.1.27).





Рис.1.27. Приведение плоской системы сил к простейшему виду

 

         Выберем произвольную  точку  О, которая называется центром приведения, и, используя теорему о параллельном переносе силы, перенесем все  силы в точку О, добавляя при этом пары сил с моментами, равными моментам  сил  относительно этой точки. Тогда получим в точке О сходящуюся систему сил и систему пар. Эти силы заменим одной силой, равной геометрической сумме всех  сил, а пары - одной  парой, с моментом, равным сумме моментов всех сил системы относительно центра приведения (главному моменту системы относительно точки О).

Таким образом, приводя плоскую систему сил к центру, ее можно заменить системой, состоящей из одной силы и одной пары.

         Отсюда следует, что данная система будет находиться в равновесии, если результирующая сила и момент результирующей пары будут равны нулю. Аналитически сила будет равна нулю, если равны нулю ее проекции на оси Х и У, то есть для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси Х и У и сумма моментов всех сил относительно произвольной точки были равны нулю

                                    F_kx=0;       F_ky=0;    m₀ =0.      (1.10)

                                        

 

Формулы (1.10) называются уравнениями  равновесия плоской системы сил.

 

1.11. Опорные устройства балок

 

Балкой называется  тело, размерами сечения которого по сравнению с длиной можно пренебречь и которое предназначено, главным образом, для восприятия поперечных нагрузок. Связями для балок могут служить рассмотренные ранее гибкие связи, стержни и гладкие поверхности, но, как правило, применяются и специальные опорные устройства. Рассмотрим три вида опорных устройств.

1. Шарнирно подвижная опора (рис.1.28,а). Такая опора допускает поворот  вокруг оси шарнира и линейное перемещение, параллельное опорной поверхности. Следовательно, реакция направлена перпендикулярно опорной поверхности.

2. Шарнирно неподвижная опора (рис.1.28,б). Эта опора допускает только поворот вокруг оси шарнира и препятствует перемещению закрепленного в ней тела в любом направлении, поэтому и направление реакции неизвестно. Обычно вместо определения полной реакции ее разлагают на две составляющих.

 



Рис.1.28. Опорные устройства балок

 

3. Жесткая заделка (рис.1.28,в). Заделка препятствует повороту и любому перемещению балки, поэтому неизвестна не только величина и направление реакции, но и ее точка приложения. Приводя все реактивные силы к точке А, заменяем их реакцией  , которую разлагаем на составляющие  и  , и парой сил с моментом m_a, который называется реактивным моментом.

 

1.12.Распределенная нагрузка

 

При решении практических задач далеко не всегда можно считать, что действующая на тело сила приложена в одной точке. Часто силы бывают приложены на целом участке  тела (например, снеговая нагрузка, ветровая и т.д.). Такая нагрузка называется распределенной. Равномерно распределенная нагрузка характеризуется интенсивностью q (рис.1.29).              Интенсивность - это суммарная нагрузка, приходящаяся на единицу длины конструкции.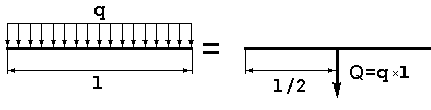





Рис.1.29. Распределенная нагрузка

 

Единица измерения интенсивности - [H/м], [кН/м]. При решении задач статики распределенную нагрузку можно заменить ее равнодействующей, которая равна произведению интенсивности на длину участка, на который действует распределенная нагрузка, и которая приложена в середине этого участка.

 

1.13. Решение задач на плоскую систему сил

 

Пример (рис.1.30). Определить реакции шарнирно опертой балки, нагруженной силой   и парой сил с моментом М.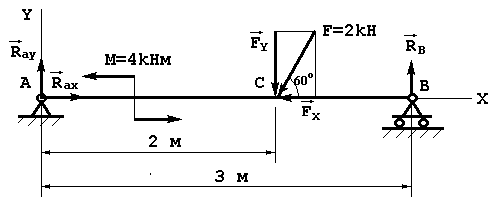





Рис.1.30. Рисунок к примеру

 



Решение. Воспользуемся тем  же  планом, который применялся для решения задач на сходящуюся систему сил. Объектом равновесия является вся балка, нагрузка на которую показана на чертеже. Отбросим связи - шарниры А и В. Реакцию неподвижного шарнира А разложим на две составляющих -  и  , а реакция подвижного шарнира В будет направлена перпендикулярно опорной плоскости. Таким образом, на балку действует плоская произвольная система сил, для которой можно составить три уравнения равновесия. Выберем оси координат и составим эти уравнения.

Уравнения проекций

 

1. F_kx = 0;            R_ax  -Fcos(60) = 0;

 

2. F_ky = 0;            R_ay + R_B - Fcos(30) = 0

 

(пара в уравнение проекций не входит, так как сумма проекций сил пары на любую ось равна нулю).

Уравнение моментов составляем относительно точки А, поскольку в ней пересекаются две неизвестные силы. При нахождении момента пары относительно точки А помним, что сумма моментов сил пары относительно любой точки равна моменту пары, а знак момента будет положительным, поскольку пара стремится повернуть тело против часовой  стрелки. Для нахождения момента силы   удобно разложить ее на вертикальную и горизонтальную составляющие

 

F_x=Fcos(60), F_y=Fcos(30)

 

и воспользоваться теоремой Вариньона, причем следует  учесть, что момент от силы  относительно точки А равен нулю, поскольку ее линия действия проходит через эту точку. Тогда уравнение моментов примет вид:

 

3.  ;       R_в^.3-F_Bcos(30)2 + M = 0.

 

Решая это уравнение, получим

 





 

Из уравнения (2) находим

 

R_ay = Fcos(30) - R_B = 20,866 - 4=-2,67 кН,

 

а из уравнения (1)         R_ax = Fcos(60) = 20,5 = 1 кН.

 

Пример. Определить реакции жестко защемленной балки длиной 3 м,  нагруженной равномерно распределенной нагрузкой интенсивностью q=10кН/м (рис.1.31).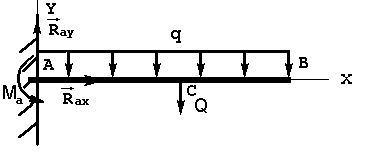

 

 





Рис.1.31. Рисунок к примеру

 

         Решение. Заменим равномерно распределенную  нагрузку ее равнодействующей Q  = 3q = 310 = 30 кН. Она будет приложена в середине пролета, то есть на расстоянии АС = 1,5 м. Рассматриваем равновесие балки АВ. Отбрасываем связь - жесткую заделку, а вместо нее прикладываем две составляющие реакции R_ах  и  R_ау и реактивный момент M_а. На балку будет действовать плоская произвольная система сил, для которой можно составить три  уравнения равновесия и из них можно найти искомые неизвестные:

 

F_кх = 0;                R_ах  = 0;

 

F_ку = 0;         R_ау  - Q = 0;            R_ау = Q = 30 кН;

 

M_а(F_к) = 0;  M_а - 1,5Q = 0; M_а =1,5Q =1,530 = 45 кHм.