обработка_ЭД_лекция_5. 2 Вероятность случайных событий, их характеристики
 Скачать 78.28 Kb. Скачать 78.28 Kb.
|
|
2.1. Вероятность случайных событий, их характеристики При анализе погрешностей эксперимента и обработке результатов широко используется аппарат математической статистики и теории вероятностей, поэто-му напомним некоторые основные понятия и определения теории вероятностей и математической статистики. Случайной называется величина, принимающая в результате эксперимента некоторое значение, заранее неизвестное. Пусть проведено n измерений признака Х, в результате получим ряд изме-рений (например, температура сваривания кожи), отличающихся друг от друга
где xi – "i"-е измерение величины Х; х1, х2,..., хn – реализация случайной ве-личины Х. Случайная величина может быть непрерывной и дискретной. Случайная ве-личина Х называется непрерывной, если она может принимать любые значения в некотором интервале числовой оси (например, продолжительности процессов отмоки, сушки и т.п.). Дискретная случайная величина Х принимает конечное или счетное, строго определенное число значений с определенной вероятностью (число шкур в партии, количество штук рулонов ткани за единицу времени, например, за месяц или смену). Полностью свойства случайной величины описываются законом распреде-ления. Под законом распределения понимают связь между возможными значениями случайной величины и соответствующими им вероятностями. Мерой вероятности дискретной случайной величины может служить частота наступления событий:
(2.2) где Рi – вероятность "i"-го события; mi – число наступлений "i"-го события в испытаниях; n – общее число испытаний. При возрастании nN (где N – большое число) отношение mi/n принимает все более устойчивое значение, т.е. становится статистически устойчивым. Предел, к которому стремится отношение mi/n при неограниченном возрастании числа экспериментов (испытаний) n, называют вероятностью случайного события 1
Говорят, что действует закон больших чисел. Таким образом, частота слу-чайного события – это отношение числа появления этого события к общему числу произведенных испытаний. Нетрудно заметить, что 0 i<1. Если Рi=0, то событие невозможно, Рi=1 – достоверно. Пример 2.1. Требуется определить вероятность числа передубливаний (нарушений технологического процесса), исходные данные представлены в табл. 2.1, а результаты расчета – на рис.2.1. Таблица 2.1 Число (количество раз) передубливаний по месяцам (общее число испытаний n=18 - полгода)
По графику, представленному на рис.2.1, можно сделать некоторые выводы. Так, наиболее вероятное число передубливания равно 5, а вероятность наступления этого события в диапазоне от 2 до 5 включительно составляет 0,67. Заметим, что эти выводы сделаны на основании весьма ограниченного числа наблюдений, равного 18. Как же оценить достоверность и надежность полученных результатов? Как изменится их достоверность при увеличении числа измерений? Сколько же измерений (наблюдений) при этом следует провести? Теория инженерного эксперимента, как мы увидим в дальнейшем, позволяет дать ответ на эти вопро-сы. 2 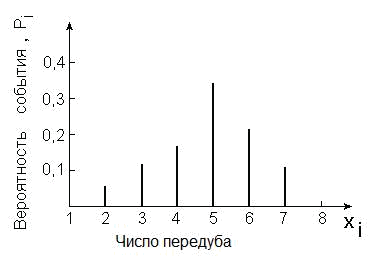 Рис.2.1. Вероятность передубливания материала в процессе дубления Различают два вида описания законов распределения: интегральный и диф-ференциальный. Для характеристики непрерывной случайной величины используется инте-гральная функция распределения F(x) – это вероятность того, что случайная величина Хх, т.е. X x
Интегральная функция распределения имеет следующие свойства (рис.2.2):
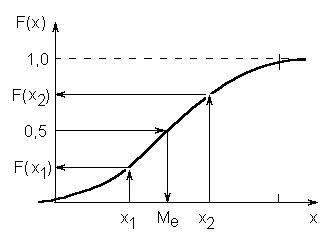 Рис.2.2. Интегральная функция распределения: F(x2)-F(x1)=P(x1xx2) 3 Она представляет собой монотонно возрастающую кривую. Если х2>х1, то F(x2)>F(x1). Ордината этой кривой, соответствующая точке х1, представ-ляет собой вероятность того, что случайная величина х будет меньше х1. F(x1)=P(x Ее приращение в промежутке (х1;х2) равно вероятности для величи-ны X попасть в этот промежуток:
Дифференциальный закон распределения (плотность распределения) выра-жается соотношением (рис.2.3)
то есть она характеризует приращение вероятности (ее скорость) при изме-нении значений случайной величины Х на единицу.  Рис.2.3. Дифференциальный закон распределения(плотность распределе-
Площадь, заключенная под кривой плотности распределения, со-гласно правилу нормировки, равна единице, т.е. отражает вероятность всех возможных событий. f Z dZ 1 .
4
Часто для характеристики случайной величины используют не сами функ-ции распределения, а некоторые числовые параметры – параметры распределения (рис.2.4). Важнейшими параметрами распределения, характеризующими случай-ную величину х, являются ее математическое ожидание Mx (центр рассеивания) и дисперсия x2 (степень рассеивания). Рассмотрим характеристики положения центра распределения изучаемой случайной величины. Для непрерывной случайной величины математическое ожидание опреде-ляется выражением
где х – значение непрерывной случайной величины; f(x) – плотность веро-ятности. Важно знать геометрическую интерпретацию математического ожида-ния – это абсцисса центра тяжести кривой распределения плотности вероятности f(x), т.е. дифференциального закона распределения.  Рис.2.4. К характеристикам рассеивания случайной величиныДля дискретной случайной величины
где N – достаточно большое число; xi– значение "i"-й дискретной случайной величины; Pi – вероятность ее реализации. 5 Сказанное проиллюстрируем на рис. 2.3, где видно, что произведение f(x)dx есть площадь элементарного участка под кривой f(x), а x – абсцисса этого участ-ка, т.е. расстояние от начала координат. Следовательно, интеграл (2.8) даст абсциссу центра тяжести всей площади под кривой f(x). Для рассмотренного ранее примера 2.1 величина Mx=4,88 и не равна ни од-ному из значений дискретной случайной величины (следовательно, оно может быть дробным). Модой Мo непрерывного распределения называют значение аргумента, при котором плотность распределения f(x) достигает максимума или это значение случайной величины, имеющей максимальную вероятность в том случае, когда случайная величина дискретная (для рассмотренного примера Mo=5). Медиана Ме – это значение аргумента, при котором число элементов совокупности со значением данного признака больше этой величины равно числу элементов со значением признака меньше ее. Для непрерывной случайной величины медиана определяется из решения уравнения: e F ( M e ) f ( x ) dx 0 ,5. или для дискретной случайной величины e P ( x i ) 0 ,5; x i M e . 1 (2.10) (2.11) Таким образом, для дифференциального закона распределения медиана есть такое значение непрерывной случайной переменной x, которая делит пополам площадь под кривой распределения f(x). Кроме характеристик положения центра, используются другие характери-стики, описывающие рассеивание случайных величин. Важнейшей из них являет-ся дисперсия (см. рис. 2.4). Дисперсия для непрерывной случайной величины определяется соот- ношением
где х – непрерывная случайная величина; f(х) – плотность вероятности. Для дискретной случайной величины
где хi– реализация "i"-й случайной величины; N – достаточно большое чис- ло. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно среднего значения (математического ожидания). Положительное значение квадратного корня из дисперсии называется среднеквадратичным отклонением
2.2. Нормальный закон распределения Функции распределения F(x) и f(x) представляют собой математическую модель, которая описывает экспериментально наблюдаемые величины. Одной из задач статистической обработки данных является нахождение таких функций распределения, которые, с одной стороны, достаточно хорошо описывали бы наблюдаемые значения случайной величины, а с другой – были бы удобны для дальнейшего статистического анализа. Вид функции распределения предпочти-тельно выбирать на основе представлений о физической природе рассматривае-мого явления, т.к. в этом случае исключаются возможные погрешности при распространении найденных закономерностей за пределы изучаемого интервала варьирования случайных величин. Среди всех изученных до настоящего времени случайных величин наиболее важное место занимают случайные величины, имеющие так называемое нормаль-ное (Гауссово) распределение (рис.2.5). Нормальному закону подчиняются, как правило, результаты испытаний материала на прочность, производительность многих агрегатов в легкой промышленности, составы сырья, реагентов, площади материала, вырезанные по одинаковым лекалам, случайные ошибки измерений и т.п., поэтому исследователи чаще всего используют это распределение при математической обработке результатов наблюдений. Другие распределения, которые мы будем использовать в дальнейшем (Стьюдента, Фишера, Пирсона) составлены на основе именно нормального распределения. Заметим, что в математической статистике сделана оценка для двух противоположных распределений: нормального и равномерного и показано, что оценки результатов исследований в технических задачах отличаются не более, чем на 20% . 7 ряде случаев важно знать вероятность того, что случайная величина Х не будет отличаться от своего среднего значения Мx больше, чем на величину . Эта вероятность называется доверительной вероятностью (P) и она показывает вероятность того, что результат измерений отличается от истинного значе-ния на величину, не большую :
Интервал от (Mx-) до (Mx+) называется доверительным интерва-лом. В дальнейшем уточним эти понятия. Заметим, что доверительная вероятность равна площади, заштрихованной на рис.2.6. Действительно, площадь, ограниченная интервалом , равна вероят-ности того, что случайная величина находится в этих пределах. Обозначим значение доверительного интервала, выраженного в долях среднеквадратичного отклонения, как
Тогда, в случае использования нормированного значения случайной величины, выражение (2.21) примет вид
 Рис.2.6. К понятию доверительного интервала Эта функция называется нормированной функцией Лапласа и для об- легчения расчетов эта функция представлена таблицами и приведена в справоч-ной литературе. Так, доверительному интервалу, равному значению среднеквад-ратичного отклонения (=x=1x), соответствует доверительная вероятность 8 0,68. Иными словами, при нормальном законе распределения примерно 2/3 всех значений случайной величины (наблюдений) лежит в площади, отсекаемой перпендикуляром к оси ОХ (Mx=x). Доверительному интервалу равному =1,96x2x, соответствует доверительная вероятность 0,95. Доверительному интервалу 3x соответствует доверительная вероятность 0,997. Следовательно, отклонение истинного значения случайной величины от ма-тематического ожидания не превосходит утроенного среднего квадратичного отклонения с вероятностью 0,997. Это свойство в математической статистике носит названия правила трех сигм. Отметим дополнительно, что 90% значений случайной величины лежат в диапазоне между -1,64x и +1,64x. Таким образом, чем больше величина довери-тельного интервала , тем с большей вероятностью величина x попадает в этот интервал. 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
