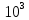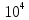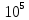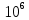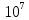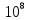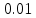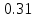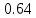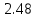апюьсВсkhj. Вычисление интегралов методом статистических испытаний (с поясне. Целью данной работы
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
ВВЕДЕНИЕМетодом Монте – Карло называют численный метод, основанный на моделировании случайных величин для решения математических задач. Методы Монте – Карло применяются для решения прикладных задач в различных предметных областях: квантовая физика, экономика, инвестиционных прогнозах и финансовое планирование, теория игр, математика и др. Метод статистических испытаний занимает особое положение среди методов вычисления определенных интегралов, особенно, сложных интегралов, которые еще называют «неберущимися». Целью данной работы является применение метода статистических испытаний для решения задач прикладного характера, сводящихся к нахождению значения определенного интеграла. В связи с поставленной целью были сформулированы следующие задачи: Изучить теоретических основ метода (основные понятие теории вероятности и математической статистики) Рассмотреть некоторых способов вычисления площади методом Монте – Карло (метода усреднения подынтегральной функции и способ, основанный на истолковании интеграла как площади) Написать программу на языке программирования Python для каждого из рассмотренных способов. Произвести расчеты и занести данные в таблицы. Проанализировать полученные результаты и сравнить способы реализации метода Монте – Карло. Сделать выводы Объект исследования: значения определенных интегралов, возникающих при решении прикладных задач, а также значения «неберущихся» интегралов (интеграл Лапласа). Предметом исследования является метод Монте – Карло или метод статистических испытаний. Вычисление значений определенных интегралов методом Монте – Карло освещается в [1-5]. Понимание вычисления значения довольно простого определенного интеграла, используется для более сложной задачи – нахождения значений интеграла Лапласа, относящегося к «неберущимся» интеграла, таблицы значений которого приводятся в книгах [1, 2]. ГЛАВА 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ1.1. Некоторые сведения из теории вероятностей и математической статистикиИспытанием называют осуществление некоторых действий. Факт, который может произойти при проведении испытаний называют событием. Исходом называют любой результат испытания. Благоприятным называется исход, способствующий наступлению рассматриваемого события. Множество всех различных исходов произвольного испытания называют множеством элементарных событий. Вероятностью случайного события A называется отношение числа элементарных событий m, которые благоприятствуют этому событию к общему числу всех элементарных событий n. 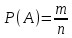 Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной называют случайную величину, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Математическим ожиданием дискретной случайной величины называют: 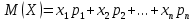 , ,где 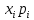 – произведение ее возможных величин на их вероятности. – произведение ее возможных величин на их вероятности.Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. (При вычислении значений интегралов методом Монте – Карло важную роль играют именно непрерывные случайные величины, ведь мы рассматриваем функцию на отрезке, а не в отдельных точках) Число возможных значений непрерывной случайной величины бесконечно. 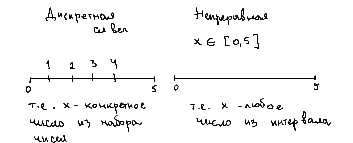 Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат интервалу 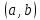 , определяется равенством , определяется равенством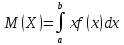 , , где 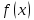 – плотность распределения случайной величины X. – плотность распределения случайной величины X.Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: (разброс от математического ожидания, т.е. находится среднее арифметическое всех точек до математического ожидания, например см.рис): 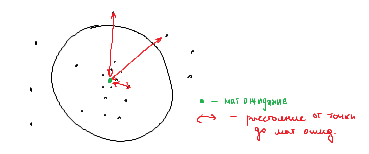 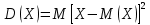 Средним арифметическим чисел называется частное от деления суммы этих чисел на число слагаемых 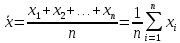 Статистическая погрешность — это неопределенность в оценке истинного значения измеряемой величины, возникающая при нескольких повторных измерениях одним и тем же инструментом. При этом результаты измерений различаются, так как имеют вероятностный характер. Находится она по формуле: 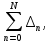 где 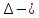 абсолютная погрешность, которая является модулем разности между измеренной величиной и ее действительным значением абсолютная погрешность, которая является модулем разности между измеренной величиной и ее действительным значением 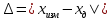 1.2. Сущность метода Монте – КарлоСущность метода Монте – Карло заключается в следующем. В методе строится последовательность случайных чисел или их наборов. Каждый новый элемент последовательности проверяется на выполнение ряда условий, которые позволяют или не позволяют соотнести это число (или набор чисел) последовательности с некоторым событием, называемым в теории вероятности благоприятным исходом. Именно поэтому метод Монте – Карло называют еще и методом статистических испытаний, так как применение метода позволяет установить на основе многократного повторения случайных событий в рассматриваемой модели математические связи. Пусть требуется найти значение aнекоторой рассматриваемой величины. Для этого выбирают такую случайную величину 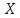 , математическое ожидание которой равно a: , математическое ожидание которой равно a: 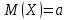 [Соболь 1973: 8]. [Соболь 1973: 8].Практически же поступают так: производят nиспытаний, в результате которых получают nвозможных значений 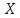 ; вычисляют их среднее арифметическое ; вычисляют их среднее арифметическое 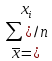 , принимают xв качестве оценки (приближенного значения) , принимают xв качестве оценки (приближенного значения) 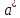 искомого числа a: искомого числа a: 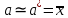 . Теория метода Монте – Карло указывает, как наиболее целесообразно выбрать случайную величину X и как найти ее возможные значения [Гмурман 2003: 364]. . Теория метода Монте – Карло указывает, как наиболее целесообразно выбрать случайную величину X и как найти ее возможные значения [Гмурман 2003: 364]. Стоит отметить достоинства метода Монте – Карло, которые являются его особенностями: Простая структура вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания. Затем это испытание повторяется N раз, и каждый опыт не зависит от всех остальных, а результаты всех опытов усредняются. Погрешность вычислений, пропорциональна 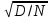 , где D – некоторая постоянная, N – число испытаний. Отсюда видно, что для того, чтобы уменьшить погрешность в 10 раз, нужно увеличить N в 100 раз. Таким путем добиться высокой точности невозможно. Поэтому обычно говорят, что метод Монте – Карло эффективен при решении тех задач, в которых результат нужен с небольшой точностью в пределах 0.01 (а может быть и выше в некоторых случаях) или вернее для оценки чего-либо. , где D – некоторая постоянная, N – число испытаний. Отсюда видно, что для того, чтобы уменьшить погрешность в 10 раз, нужно увеличить N в 100 раз. Таким путем добиться высокой точности невозможно. Поэтому обычно говорят, что метод Монте – Карло эффективен при решении тех задач, в которых результат нужен с небольшой точностью в пределах 0.01 (а может быть и выше в некоторых случаях) или вернее для оценки чего-либо.1.3. Генераторы случайных чиселДля решения задач с использованием метода Монте – Карло необходимы случайные числа. В качестве основной совокупности случайных чисел, используемых для получения других случайных элементов, выбирается последовательность, которая может быть получена с минимальными затратами машинного времени, и кроме того, обеспечивает удобство и простоту преобразований. Таким требованиям соответствует совокупность случайных чисел с равномерным распределением в интервале (0, 1). Основные свойства равномерного распределения. Непрерывная случайная величина имеет равномерное распределение в интервале (a, b), если ее функция плотности равна: 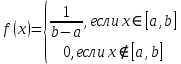 Математическое ожидание и дисперсия соответственно равны: 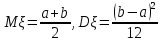 1.4. Интегрирование методом Монте – КарлоГеометрическое описание интеграла от некоторой функции 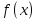 , есть площадь криволинейной трапеции под графиком этой функции, ограниченная сегментом , есть площадь криволинейной трапеции под графиком этой функции, ограниченная сегментом 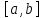 оси Ox и вертикальными прямыми проведенными через точки оси Ox и вертикальными прямыми проведенными через точки 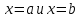 . Поэтому нахождение интеграла функции . Поэтому нахождение интеграла функции 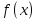 равного равного 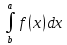 , можно рассматривать как нахождение криволинейной трапеции, ограниченной графиком функции , можно рассматривать как нахождение криволинейной трапеции, ограниченной графиком функции 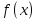 , осью , осью 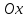 и прямыми и прямыми 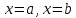 . . 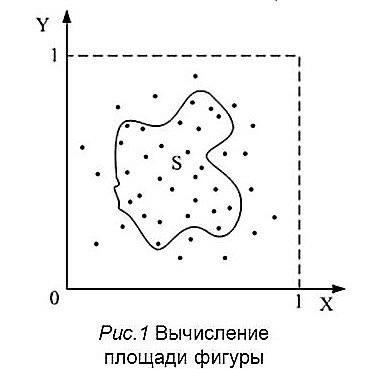 Предположим, что нам нужно вычислить площадь плоской фигуры S. Это может быть совсем произвольная фигура с криволинейной границей, заданная графически или аналитически, связанная или состоящая из нескольких кусков. Предположим, что нам нужно вычислить площадь плоской фигуры S. Это может быть совсем произвольная фигура с криволинейной границей, заданная графически или аналитически, связанная или состоящая из нескольких кусков. Рис. 1 Пусть это будет фигура, изображённая на рис.1, и предположим, что она расположена внутри единичного квадрата. Выберем в квадрате 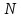 случайных точек. Обозначим через случайных точек. Обозначим через 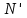 число точек, попавших при этом внутрь S. Геометрически очевидно, что площадь S приближённо равна отношению число точек, попавших при этом внутрь S. Геометрически очевидно, что площадь S приближённо равна отношению 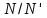 . .Причём, чем больше будет 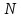 , тем больше будет точность этой оценки. Однако при таком опыте не все , тем больше будет точность этой оценки. Однако при таком опыте не все 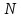 точек будут попадать в фигуру S. Возможно и такое, что значение точек будут попадать в фигуру S. Возможно и такое, что значение 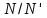 будет больше значения площади. Поэтому стоит уточнить, что данный метод вычисления справедлив только тогда, когда случайные точки будут не “просто случайными”, но и “равномерно распределенными” по всему квадрату, т.е. при таком подходе следует использовать равномерные случайные величины. будет больше значения площади. Поэтому стоит уточнить, что данный метод вычисления справедлив только тогда, когда случайные точки будут не “просто случайными”, но и “равномерно распределенными” по всему квадрату, т.е. при таком подходе следует использовать равномерные случайные величины.В общем случае, если площадь квадрата (или любой другой фигуры площадь которой известна) равна 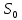 и в результате и в результате 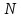 испытаний, из которых при испытаний, из которых при 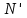 исходах случайные точки оказались внутри фигуры, тогда площадь фигуры будет определяться выражением: исходах случайные точки оказались внутри фигуры, тогда площадь фигуры будет определяться выражением: 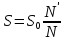 Такой подход к вычислению определенного интеграла называют стохастическим алгоритмом, основанном на истолковании интеграла как площади Способ основанный на истолковании интеграла как площади Пусть подынтегральная функция неотрицательна и ограничена: 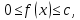 а случайная величина (X,Y) распределена равномерно в прямоугольнике D с основанием а случайная величина (X,Y) распределена равномерно в прямоугольнике D с основанием 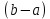 и высотой и высотой 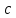 . Тогда в качестве оценки интеграла . Тогда в качестве оценки интеграла 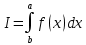 принимают принимают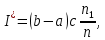 где 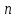 – общее число случайных точек – общее число случайных точек 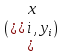 , принадлежащих D; , принадлежащих D; 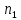 – число случайных точек, которые расположены под кривой – число случайных точек, которые расположены под кривой 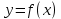 [Гмурман 2004: 319]. [Гмурман 2004: 319]. Способ усреднения подынтегральной функции  В качестве оценки определенного интеграла 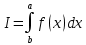 принимают принимают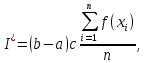 где 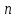 – число испытаний; – число испытаний; 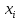 – возможные значения случайной величины – возможные значения случайной величины 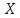 , распределенной в интервале , распределенной в интервале 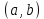 , их разыгрывают по формуле , их разыгрывают по формуле 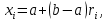 где где 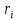 – случайной число [Гмурман 2004: 317]. – случайной число [Гмурман 2004: 317].ГЛАВА 2. ПРАКТИЧЕСКАЯ ЧАСТЬРассмотрим применение метода Монте-Карло для решения некоторых задач, имеющих прикладной характер.   Пример. Тело движется прямолинейно со скоростью 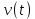 (м/c). Найдите путь, пройденный за промежуток времени от (м/c). Найдите путь, пройденный за промежуток времени от 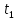 до до 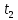 , если скорость изменяется по закону, выраженному следующей формулой , если скорость изменяется по закону, выраженному следующей формулой 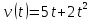 , а , а 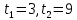 Решение: Из курса физики известно, что пройденный путь можно представить, как определенный интеграл от модуля скорости по времени. 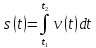 Тогда: 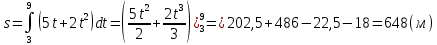 Полученный результат, является точным значением. Получим значение определенного интеграла с помощью метода статистических испытаний с применением стохастического алгоритма. Определим область, в рассматриваемой задаче это прямоугольник 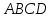 , со сторонами , со сторонами 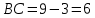 и и 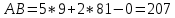 ограничивающий функцию ограничивающий функцию 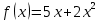 . Генерируем последовательность равномерно распределенных в прямоугольнике . Генерируем последовательность равномерно распределенных в прямоугольнике 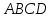 случайных величин, т.е. случайных величин, т.е. 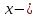 равномерно распределена на отрезке равномерно распределена на отрезке 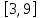 , , 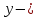 на отрезке на отрезке 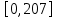 . .Находим значение интеграла по формуле: 
Приведем графическое изображение распределения случайных точек: 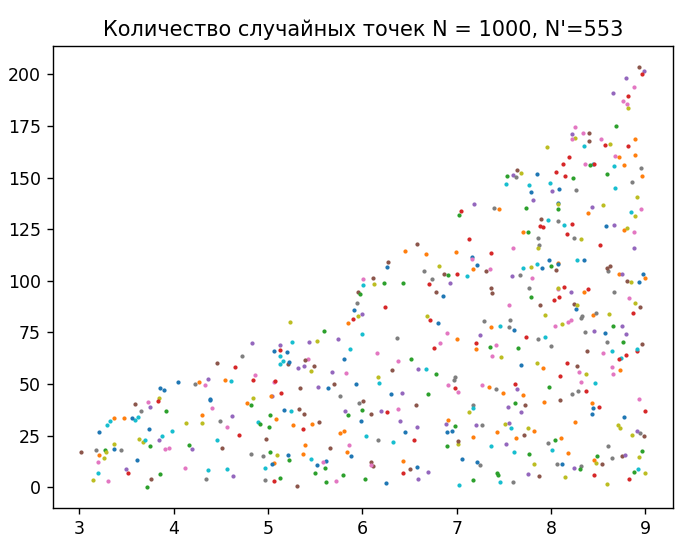 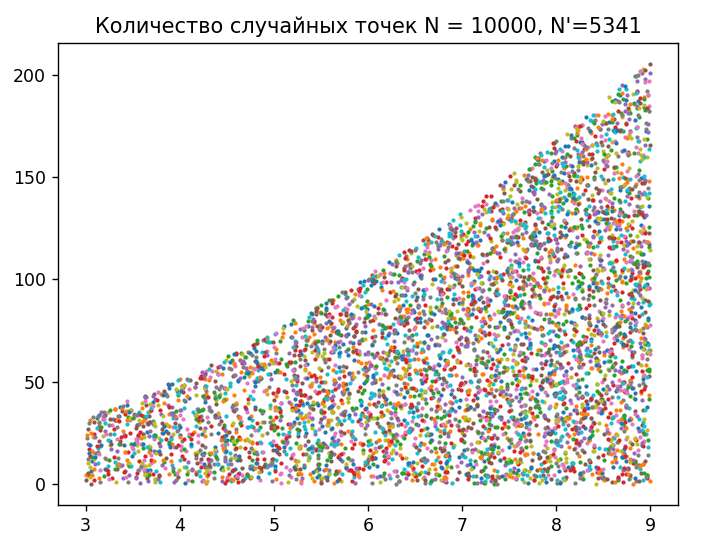 Теперь попробуем получить значение способом усреднения подынтегральной функции:
Найдем 100 значений интеграла для каждого набора 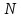 случайных чисел и вычислим для каждого из значений абсолютную погрешность. Используем полученные данные для нахождения статистических погрешностей. случайных чисел и вычислим для каждого из значений абсолютную погрешность. Используем полученные данные для нахождения статистических погрешностей.Таблица статистических погрешностей, для полученных значений:
Проанализировав данные таблицы статистических погрешностей, можем сделать вывод о том, что способ усреднения подынтегральной функции обладает меньшей погрешностью. Воспользуемся полученным выводом и рассмотрим применение метода Монте – Карло для нахождения некоторых “неберущихся” интегралов, имеющих важное прикладное значение. Один из самых известных первообразных является функция Лапласа: 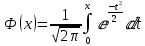 Функция Лапласа широко применяется в теории вероятностей, математической и прикладной статистике и др. разделах науки и её приложений. Для вычисления ее значений составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Для нахождения определенного интеграла Лапласа, будем фиксировать значения 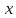 и вычислять значения функции и вычислять значения функции 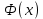 , и сравним их с истинными значениями из известных таблиц: , и сравним их с истинными значениями из известных таблиц:
ЗАКЛЮЧЕНИЕВ ходе исследовательской работы были изучены основы методы Монте – Карло, некоторые сведения из теории вероятности и математической статистики позволяющие вычислять значения определенного интеграла, даже если он является “неберущимся”. Написаны реализации двух методов (метода основанного на истолковании интеграла как площади и метода усреднения подынтегральной функции) на языке Python, представлены их коды, а также проведены сравнения между двумя методами. В ходе работы был приведен пример прикладной задачи, которую можно решить с использованием мтеода статистических испытаний. Из приведенной таблицы для оценки погрешностей можно сделать вывод, что статистическая погрешность убывает медленно (при увеличении количества случайных точек в 10 раз, погрешность уменьшается в 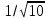 ), а также, что метод усреднения подынтегральной функции даёт результат с наименьшей погрешностью. ), а также, что метод усреднения подынтегральной функции даёт результат с наименьшей погрешностью. Нахождение значений “неберущегося” интеграла Лапласа, без каких-либо аналитических вычислений, наглядно продемонстрировало полезность применимости метода Монте –Карло, который является универсальным аппаратом для решения многих других прикладных задач. СПИСОК ЛИТЕРАТУРЫ1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (3 – е изд.). М.: Высш. шк., 1979, – 400 с. 2. Гмурман В.Е. Теория вероятностей и математическая статистика (9 – е изд.). М.: Высшая школа, 2003. – 479 с. 3. Ермаков С.М. Метод Монте – Карло и смежные вопросы – М.: Наука, 1975 – 472 с. 4. Соболь И.М. Метод Монте – Карло – М.: Наука, 1985. – 80 c. 5. Соболь И. M. Численные методы Монте-Карло. — М.: Главная редакция физико-математической литературы издательства «Наука», 1973. — 312 с. ПРИЛОЖЕНИЕПрограмма 1.import random import matplotlib.pyplot as plt print('y <= (5x + 2x^2)') N = 10**4 k = 0 ist = 648 sp = [] s = 0 for i in range(N): x = random.uniform(3, 9) y = random.uniform(0, 207) if y <= (5*x + 2*x*x): k+=1 plt.scatter(x,y, s=2) s = 207 * 6 * k / N plt.title(f"Количество случайных точек N = {N}, N'={k}") plt.show() print('I = ', s) Программа 2.import random a = 3 b = 9 N = 10**5 k = b - a s1 = 0 s1 = 0 for i in range(N): x = random.uniform(a, b) s1 += (5*x + 2*x*x) print('I = ', round((s1/N)*k, 3)) Программа 3.import random from math import pi, exp, sqrt a = 0 b = 2.48 N = 10**6 k = b - a s1 = 0 sp = [] for ex in range(10): s1 = 0 for i in range(N): x = random.uniform(a, b) s1 += exp(-(x**2)/2) sq = (s1*k)/N sp.append(sq/(sqrt(2*pi))) print(sq/(sqrt(2*pi))) print(sum(sp)/10) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||