Контрольная работа по математике. КР номер 2. Даны координаты вершин треугольника А(3 4), В(1 2) и С(2 1)
 Скачать 193.31 Kb. Скачать 193.31 Kb.
|
|
Даны координаты вершин треугольника А(3; 4), В(-1; 2) и С(2; -1). Запишите общее уравнение средней линии треугольника, параллельной ВС. Решение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. В данной задаче это стороны АВ и АС. Пусть серединой АВ является точка М, а серединой АС - точка К. Тогда их координаты определяются по формулам: 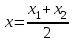 ; ;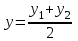 ; ;Получаем: М(1; 3), К(2, 5;1, 5). Необходимо найти уравнение прямой, проходящей через эти точки. Отрезок МК параллелен вектору МК(1, 5;-1, 5) и перпендикулярен вектору N(1; 1), который можно принять в качестве вектора нормали отрезка МК. Общее уравнение прямой имеет вид: Ax + By + C = 0, где C = - Ax0 - By0 Здесь коэффициенты А, В определяют координаты вектора N, x0, y0 - координаты одной из точек, лежащих на отрезке МК. Примем x0, y0 за координаты точки К запишем искомое уравнение: x + y - (2,5 + 1,5) = 0, или x + y - 4 = 0 Ответ: x + y - 4 = 0; 2. В прямоугольном треугольнике АВС известны: уравнение медианы 3x - 4y + 8 = 0, проведенной из вершины А(0; 2) прямого угла, и вершина В(2; 1). Найти координаты (x0, y0) вершины С треугольника. Решение. По условию задачи точка С имеет координаты х0, у0, то координаты точки М, - середины отрезка ВС, определяются по формулам. Находим: М( 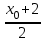 ; ;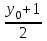 ). Для отыскания координат точки С составим систему из двух уравнений. Первое - для прямой АС, второе - для медианы АМ. Точка С лежит на прямой АС, которой перпендикулярен вектор АВ(2; -1). Поэтому уравнение для АС можно записать в виде 2x - y - (2*0 – 1*2) = 0, 2x - y + 2 = 0. В уравнение АМ для медианы подставим значения координат точки М, выраженные через координаты точек В и С. Получаем систему: ). Для отыскания координат точки С составим систему из двух уравнений. Первое - для прямой АС, второе - для медианы АМ. Точка С лежит на прямой АС, которой перпендикулярен вектор АВ(2; -1). Поэтому уравнение для АС можно записать в виде 2x - y - (2*0 – 1*2) = 0, 2x - y + 2 = 0. В уравнение АМ для медианы подставим значения координат точки М, выраженные через координаты точек В и С. Получаем систему: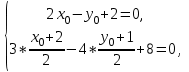 или или 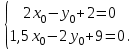 Отсюда находим: х0 = 2, у0 = 6. Ответ:__С(2;_6)._3._Запишите_общее_уравнение_плоскости,_проходящей_через_точки_М'>Ответ: С(2; 6). 3. Запишите общее уравнение плоскости, проходящей через точки М1(7; 2; -3) и М2(5; 6; -4) параллельно оси ОY. Решение. Данная плоскость параллельна векторам l1 = М1М2 = (-2; 4; -1) и l2 = (0; 1; 0) = j, поэтому ее вектор нормали 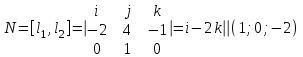 Записываем уравнение плоскости: х - 2z + D = 0. Т.к. плоскость проходит через точку М(7; 2; -3), то 7 + 6 + D = 0, отсюда D = -13. Ответ: x - 2z - 13 = 0; 4. Найдите коэффициент В в уравнении плоскости x + By + Cz + D = 0, проходящей через точки Р(1; -1; 1), О(0; 0; 0) параллельно прямой 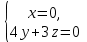 Решение. Данные прямая и плоскость могут быть параллельны только в том случае, если нормальк плоскости будет перпендикулярна направляющему вектору прямой. Нормаль к плоскости есть вектор N(1; В; С). Направляющий вектор l прямой можно найти из параметрического уравнения: 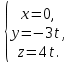 Следовательно, l(0; -3; 4), а [N, l] = -3В + 4С + D = 0, где D = 0. Уравнение плоскости выразим через коэффициенты В и С, подставив вместо x, y и z координаты точки Р(1; -1; 1). Получим: 1 - В + С =0. Составляем систему и находим искомые коэффициенты: 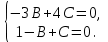 Отсюда В = 4, С = 3. Ответ: В = 4. 5. При каких значениях параметров А1 и А2 прямые 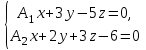 и и 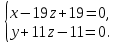 параллельны. Ответ запишите в виде пары чисел (А1, А2). Решение. Две прямые могут быть параллельны в том случае, если параллельны их направляющие векторы l1 и l2, т.е. когда их координаты пропорциональны. Направляющие векторы данных прямых можно найти как векторное произведение нормалей к заданным плоскостям. Для первой прямой получаем: N1 = (А1; 3; -5), N2 = (А2; 2; 3), а их векторное произведение: 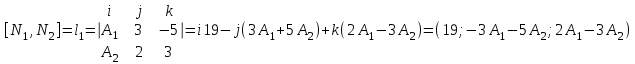 Для второй прямой: N3 = (1;0;-19), N4 = (0;1;11), а их векторное произведение: 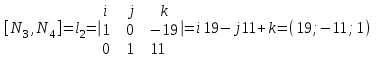 Составляем пропорцию: 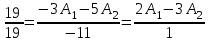 , отсюда видно, что коэффициент пропорциональности равен 1, составим систему и найдем искомые параметры: , отсюда видно, что коэффициент пропорциональности равен 1, составим систему и найдем искомые параметры: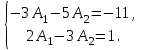 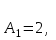 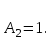 Ответ найден и можно выполнить проверку. Подставим найденные параметры в исходное уравнение, найдем координаты направляющих векторов для обеих прямых: l1 = (19; -1; 11), l2 = (19; -1; 11). Их координаты пропорциональны, следовательно, l1 || l2, а значит параллельны и прямые этих векторов. Параметры найдены верно. Ответ:_А'>Ответ: А1 = 2, А2 = 1. 6. Найдите длину отрезка, отсекаемого от оси аппликат плоскостью, содержащей прямую 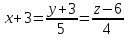 и отсекающей на осях абсцисс и ординат одинаковой длины отрезки. и отсекающей на осях абсцисс и ординат одинаковой длины отрезки.Решение. Известно, что общее уравнение плоскости имеет вид Ах + Ву + Cz + D = 0. В данной задаче предполагается, что D ≠ 0, т.к. по условию плоскость не проходит через начало координат. В точке пересечения плоскости с осью Ох координаты y и z обращаются в нуль. Тогда в этой точке уравнение плоскости имеет вид Ax + D = 0, отсюда 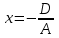 . При пересечении плоскости с осью Oy координаты x и z обращаются в нуль, и тогда уравнение плоскости принимает вид By + D = 0, . При пересечении плоскости с осью Oy координаты x и z обращаются в нуль, и тогда уравнение плоскости принимает вид By + D = 0, 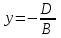 . Т.к. по условию |x| = |y|, то . Т.к. по условию |x| = |y|, то 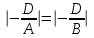 , причем А ≠ 0, В ≠ 0. Отсюда |A| = |B| (при D ≠ 0). Из последнего равенства следует, что А = В, и А = -В. , причем А ≠ 0, В ≠ 0. Отсюда |A| = |B| (при D ≠ 0). Из последнего равенства следует, что А = В, и А = -В.Т.к. плоскость содержит прямую 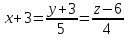 , то все точки, лежащие на этой прямой, удовлетворяют и данной плоскости. Найдем две такие точки. М1(-3; -3; 6) и М2(-2; 2; 10). Подставляя координаты точек в общее уравнение плоскости, получим еще два уравнения для нахождения коэффициентов А, В и С: -3A - 3B + 6C + D = 0, и -2A + 2B +10C + D = 0. Учитывая, что А = В и А = -В (по определению модуля), получим две системы уравнений: , то все точки, лежащие на этой прямой, удовлетворяют и данной плоскости. Найдем две такие точки. М1(-3; -3; 6) и М2(-2; 2; 10). Подставляя координаты точек в общее уравнение плоскости, получим еще два уравнения для нахождения коэффициентов А, В и С: -3A - 3B + 6C + D = 0, и -2A + 2B +10C + D = 0. Учитывая, что А = В и А = -В (по определению модуля), получим две системы уравнений: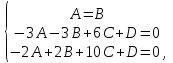 и и 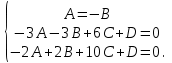 Решая первую систему относительно А, В и С, получаем: 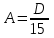 , ,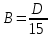 , ,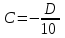 . Подставляя найденные значения коэффициентов в общее уравнение плоскости, получим: . Подставляя найденные значения коэффициентов в общее уравнение плоскости, получим: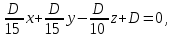 x + y - 1,5z + 15 = 0. x + y - 1,5z + 15 = 0.В качестве проверки можно найти скалярное произведение вектора нормали N(1;1;-1,5) этой плоскости и направляющего вектора l (1;5;4) прямой. Если уравнение найдено верно, то (N,l) = 0. Проверим: 1ּ1 + 1ּ5 + (-1,5)ּ4 = 0. Уравнение найдено верно. Данная плоскость пересекает ось Oz в точке (0;0;10), т.е. длина отрезка, отсекаемого плоскостью на оси Oz равна 10. Решая вторую систему относительно А, В и С, получаем: А = 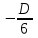 , В = , В = 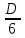 , C = , C = 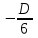 . Подставим найденные коэффициенты и найдем искомое уравнение: . Подставим найденные коэффициенты и найдем искомое уравнение: x - y + z - 6 = 0. x - y + z - 6 = 0.Проверка: (N,l) = 1*1 + (-1)*5 + 1*4 = 0. Уравнение найдено верно. Длина отрезка, отсекаемого плоскостью на оси Oz равна 6. Ответ: z = 10, либо z = 6. 7. Найдите уравнение касательной плоскости к сфере x2 + y2 + z2 - 8x + 6y + 4z - 12 = 0 в точке М0(1; 1; 2). Решение. Положение плоскости в пространстве определяется заданием ее вектора нормали и какой-нибудь точки, лежащей в этой плоскости. За вектор нормали примем СМ0, где точка С - центр сферы, М0 (1;1;2). Выделим полные квадраты уравнения: (x - 4)2 + (y + 3)2 + (z + 2)2 = 12 + 16 + 9 + 4, (x - 4)2 + (y + 3)2 + (z + 2)2 = 41. Следовательно, С (4;-3;-2), тогда СМ0 (-3;4;4). Поэтому искомое уравнение имеет вид: -3x + 4y + 4z - ((-3)*1+4*1+4*2) = 0, -3x + 4y + 4z - 9 = 0. Ответ: -3x + 4y + 4z - 9 = 0. 8. Дана кривая 4x2 - 32x - y2 +6y + 51 = 0. 8.1. Доказать, что эта кривая - гипербола. 8.2. Найти координаты ее центра симметрии. 8.3. Найти действительную и мнимую полуоси. 8.4. Записать уравнение фокальной оси. 8.5. Построить данную гиперболу. Решение. 8.1. Известно, что каноническое уравнение гиперболы имеет вид:  . Преобразуем уравнение 4x2 - 32x - y2 +6y + 51 = 0, выделив полные квадраты: 4(х - 4)2 - (у - 3)2 = 4, или . Преобразуем уравнение 4x2 - 32x - y2 +6y + 51 = 0, выделив полные квадраты: 4(х - 4)2 - (у - 3)2 = 4, или  . Положим х1 = (х - 4), у1 = (у - 3), тогда . Положим х1 = (х - 4), у1 = (у - 3), тогда  . Данное уравнение определяет гиперболу. . Данное уравнение определяет гиперболу.8.2. Решая систему уравнений х1 = 0 и у1 = 0, находим центр симметрии - точку О1 с координатами (4;3). 8.3. Из канонического уравнения гиперболы, найденного в п.8.1., видно, что действительная полуось  мнимая мнимая  8.4. В новой системе координат оси направлены по прямым х - 4 = 0 (ось ОY1) и у - 3 = 0 (ось ОХ1), которая и является фокальной осью. 8.5. Для построения более точного графика найдем асимптоты данной гиперболы и точки ее пересечения со старыми осями координат. Известно, что асимптотами гиперболы являются прямые  . Из этого соотношения находим уравнения асимптот: . Из этого соотношения находим уравнения асимптот:  Кривая пересекает ось ОХ в точках (2, 2; 0) и (5, 8; 0), ось ОY - в точках (0; -4, 7) и (0; 10, 7). Строим данную гиперболу.  9. Дана кривая 4x + 6y - y2 = 21. 9.1. Доказать, что данная кривая - парабола. 9.2. Найти координаты ее вершины. 9.3. Найти значение ее параметра p. 9.4. Записать уравнение ее оси симметрии. 9.5. Построить данную параболу. Решение. 9.1. Каноническое уравнение параболы имеет вид: у2 = 2рх. Преобразуем уравнение 4x + 6y - y2 = 21, выделив полные квадраты: (у - 3)2 = 4(х - 3). Положим у1 = у - 3, х1 = х - 3, тогда уравнение приводится к виду  = 4х1. Данное уравнение определяет параболу. = 4х1. Данное уравнение определяет параболу.9.2. Решая систему уравнений у1 = 0 и х1 = 0, находим вершину параболы - точку О1 с координатами (3;3). 9.3. Из канонического уравнения параболы, найденного в п.9.1., видно, что 2р = 4, р = 2. 9.4. В новой системе координат оси направлены по прямым х - 3 = 0 (ось ОY1) и у - 3 = 0 (ось ОХ1), которая и является осью симметрии данной параболы. 9.5. Для построения более точного графика найдем точки пересечения данной кривой со старыми осями координат. Кривая пересекает только ось ОХ в точке (5, 25; 0). Строим кривую.  10. Дана кривая 5x2 + 5y2 + 8xy - 18x - 18y + 9 = 0. 10.1. Доказать, что эта кривая - эллипс. 10.2. Найти координаты его центра симметрии. 10.3. Найти большую и малую полуоси. 10.4. Записать уравнение фокальной оси. 10.5. Построить данную кривую. Решение. 10.1. Квадратичную форму В (х,у) = 5х2 + 5у2 + 8ху приводим к главным осям. Для этого записываем матрицу этой формы В =  и находим ее собственные числа и собственные векторы. Составим и решим характеристическое уравнение этой матрицы: и находим ее собственные числа и собственные векторы. Составим и решим характеристическое уравнение этой матрицы: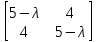 = 0, (5 - λ)2 - 16 = 0. = 0, (5 - λ)2 - 16 = 0.Его корни λ1 = 1, λ2 = 9 являются собственными числами. Т.к. λ1 · λ2 > 0, то кривая 5x2 + 5y2 + 8xy - 18x - 18y + 9 = 0 - эллипс. 10.2. Координаты собственного вектора, отвечающего числу λ1 = 1, удовлетворяют соотношению ξ1 = -ξ2. В качестве нового базисного вектора примем вектор i1 = 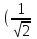 ;- ;-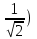 . Другой базисный вектор j1 = . Другой базисный вектор j1 = 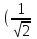 ; ;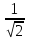 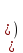 . Записываем матрицу Q перехода от базиса O, i, j к базису O, i1, j1: . Записываем матрицу Q перехода от базиса O, i, j к базису O, i1, j1: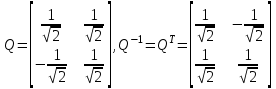 . .По формуле перехода от одного базиса к другому выражаем старые координаты х и у через новые х1 и у1: 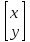 = = 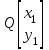 , , 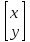 = = 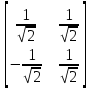 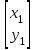 , отсюда x = , отсюда x = 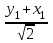 , y = , y = 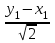 . .Уравнение 5x2 + 5y2 + 8xy - 18x - 18y + 9 = 0 в новой системе координат примет вид: 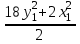 - - 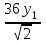 = -9, или = -9, или  Произведем параллельный перенос системы координат в новое начало О1 по формулам: x2 = x1,  х1 и у1 найдем по формулам:  = Q-1 = Q-1  , , 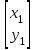 = = 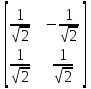 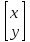 . .x1 = 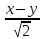 , y1 = , y1 =  ; ;x2 =  , y2 = , y2 =  . .Решая систему уравнений х2 = 0 и у2 = 0, найдем координаты нового начала О1(1; 1). Точка О1(1; 1) - центр симметрии эллипса. 10.3. Уравнение (10.2) приводим к каноническому уравнению эллипса:  + + = 1. Отсюда большая полуось а = = 1. Отсюда большая полуось а =  = 3, малая b = = 3, малая b =  = 1. = 1.10.4. В новой системе координат оси направлены по прямым у = х (ось О1Y2) и у = - х + 2 (ось O1X2), которая и является фокальной осью эллипса. 10.5. Для построения более точного графика найдем дополнительные точки кривой эллипса. Например, точки пересечения со старыми осями координат. Ось OY кривая пересекает в точках (0; 0, 6) и (0; 3); ось OX - в точках (0, 6; 0) и (3; 0). Строим данную кривую.  |
