Экзамен_тесты_2021_для_студентов. экзаменационный билет 1 по дисциплине Эконометрика

• Название: экзаменационный билет 1 по дисциплине Эконометрика
• Дата: 29.03.2023
• Размер: 467.37 Kb.
• Имя файла: Экзамен_тесты_2021_для_студентов.doc
• Тип: Документы; #1023131

[ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1

по дисциплине «Эконометрика»

1 При умножении случайной величины на константу, математическое ожидание умножается.

А) на эту же константу;

В) на квадрат этой константы;

C) на ½ этой константы;

D) на ¼ этой константы;

Е) на (-1).

2 Дисперсия случайной величины определяется как:

А) квадрат разности между значением случайной величины и ее математическим ожиданием;

В) математическое ожидание разности между значением случайной величины и ее математическим ожиданием;

C) математическое ожидание квадрата разности между значением случайной величины и ее математическим ожиданием;

D) математическое ожидание от квадрата отклонения;

Е) математическое ожидание от куба отклонения случайной величины от ее математического ожидания.
3 Дан закон распределения . Найти:

	1	2	3	4
	0.3	0.1	0.2	0.4

4 Непрерывная случайная величина задана следующей функцией распределения: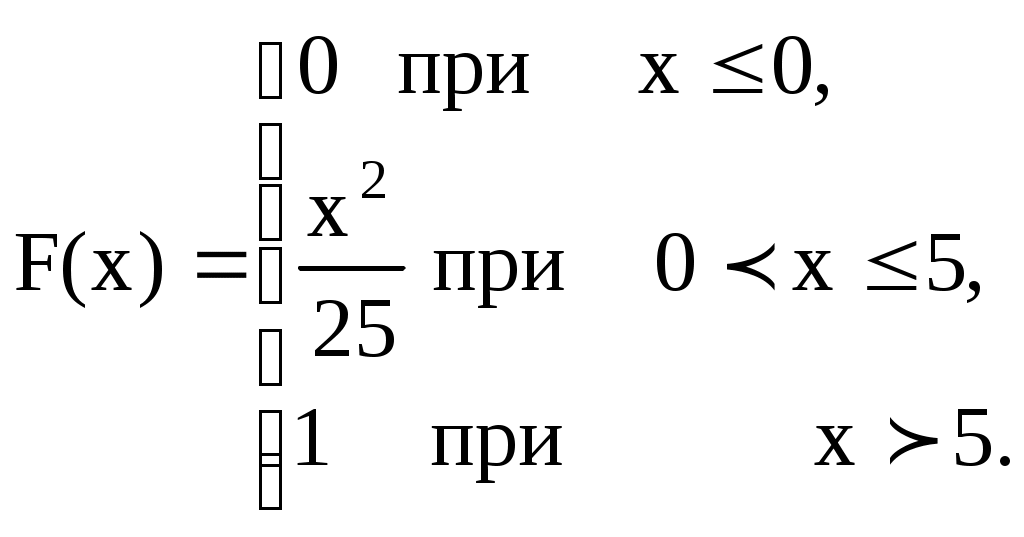

Найти математическое ожидание случайной величины .

5 Дано статистическое распределение выборки:



Найти выборочную среднюю.

6 Найти дисперсию случайной величины , если и несовместные

7 Выполнимость условий для любых наблюдений называется

A) гомоскедастичностью;

B) гетероскедастичностью;

C) автокорреляцией;

D) мультиколлинеарностью;

E) автокоррелцией первого рода.

8 Чем теснее линейная связь между X и Y, тем ближе коэффициент детерминации к :

A) 1;

B) 0;

C) -1;

D) ;

E) 2.

9 Дана таблица наблюдений Найти коэффициент в уравнений регрессии

	1	2	3
	2	3	4

10 Предположение о величине параметра распределения генеральной совокупности называется

A) статистической гипотезой;

B) математическим ожиданием;

C) средним квадратическим отклонением;

D) гетероскедастичностью;

E) автокорреляцией.

11 При проверке нулевой гипотезы ( ) было получено следующее значение - статистики коэффициента парной линейной регрессии Определите коэффициент , если его стандартная ошибка равна 0.001:

A) =2400;

B) =0.0024;

C) =0.024;

D) =2.4;

E) =0.24.

12 Найти , учитывая, что =15,

13 Для четырех пар наблюдений имеются следующие результаты:



Найти коэффициент детерминации
14 Какой вид будет иметь уравнение парной линейной регрессии переменных и если известно, что их средние значения равны соответственно 18 и 4.75, а коэффициент равен 2;

15 Если Х неслучайная величина, то условие Гаусса-Маркова, предполагающее, что случайный член должен быть распределен независимо от объясняющих переменных может быть представлено в виде:

A) ;

B) ;

C) ;

D) ;

E)

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2

по дисциплине «Эконометрика»
1 При умножении случайной величины на константу, дисперсия умножается.

А) на эту же константу;

В) на квадрат этой константы;

C) на ½ этой константы;

D) на ¼ этой константы;

Е) на (-1).

2 Дано статистическое распределение выборки

	1	3	4	6	8
	3	2	1	5	4

Найти среднее выборочное:

3 Дан закон распределения

	1	2	3	4
	0.3	0.1	0.2	0.4

Найти:

4 Найти математическое ожидание случайной величины , если известны математические ожидания .

5 Найти , учитывая, что =25,

6 При переходе к условным вариантам выборочная средняя будет равна:

A) ;

B) ;

C) ;

D) ;

E) .

7 При переходе к условным вариантам выборочная дисперсия будет равна:

A) ;

B) ;

C) ;

D) ;

E) .

8 По выборке объема найдена смещенная оценка генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.

9 Условие независимости случайных отклонений и друг от друга для требует:

А) закон больших чисел;

В) центральная предельная теорема;

C) теорема Чебышева;

D) теорема Гаусса-Маркова;

Е) теорема Бернулли

10 Уровнем значимости называется:

A) Вероятность совершить ошибку первого рода;

B) Вероятность совершить ошибку второго рода;

C) Вероятность не совершить ошибку первого рода;

D) Вероятность отклонения случайной величины от ее математического ожидания;

E) Вероятность не совершить ошибку второго рода.

11 Суть МНК состоит в:

A) минимизации суммы квадратов коэффициентов регрессии;

B) минимизации суммы квадратов значений зависимой переменной;

C) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии;

D) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии;

E) максимизации суммы квадратов коэффициентов регрессии.
12 Для четырех пар наблюдений имеются следующие результаты:



Найти коэффициент детерминации

13 Какой вид имеет уравнение парной линейной регрессии переменных и , если известно, что их средние значения равны 30.5 и 5.75,

14 При проверке нулевой гипотезы , было получено следующее значения статистики . Определить коэффициент , если его стандартная ошибка равна 0.001.

A) 0.025;

B) 0.026;

C) 0.36;

D) 0.036;

E) 0.56.

15 Определить параметр парной линейной регрессии, оцененной по 30 наблюдениям, если известно

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3

по дисциплине «Эконометрика»


1. Дан закон распределения . Найти:

	1	2	3	5
	0.3	0.1	0.2	0.4

2. 
   Непрерывная случайная величина задана следующей функцией распределения: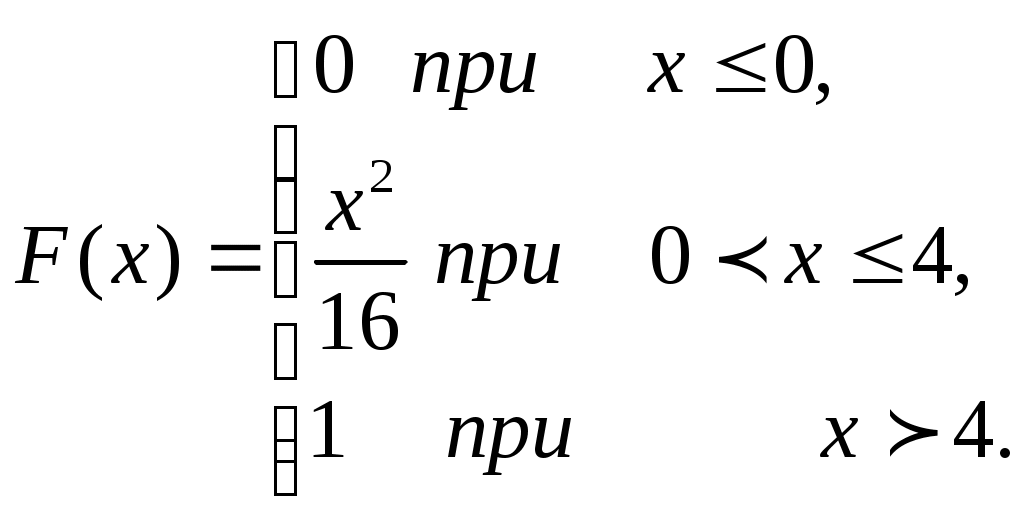
   

Найти математическое ожидание случайной величины .

3. Дано статистическое распределение выборки:



Найти выборочную среднюю.

4.При умножении случайной величины на константу, математическое ожидание умножается.

А) на эту же константу;

В) на квадрат этой константы;

C) на ½ этой константы;

D) на ¼ этой константы;

Е) на (-1).

5. 
   Дисперсия случайной величины определяется как:
   

А) квадрат разности между значением случайной величины и ее математическим ожиданием;

В) математическое ожидание разности между значением случайной величины и ее математическим ожиданием;

C) математическое ожидание квадрата разности между значением случайной величины и ее математическим ожиданием;

D) математическое ожидание от квадрата отклонения;

Е) математическое ожидание от куба отклонения случайной величины от ее математического ожидания.
6. Найти дисперсию случайной величины , если и несовместные

7. Выполнимость условий для любых наблюдений называется

A) гомоскедастичностью;

B) гетероскедастичностью;

C) автокорреляцией;

D) мультиколлинеарностью;

E) автокоррелцией первого рода.

8. Чем теснее линейная связь между X и Y, тем ближе коэффициент детерминации к :

A) 1;

B) 0;

C) -1;

D) ;

E) 2.

9. Дана таблица наблюдений Найти коэффициент в уравнений регрессии

	1	2	3
	2	4	5

10. Предположение о величине параметра распределения генеральной совокупности называется

A) статистической гипотезой;

B) математическим ожиданием;

C) средним квадратическим отклонением;

D) гетероскедастичностью;

E) автокорреляцией.

11. При проверке нулевой гипотезы ( ) было получено следующее значение - статистики коэффициента парной линейной регрессии Определите коэффициент , если его стандартная ошибка равна 0.001:

A) =2500;

B) =0.0025;

C) =0.025;

D) =2.5;

E) =0.25.

12. Найти , учитывая, что =15,

13. Для четырех пар наблюдений имеются следующие результаты:



Найти коэффициент детерминации
14. Какой вид будет иметь уравнение парной линейной регрессии переменных и если известно, что их средние значения равны соответственно 18 и 4.75, а коэффициент равен 2;

15. Если Х неслучайная величина, то условие Гаусса-Маркова, предполагающее, что случайный член должен быть распределен независимо от объясняющих переменных может быть представлено в виде:

A) ;

B) ;

C) ;

D) ;

E)

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

по дисциплине «Эконометрика»
1 Найти математическое ожидание случайной величины , если известны математические ожидания .



2 Дано статистическое распределение выборки

	1	3	4	7	8
	3	2	1	5	4

Найти среднее выборочное:

3 Дан закон распределения

	1	2	3	4
	0.3	0.1	0.2	0.4

Найти:

4 При умножении случайной величины на константу, дисперсия умножается.

А) на эту же константу;

В) на квадрат этой константы;

C) на ½ этой константы;

D) на ¼ этой константы;

Е) на (-1).

5 Найти , учитывая, что =35,

6 При переходе к условным вариантам выборочная средняя будет равна:

A) ;

B) ;

C) ;

D) ;

E) .

7 При переходе к условным вариантам выборочная дисперсия будет равна:

A) ;

B) ;

C) ;

D) ;

E) .

8 По выборке объема найдена смещенная оценка генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.

9 Условие независимости случайных отклонений и друг от друга для требует:

А) закон больших чисел;

В) центральная предельная теорема;

C) теорема Чебышева;

D) теорема Гаусса-Маркова;

Е) теорема Бернулли

10 Уровнем значимости называется:

A) Вероятность совершить ошибку первого рода;

B) Вероятность совершить ошибку второго рода;

C) Вероятность не совершить ошибку первого рода;

D) Вероятность отклонения случайной величины от ее математического ожидания;

E) Вероятность не совершить ошибку второго рода.

11 Суть МНК состоит в:

A) минимизации суммы квадратов коэффициентов регрессии;

B) минимизации суммы квадратов значений зависимой переменной;

C) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии;

D) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии;

E) максимизации суммы квадратов коэффициентов регрессии.
12 Для четырех пар наблюдений имеются следующие результаты:



Найти коэффициент детерминации

13 Какой вид имеет уравнение парной линейной регрессии переменных и , если известно, что их средние значения равны 30.5 и 5.75,

14 При проверке нулевой гипотезы , было получено следующее значения статистики . Определить коэффициент , если его стандартная ошибка равна 0.001.
15 Определить параметр парной линейной регрессии, оцененной по 30 наблюдениям, если известно

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

по дисциплине «Эконометрика»

1. 
   При переходе к условным вариантам выборочная дисперсия будет равна:
   

A) ;

B) ;

C) ;

D) ;

E) .

2. 
   По выборке объема найдена смещенная оценка генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
   

3. 
   Условие независимости случайных отклонений и друг от друга для требует:
   

А) закон больших чисел;

В) центральная предельная теорема;

C) теорема Чебышева;

D) теорема Гаусса-Маркова;

Е) теорема Бернулли

4. Уровнем значимости называется:

A) Вероятность совершить ошибку первого рода;

B) Вероятность совершить ошибку второго рода;

C) Вероятность не совершить ошибку первого рода;

D) Вероятность отклонения случайной величины от ее математического ожидания;

E) Вероятность не совершить ошибку второго рода.

5. Суть МНК состоит в:

A) минимизации суммы квадратов коэффициентов регрессии;

B) минимизации суммы квадратов значений зависимой переменной;

C) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии;

D) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии;

E) максимизации суммы квадратов коэффициентов регрессии.
6. Для четырех пар наблюдений имеются следующие результаты:



Найти коэффициент детерминации
7. Какой вид имеет уравнение парной линейной регрессии переменных и , если известно, что их средние значения равны 30.5 и 5.75,
8. При проверке нулевой гипотезы , было получено следующее значения статистики . Определить коэффициент , если его стандартная ошибка равна 0.001.
9. Определить параметр парной линейной регрессии, оцененной по 30 наблюдениям, если известно

10. При умножении случайной величины на константу, математическое ожидание умножается.

А) на эту же константу;

В) на квадрат этой константы;

C) на ½ этой константы;

D) на ¼ этой константы;

Е) на (-1).

11. Дисперсия случайной величины определяется как:

А) квадрат разности между значением случайной величины и ее математическим ожиданием;

В) математическое ожидание разности между значением случайной величины и ее математическим ожиданием;

C) математическое ожидание квадрата разности между значением случайной величины и ее математическим ожиданием;

D) математическое ожидание от квадрата отклонения;

Е) математическое ожидание от куба отклонения случайной величины от ее математического ожидания.
12. Дан закон распределения . Найти:

	1	2	3	4
	0.3	0.2	0.1	0.4

13. Непрерывная случайная величина задана следующей функцией распределения: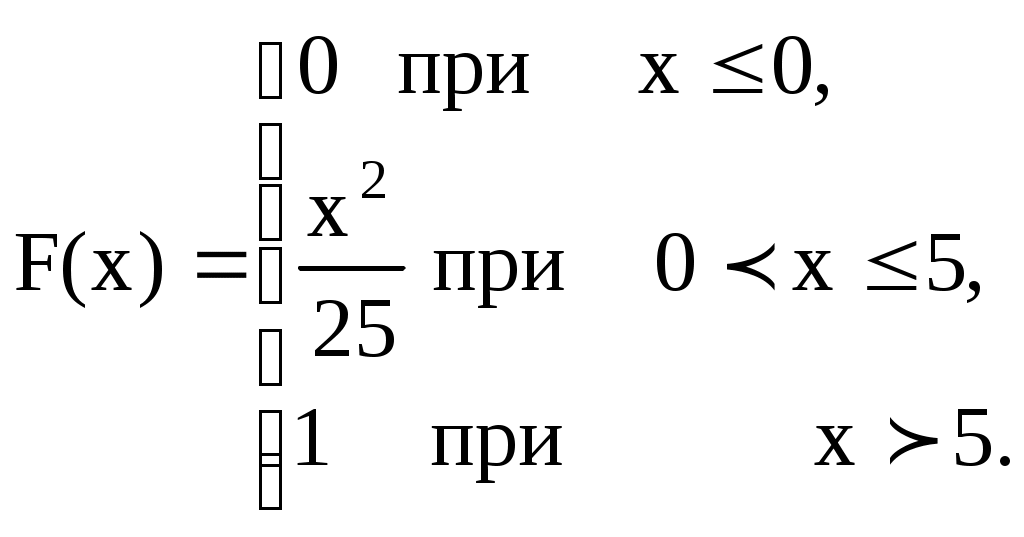

Найти математическое ожидание случайной величины .

14. Дано статистическое распределение выборки:



Найти выборочную среднюю.

15. Найти дисперсию случайной величины , если и несовместные