МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Название университета
Название факультета
Название кафедры
РЕФЕРАТ
На тему «Графы. Применение теории графов»
Работу выполнил:
Уткин Алексей Дмитриевич
Москва ‒ 2022
Содержание
1.Первые использования и открытия графов………………………………………………….3.
1.1 Первое использование диаграммы графов в науке………………………………..3.
1.2 Первое использование и открытие теории графов………………………………..3.
1.3 Второе открытие графов……………………………………………………………3. 1.4 Третье открытие графов…………………………………………………………….4. 1.5 Четвёртое открытие графов………………………………………...........................4. 1.6 Пятое открытие графов……………………………………………………………..5. 2.История возникновения теории графов……………………………………………………...5. 2.1 Теорема о четырёх красках………………………………………............................6. 2.2 Теорема Понтрягина-Куратовского………………………………………………..7.
3. Основные виды графов………………………………………………………………………6.
3.1 Ориентированные и неориентированные графы………………………………….6.
3.2 Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы……………………………………………………………………6.
3.3 Двудольный граф……………………………………………………………………7.
3.4 Эйлеров граф………………………………………………………………………...8.
3.5 Гальмитонов граф…………………………………………………………………...8.
3.6 Взвешенный граф……………………………………………………………………9.
3.7 Графы-деревья……………………………………………………………………….9.
4. Примеры применения теории графов……………………………………………………….9.
4.1 Комбинаторная оптимизация……………………………………………………….9.
4.2 Модели на простых графах………………………………………………………..10.
4.3 Модели на корневых деревьях…………………………………………………….10.
1.Первые использования и открытия графов
1.1 Первое использование диаграммы графов в науке
Диаграмма одной из разновидностей графа — дерева — использовалась издавна (конечно, без понимания, что это «граф»). Генеалогическое древо применялось для наглядного представления родственных связей. Но только античный комментатор работ Аристотеля финикийский философ и математик Порфирий использовал изображение дерева в науке как иллюстрацию дихотомического деления в своей работе «Введение» для классификации философского понятия материи.

Рис.1. Дерево Порфирия
1.2 Первое использование и открытие теории графов
Швейцарский, прусский и российский математик Леонард Эйлер в статье (на латинском языке, изданной Петербургской академией наук) о решении знаменитой задачи о кёнигсбергских, датированной 1736 годом, первым применил идеи теории графов при доказательстве некоторых утверждений. При этом Эйлер не использовал ни сам термин «граф», ни какие-либо термины теории графов, ни изображения графов. Леонард Эйлер считается отцом теории графов, открывшим понятие графа, а 1736 год назначен годом рождения теории графов.
1.3 Второе открытие графов
В 1847 году немецкий физик Густав Кирхгоф фактически разработал теорию деревьев при решении системы уравнений для нахождения величины силы тока в каждом контуре электрической цепи. Кирхгоф фактически изучал вместо электрической цепи соответствующий ей граф и показал, что для решения системы уравнений нет необходимости анализировать каждый цикл графа, достаточно рассмотреть только независимые циклы, определяемые любым остовым деревом графа.

 
Рис.2. Рис.3. Рис.4.
Рисунок 2 – электрическая цепь N.
Рисунок 3 – граф G, соответствующий электрической цепи.
Рисунок 4 – остовое дерево Т графа G.
1.4 Третье открытие графов В 1857 году английский математик Артур Кэли, занимаясь практическими задачами органической химии, открыл важный класс графов — деревья. Кэли пытался перечислить химические изомеры предельных (насыщенных) углеводородов CnH2n+2 с фиксированным числом n атомов углерода. 
Рис.5. Пример графа(дерево)
1.5 Четвёртое открытие графов
В 1859 году ирландский математик сэр Уильям Гамильтон придумал игру «Вокруг света». В этой игре использовался додекаэдр, каждая из 20 вершин которого соответствовала известному городу. От играющего требовалось обойти «вокруг света», то есть пройти по рёбрам додекаэдра так, чтобы пройти через каждую вершину ровно один раз.

Рис.6. Обход вершин додекаэдра на многограннике
1.6 Пятое открытие графов
В 1869 году французский математик Камиль Жордан придумал и исследовал деревья в рамках чистой математики. При этом Жордан использовал термины теории графов «вершина» и «ребро», но вместо термина «граф» было «соединение рёбер или просто «соединение».
2. История возникновения теории графов
2.1 Теорема о четырёх красках
Теорема о четырёх красках — теорема, утверждающая, что всякую расположенную на плоскости или на сфере карту можно раскрасить не более чем четырьмя разными цветами (красками) так, чтобы любые две области с общим участком границы имели разный цвет. При этом области должны быть связными, а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке не считаются для этих областей общей границей.
Теорема о четырёх красках относится к теории графов, так как каждая карта порождает граф следующим образом:
страны (включая внешнюю область) — это вершины;
вершины смежных стран соединяются ребром.

Рис.7. Проблема четырёх красок
Этот граф рисуется на плоскости без пересечения рёбер. Теорема о четырёх красках доказана, если доказано, что вершины любого подобного графа можно раскрасить четырьмя красками так, чтобы смежные вершины имели разные цвета.
Теорема о четырёх красках была доказана в 1976 году Кеннетом Аппелем и Вольфгангом Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация существования определённого набора из 1936 карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Авторы использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из 1936 карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен был бы содержать какую-нибудь из этих 1936 карт, чего нет. Это противоречие говорит о том, что контрпримера нет вообще.
Изначально доказательство было принято не всеми математиками, поскольку его невозможно проверить вручную. Чтобы развеять оставшиеся сомнения, в 1997 году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера.
2.2 Теорема Понтрягина — Куратовского Теория графов содержит топологические аспекты. Первым результатом в этом направлении является формула Эйлера в теории графов, полученная им в 1736 году. Следующий результат в виде теоремы Понтрягина — Куратовского был получен только через 191 год: в 1927 году советский математик Лев Семёнович Понтрягин доказал (но не опубликовал) этот результат, а в 1930 году польский математик Казимеж Куратовский опубликовал его. Планарный граф — это граф, который можно нарисовать на плоскости без пересечения рёбер. Граф, который нельзя так нарисовать, называется непланарным. Ниже показаны два важных непланарных графа, обозначаемых K5 и K3,3, их нельзя нарисовать на плоскости без пересечения рёбер.  
Рис.8. Полный граф K5 с пятью вершинами Рис.9. Полный двудольный граф K3,3
Теорема Понтрягина — Куратовского. Граф планарен тогда и только тогда, когда он ни в каком виде не содержит графов K5 и K3,3.
3. Основные виды графов
3.1 Ориентированные и неориентированные графы
Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.
Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами.
Неориентированный граф может быть представлен в виде ориентированного графа, если каждое его звено заменить на две дуги, имеющие противоположные направления.
3.2 Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Смешанным называют граф, в котором имеются рёбра хотя бы двух из упомянутых трёх разновидностей (звенья, дуги, петли).
Граф, состоящий только из голых вершин, называется пустым.
Мультиграфом называется граф, в котором пары вершин могут быть соединены более чем одним ребром, то есть содержащий кратные рёбра, но не содержащий петель.
Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным. Обыкновенный граф изображён на рисунке ниже.
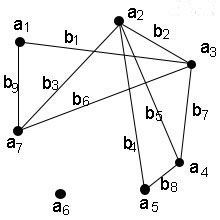
Рис.10. Обыкновенный граф
Граф заданного типа называют полным, если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном (рисунок ниже).
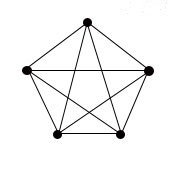
Рис.11. Обыкновенный граф
3.3 Двудольный граф
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Рис.12. Пример двудольного графа
3.4 Эйлеров граф
Эйлеровым графом называется граф, в котором можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример:
Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом? Объяснить ответ. Привести примеры.
Ответ: Если n - нечётное число, то каждая вершина инцидентна n-1 рёбрам. В таком случае данный граф является эйлеровым графом. Примеры таких графов на рисунке ниже.
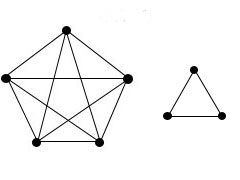
Рис.13. Примеры эйлерова графа
3.5 Гальмитонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, проходящий через все вершины рассматриваемого графа. Таким образом, говоря проще, гамильтонов граф - это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз. Пример гамильтонова графа - на рисунке ниже.
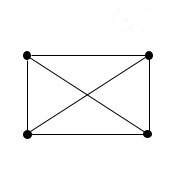
Рис.14. Гамильтонов граф
3.6 Взвешенный граф
Взвешенным графом называется граф, вершинам и (или) рёбрам которого присвоены "весы" - обычно некоторые числа. Пример взвешенного графа - транспортная сеть, в которой рёбрам присвоены весы, означающие стоимость перевозки груза по ребру и пропускные способности дуг. Пример взвешенного графа на рисунке ниже.
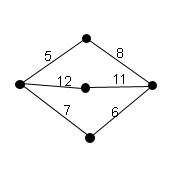
Рис.15. Взвешенный граф
3.7 Графы-деревья
Деревом называется связный граф без циклов (рисунок ниже). Любые две вершины дерева соединены лишь одним маршрутом.
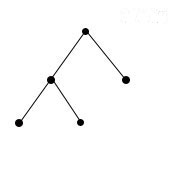
Рис.16. Граф-дерево
4. Примеры применения теории графов
4.1 Комбинаторная оптимизация
Вес ребра — один из наиболее часто используемых атрибутов графов, особенно при комбинаторной оптимизации. Например, вес ребра может представлять:
-транспортные расходы;
-время в пути;
-пространственное расстояние;
-потери мощности;
Существует проблемы, решаемые заданием атрибутов вершин в графовой модели. Например, вес вершины может представлять:
-стоимость производства;
-состояние узла в сети соединений;
-интервал времени в теории расписаний
4.2 Модели на простых графах
Социология. В социальной сети знакомств вершины — люди, а рёбра указывают на то, что соответствующие пары людей знают друг друга. Включение концепции самопознания требует в модели циклы самопознания, которым в графе соответствуют петли.
География. В географической модели вершины графа могут представлять страны (области, штаты), а рёбра — общую границу.
Проектирование вычислительных машин. Число процессоров соединяются вместе на одном чипе для многопроцессорного компьютера, который может выполнять параллельные алгоритмы. В графовой модели для такой сети взаимосвязей вершина — отдельный процессор, ребро — прямая связь между двумя процессорами. Спецификация параллельных архитектур иллюстрирует некоторые взаимодействия между теорией графов и абстрактной алгеброй.
Строительство. Двумерный каркас из стальных балок, соединенных шарнирами, которые позволяют каждой балке поворачиваться в плоскости, жёсткий, если ни одна из его балок не может поворачиваться. Проблема определения того, является ли каркас жёстким, может быть сведена к связности в двудольном графе.
Транспорт. Пусть стихийное бедствие обрушилось на регион, состоящий из небольших деревень. Вершины графа — деревни в регионе. Ребро указывает на то, что станция скорой медицинской помощи, созданная в одной из деревень, может также обслуживать другую. Тогда минимальное доминирующее множество графа описывает способ обслуживания региона с минимальным количеством станций первой помощи.
4.3 Модели на корневых деревьях
Базы данных. Многие информационные структуры информатики основаны на деревьях. Каталоги и подкаталоги (или папки и подпапки), содержащие файлы пользователя компьютера, обычно представляются операционной системой в виде вершин корневого дерева.
Теория алгоритмов. Конструирование больших компьютерных программ, реализующих сложные стратегии принятия решений, часто основано на корневых деревьях.
Информатика. Результирующее выражение будет отображаться в префиксной, постфиксной или инфиксной нотации в зависимости от того, какой из обходов используется. Для выражения инфикса требуются круглые скобки, которые можно включить в рекурсивный обход по порядку, создав левую круглую скобку в начале каждого обхода поддерева и правую — в конце каждого обхода поддерева.
Источники:
https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2
https://function-x.ru/
|
 Скачать 211.49 Kb.
Скачать 211.49 Kb.















