вариант 1. вариант 1 23.01. Исследование на экстремум. y Поскольку f(x)f(x), то функция является нечетной. Находим интервалы возрастания и убывания. Первая производная или
 Скачать 469.87 Kb. Скачать 469.87 Kb.
|
|
Задание № 1 Найти пределы функций , не пользуясь правилом Лопиталя А) 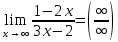 = = 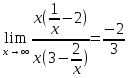 Б) 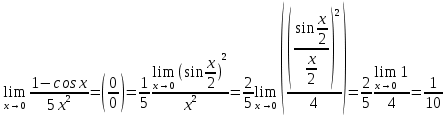 В) 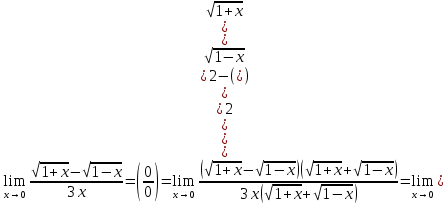 Г) 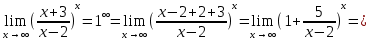 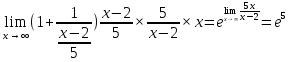 ЗАДАНИЕ № 11 Найдите производные данных функций А) y = 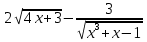 y’ = 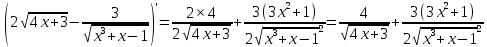 Б) y= 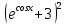 y’= 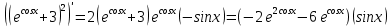 В) y= 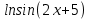 y’= 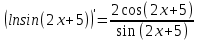 Г) 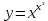 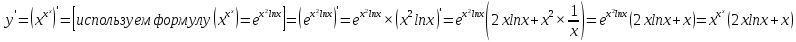 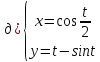 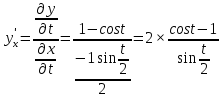 ЗАДАНИЕ № 21 Исследовать методом дифференциального исчисления функцию и используя результаты построить функцию 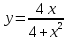 1) Область определения функции. X-любое Точки разрыва функции.- нет 2) Четность или нечетность функции. y(-x) = -y(x), нечетная функция 3) Периодичность функции. Непериодичная 4) Точки пересечения кривой с осями координат. Пересечение с осью 0Y x=0, y=0 Пересечение с осью 0X y=0 x1=0 5) Исследование на экстремум. y = 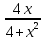 Поскольку f(-x)=-f(x), то функция является нечетной. 1. Находим интервалы возрастания и убывания. Первая производная. или Находим нули функции. Для этого приравниваем производную к нулю 16-4·x2 = 0 Откуда: x1 = 2 x2 = -2
В окрестности точки x = -2 производная функции меняет знак с (-) на (+). Следовательно, точка x = -2 - точка минимума. В окрестности точки x = 2 производная функции меняет знак с (+) на (-). Следовательно, точка x = 2 - точка максимума. 2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. или Находим корни уравнения. Для этого полученную функцию приравняем к нулю. Откуда точки перегиба: x1 = 0
6) Асимптоты кривой. Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: Находим коэффициент k: Находим коэффициент b: Получаем уравнение горизонтальной асимптоты: y=0 Найдем наклонную асимптоту при x → -∞: Находим коэффициент k: Находим коэффициент b: Получаем уравнение горизонтальной асимптоты: y=0 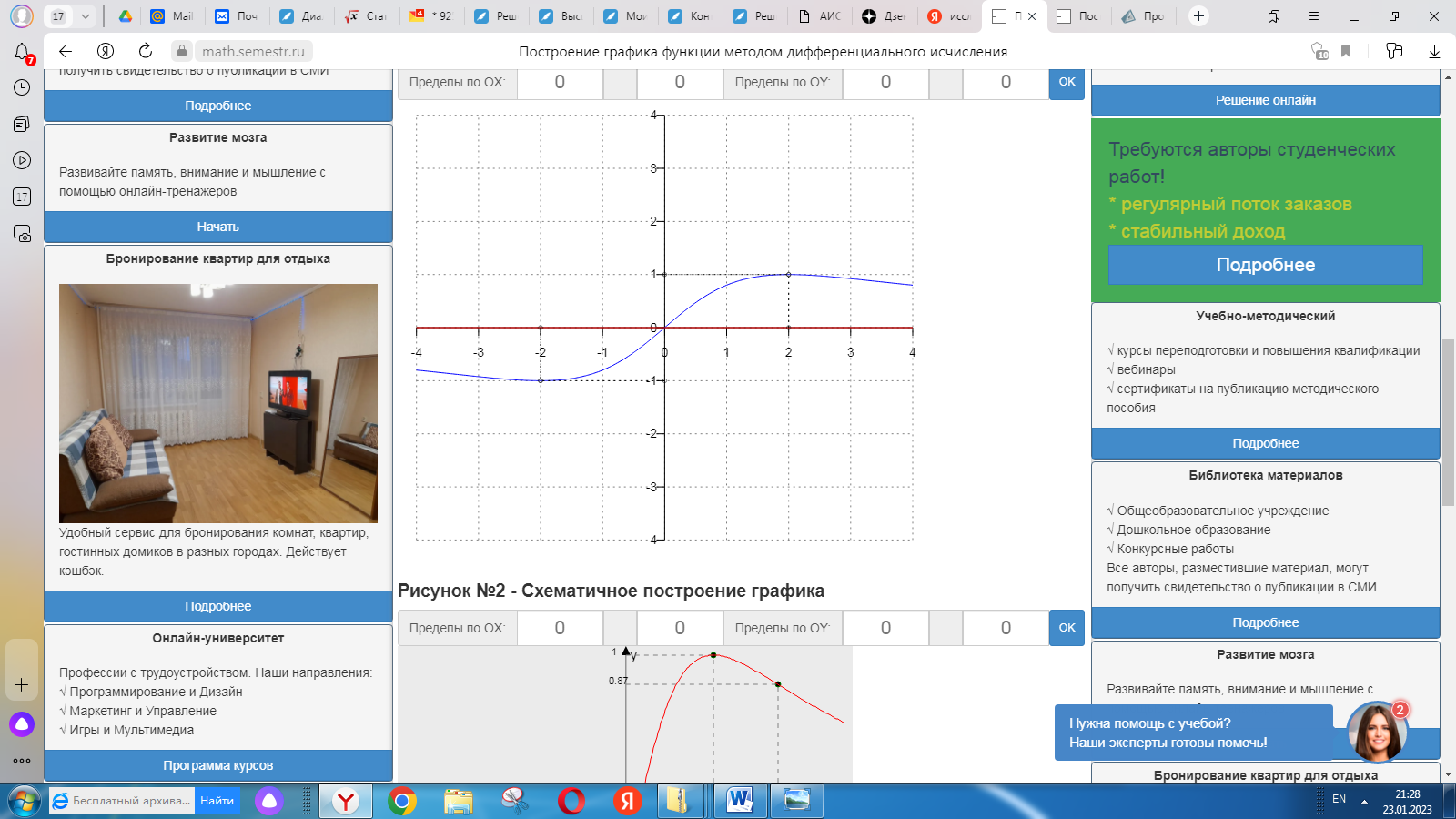 ЗАДАНИЕ № 31 Дана функция z=f(x, y). Найти : 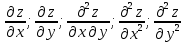 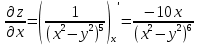 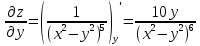 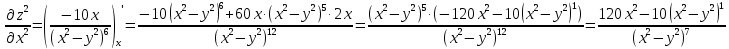 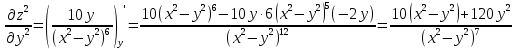 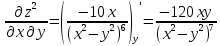 ЗАДАНИЕ № 41 Найти неопределенные интегралы. Результат проверить дифференцированием ( п. а и п.б) А) 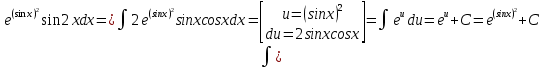 Проверка: 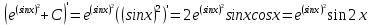 Б) 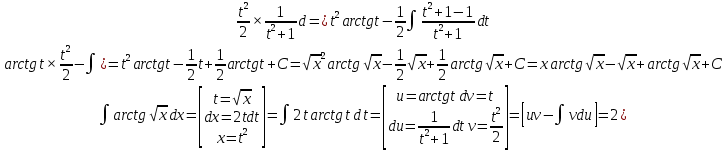 Проверка : 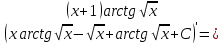 - -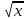 )’= )’== 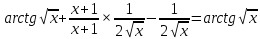 В)  * *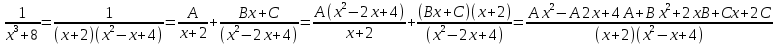 Соотнесем коэффициенты при одинаковых степенях: 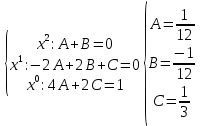 * 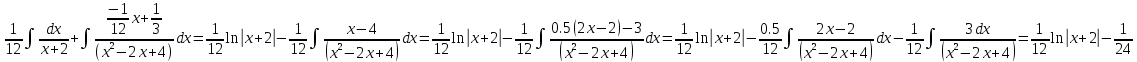 ln( ln(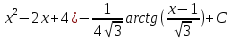 Г) 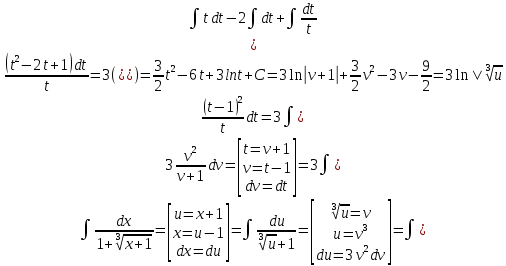 +1| + +1| +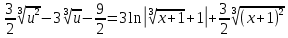 -3 -3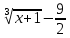 +C +C |
