реферат. ГБПОУ РМ1. История развития интегрального исчисления
 Скачать 261.26 Kb. Скачать 261.26 Kb.
|
|
ГБПОУ РМ «Саранский электромеханический колледж» Научно-исследовательская работа По математике на тему : «История развития интегрального исчисления» Выполнил: А.В. Студент группы 1-1 ИСиП Проверила: Т.П.Арюкова Оценка:________________ Дата сдачи:_____________ САРАНСК , 2021 Оглавление Оглавление…………………………………………………………………….2 Введение…………………………………………………………………….....3 I. История развития интегрального исчисления Геометрический смысл неопределенного интеграла……………….6 Неопределенный интеграл……………………………………………7 Символьный метод, операторы………………………………………8 Эйлер. Понятие об интегральной сумме…………………………….9 II .Проблема двойных и тройных интегралов Исследование методов двойных и тройных интегралов……………12 Основополагающий результат Коши………………………………...14 Заключение……………………………………………………………………16 Список литераторы……………………………………………………………17 Введение Цель данной работы: познакомиться с историей возникновения интегрального исчисления и показать его развитие . ИНТЕГРАЛ (or лат. Integer целый) - одно из важнейших понятий математики^ возникшее в связи с потребностью, с одной стороны отыскивать функции п£* их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой измерять площади, объемы, длины дуг, работу сил та определенный промежуток времени и т. п.  Символ интеграл введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования "восстанавливает" функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное: слово integer означает целый.  В ходе переписки И.Бернулли и Г.Лейбниц согласились с предложением Я.Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли. Другие термины, относящиеся к интегральному исчислению, появились значительно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее "примитивная функция", которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как "начальный": F(x)= - начальная (или первоначальная, или первообразная) для функции f(x), которая получается из F(x) дифференцированием. Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывающий метод, созданный Евдоксом Книдским (ок. 408 - ок. 355 до н. э.) и широко применявшийся Архимедом (ок. 287 - 212 до н. э.). Однако Архимед не выделил общего содержания интеграционных приемов и понятий об интеграле, а тем более не создал алгоритма интегрального исчисления. Ученые Среднего и Ближнего Востока в IX - XV веках изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в интегральном исчислении они не получили. Деятельность европейских ученых в это время была еще более скромной. Лишь в XVI и XVII веках развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождение квадратур (задачи на вычисление площадей фигур), кубатур (задачи на вычисление объемов тел) и определение центров тяжести . Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции. Например, криволинейную трапецию они представляли себе составленной из вертикальных отрезков длиной f(x) , которым тем не менее приписывали площадь, равную бесконечно малой величине f(x)dx. В соответствии с таким пониманием искомая площадь считалась равной сумме S = бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые сложенные в бесконечном числе, дают вполне определенную положительную сумму. В XVII веке были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П. Ферма уже в 1629 году решил задачу квадратуры любой кривой y =, где N - целое (т. е. вывел формулу ), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет, фактически опирался на идею приближенного интегрирования. И. Барроу (1603-1677 года), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функции в виде степенных рядов. I. История развития интегрального исчисления. 1. Геометрический смысл неопределённого интеграла. Пусть задан неопределенный интеграл F(x) + С для функции f(x) в некотором интервале. При фиксированном значении С – C1 получим конкретную функцию у1 = F(х) + С1:, для которой можно построить график. его называют интегральной кривой. Изменив значение С и положив С =С2 получим другую первообразную функцию С соответствующей новой интегральной кривой. Аналогично можно построить график любой первообразной функшш. Следовательно, выражение у=F(х) - С можно рассматривать как уравнение семейства интегральных кривых неопределённого интеграла F(х)+С. Величина С является параметром этого семейства каждом- конкретном значению С соответствует единственная интегральная кривая в семействе. Интегральную кривую, соответствующую значению параметра С2 можно получить из интегральной кривой, соответствующей значению параметра C1, параллельным сдвигом в направлении оси Оу на величину /С2 – С1/. 2.Неопределенный интеграл. Функция F(x) называется первообразной функцией для функции f(x) на множестве ХН R, если в каждой точке этого множества F'(x)= f(x). Например, функция F(x)= х2/2 является первообразной для функции f(х) = х так как (х2/2)' = х. Очевидно, что если F(x) - первообразная функция для функции f(x) на множестве X ,то функция F(х)+С, где С – некоторая постоянная, также является первообразной для функции f(x) , Xo X , так как (F(x)+С)' =F'(x)=f(x) Геометрически это означает, что если найдена одна кривая y= F(x),являющаяся первообразной, то, сдвигая ее вдоль оси ординат, мы снова получим кривые, удовлетворяющие условия (F(x)+С)'=f(x) . Метод подстановки Замена переменной интегрирования является одним из самых эффективных приемов сведения неопределенного интеграла к табличному. Такой прием называется методом подстановки или методом замены переменной. Он основан на следующей теореме. Пусть функция х = ф(t) определена и дифференцируема на некотором промежутке T, а X — множество значений этой функции, на котором определена функция f(x). Тогда, если функция f(x) имеет первообразную на X, то на Т справедлива формула 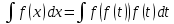 Доказательство. Пусть F(x) — первообразная для f(x) на X, то есть F'(x)=f(x). Используя правило дифференцирования сложной функции,получим 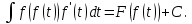 Так как Так как 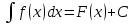 3.Символьный метод, операторы В наше время такие символы операций называют операторами. Операторы дифференцирования d() и интегрирования действуют на функции, “перерабатывая” их в другие, точно вычисляемые функции. Лейбниц разрабатывает особую алгебру действий с этими операторами. Он доказывает, что обычное число, а можно выносить за знак оператора. Одинаковые операторы можно выносить за скобку. Сокращенно все перечисленные свойства можно выразить соотношением: где a и b - числа. Однако в подходе Ньютона-Лейбница крылось серьёзное противоречие. Операторы, которые обладают таким свойством. называются линейными. Теория линейных операторов, которую с таким успехом начал развивать, Лейбниц,. в современной математике является хорошо разработанной и полезной в приложениях теорией. Многократное применение операторов можно принимать как степень оператора, например, для d( ) : То, что основные операторы математического анализа являются взаимно обратными Лейбниц подчёркивал своей символикой, утверждая, что в d(x) и также взаимно обратны, как степени и корни в обычном исчислении. Употребляя так же обозначение, аналогичное обозначению a -1 числа, обратного a , причём произведение a Ч a -1 =1. Обозначая операторы или наоборот: и понимая под их произведением последовательное их применение, имеем, т. е. произведение есть “единица”, не меняющая функцию. 4.Эйлер. Понятие об интегральной сумме Определение простого определенного интеграла по Лейбницу опиралось на понятие о бесконечно малых величинах, от которого математики XVIII века стремились освободить математический анализ. Это обстоятельство также способствовало укреплению точки зрения Ньютона. Это хорошо подтверждается тем, как Леонард Эйлер использовал понятие об интегральной сумме. Он не возражал против приближенного вычисления определенных интегралов при помощи соответствующих интегральных сумм, но рассматривать определенный интеграл как предел интегральной суммы не представлялось возможным, потому что этом случае все слагаемые интегральной суммы становились бесконечно малыми, то есть, с точки зрения Эйлера, были нулями. Быстро пробежимся по основным вехам эйлеровской биографии. В 1963 г. 23-летний Пауль Эйлер окончил курс теологии в Базельском университете. Но потому что учёных теологов было в те годы больше, чем требовалось, он получил официальную должность священника сиротского дома в Базеле лишь в 1701 г.. 19 апреля 1706 г. пастор Пауль Эйлер женился на дочери священника. А 15 апреля 1707 г. у них родился сын, названный Леонардом. Начальное образование будущему учёному дал отец, учившийся некогда математике у Якоба Бернулли. Отец готовил старшего сына к духовной карьере, но, несмотря на это, однако занимался с ним и математикой – как в качестве развлечения, так и для развития логического мышления. Мальчик увлёкся математикой, стал задавать отцу вопросы один сложнее другого. Когда у Леонардо проявился интерес к учёбе, его направили в Базельскую латинскую гимназию – под надзор бабушки. 20 октября 1720 г. 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета. Мечта отца о том, что бы Эйлер стал священником сбывалась. Но любовь к математике, блестящая память и отличная работоспособность сына направили молодого учёного по иному пути. Он легко усваивал учебные предметы, отдавая предпочтение математике. И естественно, что способный мальчик вскоре обратил на себя внимание Бернулли, который посоветовал юноше читать математические мемуары, а по субботам пригласил приходить к нему домой, чтобы совместно разбирать прочитанное. В доме своего учителя Эйлер подружился с сыновьями Бернулли – Николаем и Даниилом, также увлечённо занимавшимися математикой. А 8 июня 1724г. 17-летний Леонард Эйлер произнёс по- латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона - и был удостоен учёной степени магистра (в XIX в. в большинстве университетов Западной Европы ученая степень магистра была заменена степенью доктора философии). Эйлер просто не мог не заниматься математикой или её приложениями. В 1735 г. Академия получила задание выполнить срочное и очень громоздкое астрономическое вычисление. Эйлер взялся выполнить работу за 3 дня – и справился самостоятельно, в то время, как группа признанных академиков просила на эту работу три месяца. Перенапряжение не прошло бесследно: Эйлер заболел и потерял зрение на правый глаз. Но талантливый учёный отнёсся к несчастью с величайшим спокойствием: “Теперь я меньше буду отвлекаться от занятий математикой”, - философски заметил он. До этого Эйлера знал лишь узкий круг учёных. Мировую славу ему принесло двухтомное сочинение “ Механика, или наука о движении, в аналитическом изложении ”, изданное в 1736 г, где Эйлер блестяще применил методы математического анализа к решению проблем движения в пустоте и в сопротивляющейся среде. “Тот, кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью и без всякой помощи прочитает работу полностью”, - заканчивает Эйлер своё предисловие к книге. Леонард Эйлер начал прокладывать аналитический путь развития точных наук, применения дифференциального и интегрального исчисления для описания физических явлений, который требовал дух времени. Концепция Ньютона и до последней четверти XVIII века сталкивалась с трудностями. В этот период встречались элементарные функции, первообразные которых не могут быть выражены через элементарные функции, математики знали и некоторые несобственные интегралы, в том числе и расходящиеся. Но такого рода факты были единичными и установившейся эффективной концепции интеграла нарушить не могли. Положение изменилось лишь в последней четверти XVIII и, особенно, в начале XIX века. С 70-х годов XVIII века решение задач аналитической механики, физики и других дисциплин потребовало продолжения развития понятия и употребления определенного интеграла, особое значение приобретают двойные и тройные интегралы (Эйлер, Лагранж, Лаплас и др.). К этому времени великие идеи Ньютона и Лейбница были только-только опубликованы, и современный математический анализ только начал создавался. Эти идеи породили мощные методы, которые стали применять во всех отраслях точного знания. Применение это шло рука об руку с развитием самого анализа, часто указывая пути, по которым должно развиваться новое исчисление. II. Проблема двойных и тройных интегралов 1.Исследование методов двойных и тройных интегралов Эта эпоха математического творчества оказалась единственной по своей интенсивности, а Эйлер - одним из немногих по своей продуктивности учёным. Его творения: "Введение в анализ бесконечно малых", "Основания дифференциального исчисления" и "Основания интегрального исчисления" стали первыми трактатами, которые объединили уже обширный, но вместе с тем разрозненный материал нового анализа в цельную науку. В них была разработана та основа современного анализа, которая сохранилась и до нашего времени. Исследование методов вычисления двойных и тройных интегралов показала, что вычисление этих интегралов методом вычисления обычного определенного интеграла - при помощи неопределенного, невероятно трудно, поэтому математики сохранили концепцию Ньютона только на словах, а на деле, при решении задач точных наук, приняли сторону Лейбница. Так они вычисляли соответствующие интегральные суммы (в прямоугольных, цилиндрических и сферических координатах) и находили их пределы. Таким образом, поиск методов вычисления новых видов определенного интеграла показал, что обыкновенный, двойной и т. д. определенный интегралы должны быть обоснованы сами по себе независимо от понятия неопределенного интеграла. Но каждое слагаемое любой интегральной суммы является бесконечно малой величиной. Ставился вопрос не только о легализации ранее “изгоняемого” понятия бесконечно малого, но и о раскрытии его реального содержания и о соответствующем его применении. Как говорилось ранее, чтобы всё это сделать, появилась необходимость преодолеть, обобщить, развить традиционное, каким было признано Эйлерово, толкование функции и понятия предела. Коши - решение парадокса существования конечных сумм из бесконечно малых слагаемых. Возник естественный вопрос о возможности существования пределов интегральных сумм, имеющих бесконечно малые слагаемые. Так в первой четверти XIX века, избегаемое ранее, понятие бесконечно малой оказалось необходимым и для изучения и для сопоставления свойств непрерывных и разрывных функций. 2.Основополагающий результат Коши Основополагающих результатов добился в развитии этого вопроса Коши. “Между многими понятиями, - указывал Коши, - тесно связанными со свойствами бесконечно малых, следует поместить понятие о непрерывности и прерывности функций”. Здесь же Коши дал определение непрерывности функции, которое более чем ясно подтвердило ясность этого его утверждения. Новая постановка задач обоснования математического анализа дала понять, что вопрос не только в признании и применении бесконечно малых - это делали и раньше! - но прежде всего в научном истолковании их содержания и обоснованном на этом использовании их в алгоритмах математического анализа. Но, чтобы этого добиться, необходимо было преодолеть господствовавшее в XVIII веке узкое толкование понятия предела, разработать новую общую теорию пределов. Исследование разрывных функций, а также сравнение их с функциями непрерывными заставило признать то, что ранее считалось невозможным: предел, к которому стремиться последовательность значений функции, при стремлении аргумента в некоторой точке может оказаться отличным от значения функции в этой точке. Получается, что предел не всегда является конечным значением переменной, но во всех случаях предел является числом, к которому переменная неограниченно стремится. Следовательно, dx и dy не необходимо нули или “мистически” актуально бесконечно малые; бесконечно малая - это переменная, имеющая пределом нуль, причем факт не является противоречием или парадоксом. Вторую ограничительную тенденцию в принятой ранее трактовке понятия предела также преодолел Коши. Он признал, что переменная может приближаться к своему пределу не только монотонно, но и колеблясь - принимая порой значения, равные её пределу. Эта формулировка придала теории Коши необходимую общность и исключительную гибкость. Заключение Интеграл используется в таких науках как физика, геометрия, математика и других науках. При помощи интеграла вычисляют работу силы, находят координаты центр масс, путь пройденный материальной точкой. В геометрии используется для вычисления объема тела, нахождение длины дуги кривой и др. Математики до сих пор следуют пути, намеченному Огюстеном Луи Коши, но лишь с теми усовершенствованиями, которые внёс во второй половине XIX века К. Вейерштрасс. Работы Коши и Вейерштрасса завершили создание классического математического анализа, подведя итог многовековому развитию интегрального исчисления. Трудно представить, как жили бы люди, если бы не умели считать, измерять, сравнивать. Этому учит математика. С числами и цифрами приходится иметь дело всем. Вряд ли кто-то станет отрицать необходимость математических знаний. Ведь математика учит человека думать, анализировать, развивает логическое мышление, память. Математические знания нужны человеку любой профессии. Без математики строитель не сможет построить дом, летчик - поднять в воздух самолет, машинист не поведет поезд. Кроме этого, благодаря математике появилось много других новых наук и профессий, появились вычислительные машины, компьютеры. Очень важно знать математику в наше время. Ведь математика основа точных наук. Без них невозможно построить корабль и самолет, автомобили и метрополитены, даже строительство домов требует точности. Любовь к точным наукам развивает умение логически мыслить, анализировать, смотреть на вещи другими глазами и давать точное определение. Список литературы 1.Богомолов Н.В. Математика: учеб. для ССУЗов/Н.В. Богомолов, П.И. Самойленко .-3-е изд., стереотип.-М.: Дрофа, 2008.-395с. 2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для ССУЗов/ Н.В.Богомолов.-5-ое изд., стер.-М.: Высшая школа., 2008.-495 с. 3.Пирумов У.Г. Численные методы: учебное пособие для студентов ССУЗов/ У.Г. Пирумов.-4-е изд., испр. –М. : Дрофа, 2008.-224с. 4.Высшая математика для экономистов:учебник для студентов ВУЗов/ под редакцией Н.Ш. Кремера.-3-е изд.-М.: ЮНИТИ-ДАНА, 2008.-479 с.-(Серия « Золотой фонд российских учебников») 5.Пехлецкий И.Д. Математика: учебник для средних специальных учебных заведений/И.Д. Пехлецкий. -5 изд., стер.-М.: Академия, 2009г.-421с 6.Опорный конспект по алгебре и началам анализа /под редакцией преподавателя ФГОУ СПО ЧЮТ Кондратьевой Е.А.-Ч.: ЧЮТ, 2009 г. –56с |
