Колебания. Колебания и волны

• Название: Колебания и волны
• Анкор: Колебания
• Дата: 23.08.2022
• Размер: 0.72 Mb.
• Имя файла: kol_vol.doc
• Тип: Закон; #651336
• страница: 1 из 3

КОЛЕБАНИЯ И ВОЛНЫ
Кинематика гармонических колебаний
Колебаниями называются процессы, повторяющиеся во времени. Механические периодические колебания описывают движение, повторяющиеся через одинаковые промежутки времени. Колебания, происходящие по закону синуса или косинуса, называются гармоническими и описываются уравнением гармонических колебаний:

,

где x – смещение колеблющейся точки (тела) относительно положения равновесия;

A - амплитуда колебания, равная максимальному смещению;

φ= – фаза колебания, определяет долю смещения от амплитуды;

–начальная фаза – фаза в начальный момент времени;

ω - циклическая частота, связанная с частотой колебания соотношением ω=2пν;

ν – частота, равна числу колебаний за одну секунду;

T – период колебания - время одного колебания, из определения следует соотношение .

График гармонического колебания представлен на рисунке 1.



Рис.1

Скорость колеблющейся точки, согласно определению скорости, находится следующим образом

υ= = )

видно, что, как и смещение, изменяется по гармоническому закону, а коэффициент перед гармонической функцией имеет смысл максимальной скорости:

= Aω.

Ускорение определяется повторным дифференцированием:

a= =- ( )

а максимальное ускорение равно:

=Aω².

Система, в которой происходят гармонические колебания, называется гармоническим осциллятором.

Гармонические колебания изображаются с помощью векторной диаграммы, в которой вектор, длиной А представляется вращающимся против часовой стрелки, при этом фаза колебания определяется углом между вектором и осью (Рис . 2).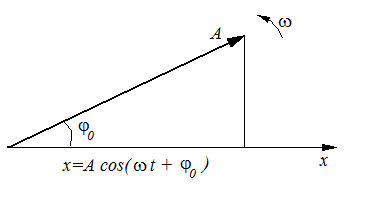



Рис.2

Дифференциальное уравнение гармонических колебаний
Подстановка выражения ( ) во второй закон Ньютона

=

позволяет определить характер сил, под действием которых возникают гармонические колебания:

,

Силы, подчиняющиеся этому закону, называются квазиупругими (как бы упругими) и имеют свойства:

1. 
   силы пропорциональны смещению;
   
2. 
   являются возвращающими, т.е. направлены в сторону, противоположную смещению,
   

k – коэффициент квазиупругой силы.

Таким образом, для возникновения гармонических колебаний необходимы квазиупругие силы.

Преобразование уравнения, записанного по второму закону Ньютона

ma = F,

дает

m = - kx

или

m + kx = 0,

.

Таким образом, если принять , то дифференциальное уравнение гармонических колебаний имеет вид:

+ ω²x = 0.

Решением этого уравнения является уравнение гармонического колебания

.

Примеры гармонических осцилляторов

1. 
   Пружинный маятник состоит из невесомой пружины, жесткостью k и подвешенного к ней груза массой m.
   

В данной системе колебания происходят под действием силы упругости , следовательно, циклическая частота и период колебаний пружинного маятника равны:

ω = , T= 2 /ω = 2

2. 
   Математический маятник – это маленький груз массой m, подвешенный на легкой нерастяжимой нити длиной l.
   

По второму закону Ньютона

,

где -сила тяжести, - сила натяжения нити (Рис. 3).




В проекции на направление, касательное к траектории, уравнение имеет вид:

m = -mg sin α

или

m = - mgsinα.

Поскольку

x = αl,α = x/l,

то

m + mgsinx/l=0.

П
Рис.3
олученное уравнение будет описывать гармонические колебания только при малых углах отклонения. Если

α < 15º , тоsinα ≈ α,

тогда

.

Такое уравнение совпадает с дифференциальным уравнением гармонических колебаний

+ ω² x=0,

и циклическая частота математического маятника равна

ω = .

Таким образом, только малые колебания математического маятника являются гармоническими.

3. 
   Физический маятник это любое массивное тело, которое может вращаться относительно оси, не проходящей через центр масс тела.
   

Сила тяжести создает вращательный момент (Рис. 4)




M=- mg· l· Sinα

Основное уравнение динамики вращательного движения



приводит к соотношениям:

,

или

,

где I – момент инерции тела относительно данной оси, - угловое ускорение тела.

Для малых углов (α < 15º , sin ≈ α)


Рис.4
,



получено дифференциальное уравнение гармонических колебаний физического маятника в стандартном виде

,

и его решение



циклическая частота физического маятника

ω= .
Энергия гармонических колебаний
Кинетическая энергия точки, колеблющейся с начальной фазой =0, равна
= ,

Видно, что кинетическая энергия колеблется с удвоенной частотой по сравнению с частотой самого колебания.

Потенциальная энергия равна отрицательной работе квазиупругой силы
= .

Потенциальная энергия также колеблется с частотой , но со сдвигом по фазе на относительно кинетической энергии.

Полная механическая энергия гармонического осциллятора не изменяется с течением времени, при колебаниях происходит взаимное превращение кинетической и потенциальной энергии. Это видно из следующих выкладок:

= +
Электромагнитные колебания в колебательном контуре
Простейший колебательный контур – это электрическая цепь, состоящая из конденсатора электроемкостью С и соединенной с ним последовательно катушки индуктивностью L (Рис. 5).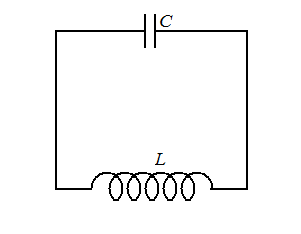




При замыкании на катушку предварительно заряженного конденсатора в колебательном контуре возникают свободные колебания заряда конденсатора и тока в катушке индуктивности.

Свободные колебания являются гармоническими, если в контуре полностью отсутствует сопротивление (R=0).

П
Рис. 5
ри зарядке конденсатора в его электрическом поле запасается энергия

,

где - максимальный заряд на конденсаторе.

При замыкании цепи энергия из электрического поля переходит в магнитное поле. В момент полного разряда конденсатора ток и энергия в магнитном поле достигают максимального значения

,

здесь - максимальный ток в цепи.

За счет явления самоиндукции, ток в цепи продолжает идти до полного исчезновения, при этом происходит обратный переход энергии из магнитного в электрическое поле и заряд на конденсаторе достигает первоначального значения. Дальше процесс повторяется в обратную сторону, поскольку сопротивление равно нулю, этот процесс будет происходить бесконечно долго.

Таким образом, и при электромагнитных колебаниях, также как и при механических, полная энергия, переходя из одного вид в другой, сохраняется
.

Дифференциальное уравнение гармонических колебаний величины заряда выводится из закона Ома, имеющего в данном случае вид
U_С = ,

где - напряжение на конденсаторе, - ЭДС самоиндукции. С учетом, что сила тока равна

,

можно записать



или

.

Таким образом, дифференциальное уравнение и его решение имеют вид

+ ω² q = 0, q= cos ( ωt+ ),

где ω = - циклическая частота, - период колебаний.

Напряжение на конденсаторе, как и заряд, изменяется по гармоническому закону

U_С= cos (ωt+ ),

сила тока колеблется с такой же частотой, но со сдвигом по фазе на относительно напряжения:



Переменный ток, возникающий в цепи, называется квазистационарным, если его мгновенное значение в данный момент времени во всех точках цепи одинаково. Это возможно благодаря большой скорости распространения электромагнитного поля, равной скорости света, для не слишком больших размеров контуров.

Сложение гармонических колебаний
Сложение колебаний означает поиск результирующего колебания, если система (точка) одновременно участвует в нескольких колебательных процессах.

Пусть некоторое колебание описывается законом . На векторной диаграмме вектор длиной А представляется вращающимся против часовой стрелки со скоростью (Рис.6). Положение вектора в начальный момент времени задается углом , тогда проекция конца вектора А совершает гармоническое колебание по закону .

Рис.6

1. 
   При сложении двух колебаний в одинаковых направлениях и одинаковыми частотами
   

,

,

результирующее колебание можно найти с помощью векторной диаграммы. Оба колебания на векторной диаграмме изображаются двумя векторами (рис.7), угол между которыми равен . Вектор, равный сумме этих векторов, представляет результирующее колебание с амплитудой



и начальной фазой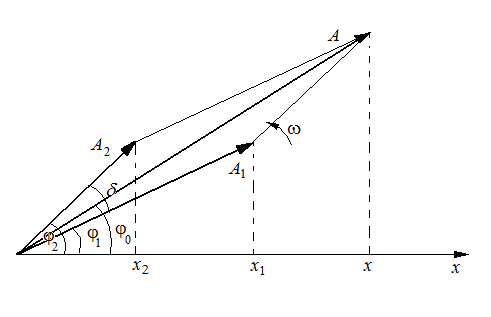

.




Рис. 7

2. 
   Сложение колебаний одного направления с близкими частотами (биения): пусть частота одного колебания ω, другого ω+∆ω, причем ∆ω<<ω.
   

Уравнения складываемых колебаний имеют вид:

.

Складывая алгебраически и применяя тригонометрическую формулу, получим

,

здесь учтено, что ∆ω<<ω, это позволяет во втором множителе пренебречь по сравнению с ω.

Полученный результат можно интерпретировать как уравнение колебания с частотойω, амплитуда которого изменяется по закону , это значит, что амплитуда пульсирует с частотой ∆ω. Такие колебания называются биениями, а ∆ω- частота биений.

3. 
   Сложение взаимно перпендикулярных колебаний.
   

Пусть начальная фаза одного колебания равна нулю, другого - . Тогда складываемые колебания описываются уравнениями:



где разность фаз обоих колебаний.

Рассмотрим частные случаи:

а) Пусть =0, тогда



поделив второе уравнение на первое, получим

,

это значит, что колебание происходит вдоль прямого отрезка, наклоненного к оси Х под углом

.
При уравнение траектории имеет вид

.

б) Пусть , тогда



или



Возведение уравнений в квадрат с последующим их сложением дает:
,

Это уравнение эллипса, оси которого совпадают с осями координат. При А=В эллипс вырождается в окружность.
в) В общем случае, когда складываются взаимно перпендикулярные колебания с одинаковыми частотами



уравнение траектории получается путем исключения параметра t.

Запишем уравнения в виде:



Учтем, что

,

получим уравнение эллипса
,

ориентация осей которого зависит от амплитуд складываемых колебаний и разности фаз .

г) Когда частоты складываемых колебаний разные, наиболее интересный случай при соотношении частот равном отношению целых чисел:



точка движется по замкнутой траектории, называемой фигурой Лиссажу. Вид фигуры Лиссажу зависит от соотношения частот , разности фаз и амплитуд складываемых колебаний.