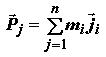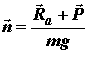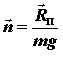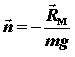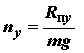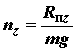госы Техническая эксплуатация и восстановление авиационных электросистем и пилотажно-навигационных комплексов боевых летательны. Колебания системы с одной степенью свободы
 Скачать 118.28 Kb. Скачать 118.28 Kb.
|
|
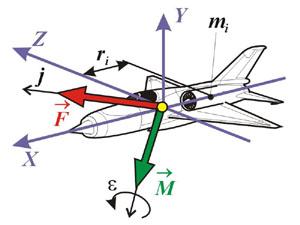
Задание 15 1. Малые колебания консервативной системы с одной степенью свободы около положения устойчивого равновесия. Свободные колебания. Случай произвольной возмущающей силы. Колебания системы с одной степенью свободы Рассмотрим консервативную систему с одной степенью свободы, движение которой описывается уравнением Лагранжа второго рода d dt ∂T ∂q˙ − ∂T ∂q = − ∂Π ∂q , где q — обобщенная координата, а T и Π кинетическая энергия и потенциальная энергии, причем T = 1 2 A(q) ˙q 2 , Π = Π(q). Пусть q = 0 соответствует положению равновесия. Тогда dΠ dq (0) = 0, Потенциальная энергия Π определяется с точностью до произвольной аддитивной постоянной, поэтому без ограничения общности можно считать, что Π(0) = 0. Разложим функции T и Π в ряды Тейлора в окрестности точки q = 0. Учитывая, что первые два члена в разложении функции Π равны нулю, получим T = T0 + . . . , Π = Π0 + . . . , где T0 = 1 2 a0q˙ 2 , Π0 = 1 2 c0q 2 , a0 = A(0), c0 = d 2Π dq2 (0) Предположим, что c0 > 0. Тогда потенциальная энергия Π имеет минимум в точке q = 0, и из теоремы Лагранжа следует, что положение равновесия устойчиво. Пусть в начальный момент времени значения q и q˙ малы. Тогда в силу устойчивости положения равновесия они будут малы в любой другой момент времени, поэтому T ' T0, Π ' Π0. Подставив приближенные значения T0 и Π0 кинетической и потенциальной энергии в уравнение Лагранжа, получим уравнение малых колебаний системы с одной степенью свободы: a0q¨+ c0q=0. Данное уравнение аналогично уравнению, mx¨ + cx = 0. описывающему колебания груза массой m прикрепленного к пружине жесткости c. В связи с этим постоянную a0 называют приведенной массой, а величину c0 — приведенной жесткостью. Решение уравнения малых колебаний системы с одной степенью свободы имеет вид x = A sin(ωt + α), где A и α — произвольные постоянные, ω = p c0/a0 частота колебаний. Если c0 < 0, то положение равновесия оказывается неустойчивым, и малые колебания вблизи такого положения равновесия невозможны. Пусть q = q0 — положение равновесия q 0 = q − q0. Тогда a0 = A|q 0=0 = A(q0), c0 = d 2Π dq02 ¯ ¯ ¯ ¯ q 0=0 = d 2Π dq2 (q0). Этими формулами удобно пользоваться при решении задач, в которых положению равновесия соответствует ненулевое значение обобщенной координаты. Свободные колебания при наличии сопротивления Пусть на систему с n степенями свободы, совершающую малые колебания относительно устойчивого положения равновесия q1 = q2 = · · · = qn = 0, действуют диссипативные силы Qj = − ∂R ∂q˙j , R = 1 2 Xn j=1 Xn k=1 Bjkq˙j q˙k, где функция Релея R является положительно определенной квадратичной формой, Bjk = Bkj . Разложим функцию R ряд Тейлора в окрестности положения равновесия: R = R0 + . . . , R0 = 1 2 Xn j=1 Xn k=1 bjkq˙j q˙k, bjk = Bjk(0, . . . , 0). Квадратичная форма b = Xn j=1 Xn k=1 bjkqj qk, также как и квадратичные формы a и c, является симметричной и положительно определенной. Уравнения малых колебаний при наличии сопротивления имеют вид d dt ∂T0 ∂q˙j + ∂R0 ∂q˙j + ∂Π0 ∂qj = 0, j = 1, 2, . . . , n или Xn k=1 (ajkq¨k + bjkq˙k + cjkqk) = 0, j = 1, 2, . . . , n Запишем эти уравнения в матричной форме: Aq¨ + Bq˙ + Cq = 0 и будем искать их решение в виде q = ue µt . Для определения u получаем систему линейных алгебраических уравнений (Aµ2 + Bµ + C)u = 0, (9.22) которая имеет нетривиальное решение, если det(Aµ2 + Bµ + C) = 0 (9.23) Уравнение (9.23) для определения µ степени 2n имеет 2n корней µ1, µ2, . . . , µ2n. Каждому корню µk соответствует нетривиальное решение uk системы уравнений (9.22). Если уравнение (9.23) не имеет кратных корней, то векторы uk линейно независимы и общее решение системы уравнений малых колебаний имеет вид q = X 2n k=1 Ckuke µkt . 23 Покажем, что для любого корня µ = γ + iδ уравнения (9.23) выполняется неравенство Re(µ) = γ < 0. Пусть u = v + iw — соответствующее µ нетривиальное решение системы уравнений (9.22). Тогда имеет место тождество (Aµ2 + Bµ + C)(v + iw) = 0. Умножив это тождество слева на u = v − iwT , получим pµ2 + qµ + r = 0, (9.24) где p = (v − iw) T A(v + iw), q = (v − iw) T B(v + iw), r = (v − iw) T C(v + iw), причем v 2 + w 2 6= 0. Преобразуем выражение для p: p = v T Av − iwT Av + iv T Aw + wT Aw. Благодаря симметрии квадратичной формы a имеет место равенство wT Av = v T Aw. Следовательно, в силу положительной определенности квадратичной формы a и условия v 2 + w 2 6= 0 p = v T Av + wT Aw = a(v) + a(w) > 0. Ввиду того, что квадратичные формы b и c тоже симметричные и положительно определенные, аналогичным образом получаем, что q = b(v) + b(w) > 0, r = c(v) + c(w) > 0. Число µ совпадает с одним из корней уравнения (9.24) µ1 = −q + p q 2 − 4pr 2p , µ2 = −q − p q 2 − 4pr 2p . Если q 2 − 4pr < 0, то оба корня имеют отрицательную вещественную часть, так как p > 0 и q > 0. Если q 2 − 4pr > 0, то p q 2 − 4pr < q благодаря тому, что p > 0, r > 0, и оба корня отрицательны, так как q > 0. Следовательно, Re(µk) < 0 при k = 1, 2, . . . 2n и общее решение q = X 2n k=1 Ckuke µkt → 0 при t → 0, т. е. свободные колебания затухают. При малом сопротивлении коэффициент q в уравнении (9.24) мал и корни µk являются комплексными. Комплексное общее решение q можно преобразовать к вещественному виду. Уравнение (9.23) имеет вещественные коэффициенты, поэтому его комплексные корни образуют комплексно сопряженные пары. Рассмотрим два линейно независимых решения, соответствующих комплексно сопряженным корням γ + iδ и γ − iδ: q + = (v + iw)e (γ+iδ)t , q − = (v − iw)e (γ−iδ)t Линейную комбинацию решений q + и q − в общем решении можно заменить линейной комбинацией двух вещественных решений q + + q − 2 = e γt(v cos δt − w sin δt), q + − q − 2i = e γt(v sin δt + w sin δt). Выполнив такую замену для всех комплексных корней, получим вещественное общее решение. 2. Особенности устройства барометрических высотомеров. Барометрический высотомер предназначен для определения барометрической высоты или относительной высоты полёта. Принцип действия барометрического высотомера основан на измерении давления атмосферы. Известно, что с увеличением высоты уменьшается и атмосферное давление. Данный принцип положен в основу прибора, который на самом деле измеряет не высоту, а давление воздуха. Конструктивно прибор состоит из запаянной коробочки с мембраной, изменение положения которой механически связано со стрелками, перемещающимися вокруг шкалы, проградуированной в цифрах. На машинах со сравнительно низким практическим потолком (на Ан-2 и большинстве других поршневых самолётов, на вертолётах) установлен двустрелочный высотомер ВД-10 или аналогичный зарубежный, подобный обычным часам — только циферблат разделён не на 12, а на 10 секторов, каждый сектор для большой стрелки означает 100 м, а для маленькой — 1000 м. Аналогичный по конструкции высотомер ВД-20 (высотомер двустрелочный на высоту до 20 км), установленный, например, на Ту-134, имеет отдельную градуировку циферблата для короткой стрелки до 20 км. Примечательно, что данная конструкция стала де-факто международным стандартом. Другие высотомеры, например, УВИД-15, имеют лишь длинную стрелку (один оборот за 1000 м или 1000 фт высоты), а полная высота отображается цифрами в окне. Точность измерения барометрических высотомеров (допустимая погрешность измерений) определяется действующими стандартами и лежит, как правило, в пределах до 10 м. Высота полёта воздушного судна над земной (либо водной) поверхностью вычисляется по разности давления воздуха в точке нахождения судна и давления на поверхности, над которой оно находится. Атмосферное давление на поверхности (как правило, в районе аэродромов посадки, горных массивов либо крупных опасных препятствий) сообщается экипажу наземными службами. Для правильного отображения высоты полёта на приборе необходимо вручную установить величину атмосферного давления на земле (или давление, приведённое к уровню моря). Неправильная установка экипажем такого давления при полётах с нулевой видимостью не раз становилась причиной авиакатастроф. Нужно отметить, что в авиации могут применяться несколько вариантов установки давления барометрического высотомера. В России и некоторых странах СНГ при полетах ниже эшелона перехода (ниже нижнего эшелона) принято устанавливать давление аэродрома (при заходе на посадку и вылете) или минимальное давление на маршруте, приведённое к уровню моря (при полетах по маршруту). В большинстве стран мира ниже нижнего эшелона отсчет высоты выполняют по давлению, приведенному к уровню моря. Для полётов по воздушным трассам (выше высоты перехода) в авиации используется понятие эшелон, то есть условная высота, измеренная до изобары (условной линии постоянного давления) 760 мм рт. ст., она же 1013 мбар (гПа) или 29,92 дюйма рт. ст. Установка на всех воздушных линиях всеми без исключения воздушными судами одинакового давления на барометрических высотомерах создаёт единую для всех систему отсчёта, позволяющую осуществлять безопасное воздушное движение. Снижение воздушного судна на посадку без достоверной информации об атмосферном давлении в районе аэродрома категорически запрещается. По требованиям ИКАО на всех воздушных судах устанавливается т. н. диспетчерский высотомер (например, типа УВИД), который, помимо показа высоты на шкале, выдаёт сигнал высоты самолётному ответчику, благодаря чему авиадиспетчер может видеть на экране точную высоту воздушного судна. Парашютный высотомер — это обычный барометрический высотомер с удобным креплением на руку. Предназначен для измерения и визуального контроля высоты в свободном падении и при спуске на раскрытом парашюте, а также для определения атмосферного давления. Имеет малый размер и массу (площадь циферблата - в среднем не больше 10х10 см, масса - не более 700 г). Корпус выполняется из ударостойкого материала. Также на парашюте нередко устанавливается автомат высоты (по конструкции — тот же высотомер), автоматически раскрывающий парашют на заданной высоте, если этого не сделал парашютист. Существуют также электронные высотомеры, они не только измеряют высоту, но и сигнализируют на заданных высотах. 3.Основные уравнения механики, используемые в динамике полета в векторной форме. 4.Системы стабилизации угловой скорости и перегрузки. Приведите примеры задач управления ЛА с применением данных систем. СТАБИЛИЗАЦИЯ И УПРАВЛЕНИЕ УГЛОВЫМ ПОЛОЖЕНИЕМ Задача автоматического управления угловым положением самолета является одной из основных задач, возникающих при пилотировании. Исторически эта задача ставилась и решалась даже раньше, чем задача автоматического демпфирования и улучшения устойчивости и управляемости самолета. Поэтому автоматические средства управления угловым положением самолета - автопилоты стали прообразами современных систем автоматического управления полетом. Автоматическое управление угловым положением осуществляется путем отклонения рулей при появлении рассогласований между текущими и требуемыми значениями угловых параметров положения самолета. Благоприятное влияние автоматики на процесс управления самолетом проявляется в улучшении качества переходных процессов возвращения самолета к исходному режиму по угловым параметрам после непроизвольного отклонения под действием внешних возмущений. Так осуществляется автоматическая стабилизация углового положения самолета. Кроме того, автоматика помогает пилоту улучшить качество переходных процессов вывода самолета на новый режим полета по угловым параметрам после целенаправленного воздействия пилота на соответствующие органы управления. Так осуществляется автоматическое управление угловым положением самолета. При автоматическом управлении угловым положением самолета приходится решать три взаимосвязанные задачи управления углами тангажа, крена и курса. Соответственно различают три основных вида средств автоматического управления угловым положением самолета: автопилоты угла тангажа, автопилоты угла крена и автопилоты курса. В последнее время задача автоматического управления углом тангажа часто решается совместно с задачей автоматического управления нормальной перегрузкой. Поэтому автопилоты нормальной перегрузки целесообразно также отнести к средствам автоматического управления угловым положением самолета. В современных системах автоматического управления автопилоты присутствуют либо в виде самостоятельных подсистем, либо в виде соответствующих режимов системы. Поэтому в дальнейшем под автопилотом будем понимать либо автономное средство, реализующее автоматическое управление угловым положением самолета, либо систему автоматического управления, работающую в режиме управления угловым положением 1.ПЗУ. Принципы организации и виды 2. .Особенности устройства указателей скорости. 1.2 Указатели скорости В самолете измеряется несколько скоростей: - VИСТ – истинная воздушная скорость - это скорость перемещения самолета относительно окружающего воздуха; - W – путевая скорость – это скорость перемещения самолета относительно земли. Путевая скорость равна векторной сумме истинной воздушной скорости и скорости ветра: где VПР – индикаторная (приборная) скорость. 1.2.1 Указатель индикаторной (приборной) скорости С подъемом на высоту плотность воздуха уменьшается и при одной и той же истинной скорости аэродинамика самолета изменяется (подъемная сила, лобовое сопротивление, критический угол атаки αКР). В связи с этим для пилотирования используют индикаторную скорость, которая характеризует скоростной напор, с которым действует воздушный поток на самолет и независимо от высоты характеризует его аэродинамику. Индикаторная скорость численно равна скорости полета относительно воздуха, которая была бы вблизи Земли с тем же скоростным напором, как и на данной высоте. При малых скоростях и небольших высотах VИСТ и VПР отличаются незначительно, поэтому на легких самолетах как правило устанавливается только указатель приборной скорости. Принцип измерения индикаторной скорости основан на измерении разницы между полным давлением набегающего воздушного потока и статическим давлением: Это следует из уравнения Бернулли для воздушного потока в области перед ПВД и внутри прибора. В соответствии с этой формулой конструкция прибора для измерения приборной скорости показана на рис. 1.15. В герметичном корпусе прибора 5 имеется манометрическая коробка 6, внутрь которой поступает полное давление из приемника воздушных давлений 1. В корпус прибора поступает статическое давление воздуха. Разница между полным и статическим давлением деформирует манометрическую коробку, подвижный центр которой через передаточный механизм перемещает стрелку прибора. Аналогичную конструкцию имеют сигнализаторы приборной скорости. Эти приборы при достижении определенного значения приборной скорости выдают сигнализацию (например, о достижении предельной скорости) или включают определенное оборудование. В сигнализаторах приборной скорости подвижный центр манометрической коробки при изменении скорости перемещает контакт, который замыкает электрическую цепь. 1.2.2 Указатели истинной воздушной скорости Уравнение Бернулли, записанное с учетом изменения плотности и сжимаемости воздуха, дает следующую зависимость между истинной воздушной скоростью VИСТ и полным и статическим давлениями: 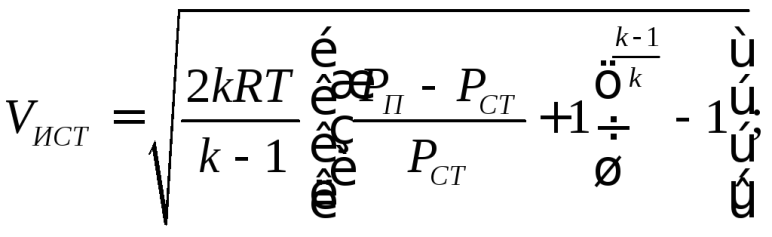 Как видно из формулы, истинная воздушная скорость является функцией температуры и отношения динамического давления к статическому давлению: 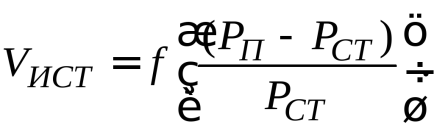 Как видно, под действием разницы между полным и статическим давлением (РПОЛ – РСТ) манометрическая коробка перемещает стрелку, и одновременно при увеличении высоты и уменьшении статического давления с высотой анероидная коробка дополнительно доворачивает стрелку. Широкое применение имеет комбинированный указатель скорости КУС-730/1100 Прибор измеряет индикаторную скорость VПР от 50 до 730 км/ч широкой стрелкой по внешней шкале и истинную скоростьVИСТ в диапазоне от 400 до 1100 км/ч по внутренней шкале. 3.Силы и моменты, действующие на летательный аппарат в полете. Силы, действующие на самолет в полете Пространственное движение самолета, характеризующееся изменением положения самолета в пространстве, изменением скорости и направления полета, называется маневром, а способность совершать маневр – маневренностью самолета (франц. manoeuvrer – приводить в движение, управлять, маневрировать, от лат. manu operor – работаю руками). Все силы, действующие на самолет в полете, могут быть сведены к трем: полной аэродинамической силе Ra , силе тяжести G и силе тяги двигателя P . Эти силы, в свою очередь, можно привести к равнодействующей силе F, приложенной в центре масс самолета, и моменту M относительно центра масс (рис. 6.4):
где
В общем случае сила F и момент M, действующие на самолет, отличны от нуля и самолет движется поступательно вдоль вектора силы F с ускорением j = F/m и вращается относительно оси, направленной вдоль вектора M с угловым ускорением
где
Момент инерции самолета относительно центра масс
где
Движущийся в криволинейном пространственном полете самолет можно рассматривать как находящийся в равновесии, если попринципу Д'Аламбера (по имени французского математика, механика и философа Ж. Л. Д'Аламбера) включить в число действующих на него сил силу инерции
равную сумме инерционных сил, действующих на каждый агрегат самолета. Таким образом, можно записать: F + Pj = 0, т.е.Ra + G + P + Pj = 0. Все силы, действующие на самолет в полете, удобно объединить в две группы: - поверхностные силы - силы, не связанные с массой самолета (полная аэродинамическая сила Ra и сила тяги двигателя P ), которые, собственно, и определяют полет: Rп= Ra + P ; - массовые силы – силы, связанные с массой самолета (сила тяжести G и инерционная сила Pj ), которые необходимо преодолеть для совершения полета: Rм = G + Pj. Здесь уместно еще раз отметить, что сила лобового сопротивления Xa, которую приходится преодолевать силой тяги двигателя P, возникает как неизбежное следствие получения подъемной силы Ya, неразрывно связана с ней, поэтому силу лобового сопротивления, как и подъемную силу, с полным основанием можно отнести к группе силRп, которые определяют полет. Таким образом, можно рассматривать равновесие самолета в любом пространственном движении под действием сил Rп и Rм, т. е. F = Rп + Rм = 0; M = Mп + Mм = 0. Изменение силы F и момента M(появление приращенийΔFи ΔM при изменении полной аэродинамической силы Ra, силы тяги двигателя P или силы тяжести G) приводит к изменению параметров пространственного движения самолета.Движение самолета неуправляемое, если приращения (возмущения) силы ΔFи момента ΔMне обусловлены действиями летчика, а вызваны какими- либо не зависящими от него обстоятельствами (например, порыв ветра в турбулентной атмосфере). Движение самолета управляемое, если приращение силы ΔF и момента ΔMобусловлено действиями летчика. В этом случае ΔFи ΔMназываются управляющими воздействиями. Летчик может изменить значение и ориентацию в пространстве полной аэродинамической силы, значение и направление силы тяги двигателя. Целенаправленное изменение этих сил приведет к формированию потребной траектории полета самолета. При решении многих задач, связанных с полетом самолета (расчет траекторий, определение прочностных характеристик и т. д.), используется понятие перегрузки. Перегрузка– отношение суммы векторов полной аэродинамической силы и силы тяги к силе тяжести:
Поскольку Rп = Ra + Pи P = – Pм , то
Вектор перегрузки характеризует маневренность самолета, так как он учитывает величину и направление сил, изменяя которые можно управлять траекторией движения самолета. Перегрузка показывает, во сколько раз силы, определяющие траекторию движения, больше или меньше силы тяжести самолета или (что то же самое) во сколько раз ускорение движения самолета в каком-либо направлении больше или меньше ускорения земного тяготения. Для каждого отдельно взятого агрегата самолета или любого груза, находящегося на самолете, перегрузка показывает, во сколько раз действующая на него сила больше или меньше силы тяжести агрегата или груза. Перегрузка, действующая на самолет, может быть записана через ее проекции nx, ny, nz, на оси координат в виде
где
4.Управление центром масс самолета. Задачи, методы и назначение систем стабилизации высоты и скорости полета. Система стабилизации скорости воздействием на тягу двигателей, на руль высоты. Совместная стабилизация высоты и скорости полета. |