Математика. Вариант 4, Математика. Контрольная работа 2 Задача Найти общее решение дифференциального уравнения с разделяющимися переменными. Решение
 Скачать 147.33 Kb. Скачать 147.33 Kb.
|
|
Вариант 4 Контрольная работа №2 Задача 1. Найти общее решение дифференциального уравнения с разделяющимися переменными. 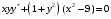 Решение 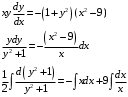 Таким образом, общее решение исходного дифференциального уравнения имеет вид: 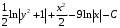 . .Задача 2. Найти общее решение однородного дифференциального уравнения.  Решение 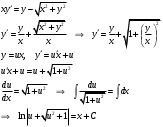 Тогда, искомое общее решение: 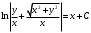 . .Задача 3. Найти, применяя подстановку Бернулли, общее решение линейного дифференциального уравнения первого порядка. 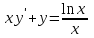 Решение 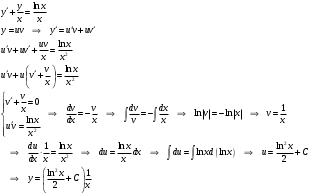 Таким образом, общее решение имеет вид: 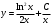 . .Задача 4. Найти общее решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами. 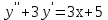 Решение Будем искать решение в виде суммы 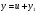 , где , где  - решение соответствующего однородного уравнения, а - решение соответствующего однородного уравнения, а 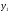 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения.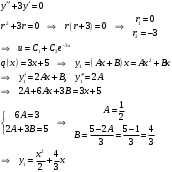 Окончательно получаем: 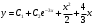 . .Задача 5. Исследовать сходимость положительного ряда, применяя какой–либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный): a) 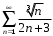 ; b) ; b) 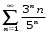 ; c) ; c) . . Решение 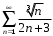 Сравним исходный ряд с обобщённым гармоническим рядом 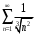 , который сходится, поскольку показатель степени его знаменателя , который сходится, поскольку показатель степени его знаменателя  . .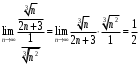 Получено конечное, отличное от нуля число, значит исследуемый ряд сходится, как и ряд 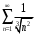 , согласно предельному признаку сравнения. , согласно предельному признаку сравнения.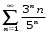 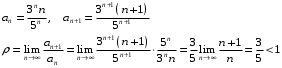 Следовательно, данный ряд сходится по признаку Даламбера.  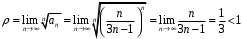 Следовательно, ряд сходится по радикальному признаку Коши. Задача 6. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости: 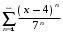 Решение 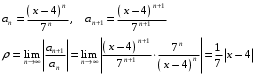 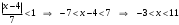 - интервал сходимости ряда - интервал сходимости рядаПри 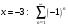 При 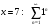 Оба эти ряда расходятся, т.к. не выполняется необходимый признак сходимости ряда. Таким образом, искомая область сходимости: 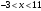 . .Задача 7.(Комбинаторный метод вычисления вероятностей в классической схеме). Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5. Решение Пусть событие А – извлекли жетон, не содержащий цифру 5 Общее число всех возможных элементарных исходов 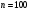 Число не благоприятствующих исходов – 19 (5,15,25,35,45,65,75,85,95,50,59,51,52,53,54,55,56,57,58) 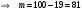 - число благоприятствующих исходов - число благоприятствующих исходов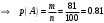 Задача 8. (Формула полной вероятности и формула Байеса) 4. На сборку поступают детали с трех конвейеров. Первый дает 25%, второй – 30% и третий – 45% деталей, поступающих на сборку. С первого конвейера в среднем поступает 2% брака, со второго – 3%, с третьего – 1%. Найти вероятность того, что: а) на сборку поступила бракованная деталь; б) поступившая на сборку бракованная деталь – со второго конвейера. Решение Событие А – на сборку поступила бракованная деталь В1 – деталь сделана на 1-ом заводе В2 – деталь сделана на 2-ом заводе В3– деталь сделана на 3-тьем заводе 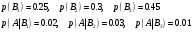 а) 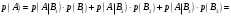 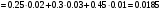 б) 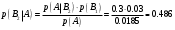 . .Задание 9. Выборка, её числовые характеристики Для указанных ниже статистических распределений выборок требуется: 1) Найти эмпирическую функцию распределения и построить ее график. 2) Построить полигон частот. 3) Вычислить выборочную среднюю. 4) Вычислить выборочную и исправленную дисперсии. xi -2 1 2 3 4 5 ni 2 1 2 2 2 1 Решение. 1). Объём выборки. 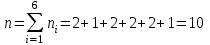 эмпирическая функция 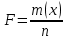 , где , где 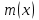 - суммарное число выборочных значений тех частот, аргументы которых удовлетворяют неравенству - суммарное число выборочных значений тех частот, аргументы которых удовлетворяют неравенству 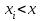 . .Поэтому 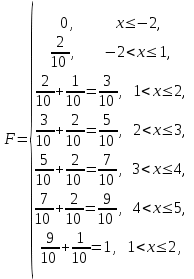 или 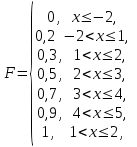 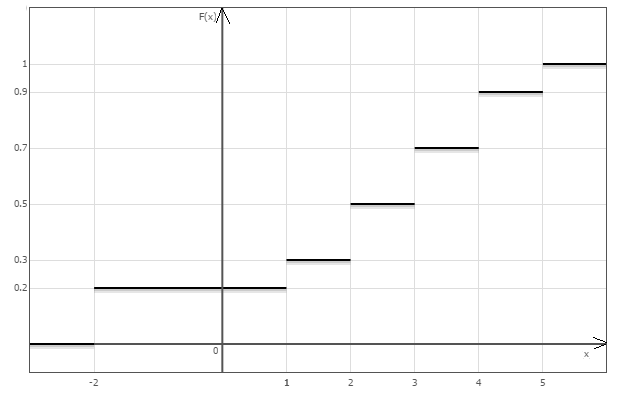 2). Полигон частот (для дискретной случайной величины) – ломанная, соединяющая точки 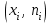 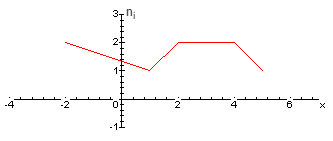 3). Найдём теперь выборочное среднее 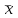 по следующей формуле по следующей формуле 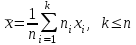 . .В данном случае число групп данных 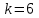 , поэтому выборочное среднее равно , поэтому выборочное среднее равно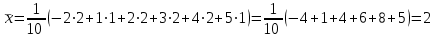 4). Теперь найдём выборочную дисперсию по следующей формуле 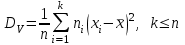 или 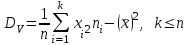 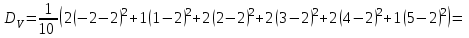 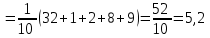 . .Найдём теперь исправленную дисперсию по следующей формуле 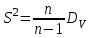 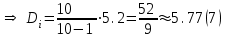 . .Задание 10. Доверительные интервалы для параметров нормального закона распределения Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью  = 0,95, зная выборочную среднюю = 0,95, зная выборочную среднюю 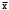 , объем выборки n и среднее квадратичное отклонение , объем выборки n и среднее квадратичное отклонение  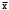 = 75,14; n = 81; = 75,14; n = 81;  Решение. Доверительный интервал вычисляется по следующей формуле 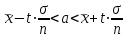 По таблице для функции Лапласа найдём значение 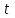 из равенства из равенства 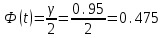 . .По полученному значению 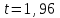 определим точность оценки (или половину длины доверительного интервала) определим точность оценки (или половину длины доверительного интервала) 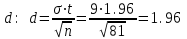 . Отсюда получаем искомый доверительный интервал . Отсюда получаем искомый доверительный интервал 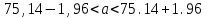 или или 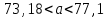 . . |
