вариант 1. Контрольная работа по дисциплине Техническая механика по специальности 13. 02. 11. Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (в отрасли машиностроения)
 Скачать 173.47 Kb. Скачать 173.47 Kb.
|
|
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ ГОБПОУ «ЛИПЕЦКИЙ МАШИНОСТРОИТЕЛЬНЫЙ КОЛЛЕДЖ» КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Техническая механика» по специальности 13.02.11. «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (в отрасли машиностроения)» Nв = 1 Выполнил: Студент гр. ЭЗ-21 Беляева Т.В. Проверила: Болховитинова Г.Ю. Липецк 2021 Содержание1Содержание дисциплины. Разделы «Технической механики». 3 2 Плоская система произвольно расположенных сил. Приведение Плоской системы произвольно расположенных сил к точке. 4 3 Простейшие движения твёрдого тела. 5 4 Раздел «Сопротивление материалов». Метод сечений. 6 5 Деформация кручение. Определение крутящего момента и построение эпюр крутящих моментов. 9 Список использованной литературы 11 Содержание дисциплины. Разделы «Технической механики».Дисциплина «Техническая механика» является общепрофессиональной дисциплиной и предназначена для подготовки специалистов базового и повышенного уровня на всех технических специальностях. Техническая механика – комплексная дисциплина. Техническая механика — это общетехническая дисциплина, в которой излагаются основы и методика расчета наиболее распространенных элементов различных конструкций на прочность, жесткость и устойчивость. Дисциплина «Техническая механика» является общепрофессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем. "Техническая механика" - собирательное название, обычно включающее в себя дисциплины "Теоретическая механика", "Сопротивление материалов", и "Детали машин". Целью изучения дисциплины является рассмотрение предмета технической механики, методов и приемов технической механики, форм и видов расчетов по технической механике, постановки и решения прикладных задач. Она включает три раздела: «Теоретическая механика», «Сопротивление материалов», «Детали машин». «Теоретическая механика» - раздел, в котором излагаются основные законы движения твердых тел, и их взаимодействия. Теоретическая механика имеет следующие разделы: статика, кинематика и динамика. Статика-это раздел механики, который изучает равновесие механических систем под воздействием внешних сил и вращающих моментов. Кинематика изучает математическое описание движения объектов. Динамика - раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчетов элементов конструкций на прочность, жесткость и устойчивость под действием» внешних сил. «Сопротивление материалов» изучает теорию расчета оптимальных размеров отдельных элементов сооружений и машин на прочность и устойчивость, что обеспечивает надежность их работы при заданной нагрузке. Сопротивление материалов развивается на основе обобщения опыта работы построенных сооружений и экспериментального изучения усилий и деформаций на моделях сооружений в лабораторных условиях. Раздел «Детали машин» изучает теорию расчета и принципы конструирования отдельных элементов и простейших соединений машин. 2 Плоская система произвольно расположенных сил. Приведение Плоской системы произвольно расположенных сил к точке.Плоская система произвольно расположенных сил — это система сил, линии действия которых расположены в одной плоскости произвольным образом. Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему следует упростить. Для этого все силы системы переносят в одну произвольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил. Рассмотрим случай переноса силы в произвольную точку, не лежащую на линии действия силы. Теорема. Действие силы на тело не изменится, если ее перенести параллельно самой себе в любую точку тела, присоединяя при этом некоторую пару сил. Доказательство. Пусть к телу в некоторой точке К приложена сила F (рис.1). Перенесем в произвольную точку О того же тела силу F = F' параллельно данной силе. Но чтобы равновесие не изменилось, к точке О надо приложить равную по величиной противоположно направленную_силу F" (см. рис. 1.).  Рисунок 1- Перенос силы в произвольную точку Силы F' и F" взаимно уравновешиваются, и поэтому действие на тело одной данной силы F эквивалентно действию на него системы трех сил F, F' и F". При этом сила F' может рассматриваться как сила F, перенесенная параллельно своему начальному направлению в точку О, а силы F" и F образуют пару, которую мы должны присоединить при параллельном переносе силы из точки К в точку О, чтобы сохранить действие силы при этом переносе. Теорема доказана. Пару (F" F), образующуюся при переносе точки приложения силы F, называют присоединенной парой. 3 Простейшие движения твёрдого тела.К простейшим движениям твердого тела относится поступательное и вращательное движение (см. рис.2 и 3). Поступательное движение твердого тела —это такое движение, при котором прямая, проведенная в теле между любыми двумя точками, перемещается параллельно самой себе.  Рисунок 2 - Поступательное движение твердого тела При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс. При поступательном движении все точки тела имеют одинаковые скорости, одинаковые ускорения и проходят одинаковые отрезки пути. Вращательным движением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям, лежащим в плоскостях, перпендикулярных оси вращения, с центрами на этой оси.  Рисунок 3 - Вращательным движением твердого тела Работа большинства машин и механизмов основана на вращательном движении. 4 Раздел «Сопротивление материалов». Метод сечений.Сопротивление материалов - наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и деталей машин. Элементы сооружений отличаются друг от друга формами, размерами, материалом, функциональным назначением, рядом специальных требований. При этом следует отметить, что все без исключения элементы как искусственного, так и естественного происхождения обладают такими свойствами, как прочность и жесткость, то есть способностью, не разрушаясь воспринимать различные нагрузки и сопротивляться изменению своих первоначальных форм и размеров, без чего не может нормально функционировать сооружение. Цель расчетов в сопротивлении материалов – создание прочных, устойчивых, обладающих достаточной жесткостью, долговечностью и вместе с тем экономичных элементов сооружений Метод сечений — это прием, позволяющий обнаруживать внутренние силы и рассматривать их как внешние силы по отношению к оставшейся (рассматриваемой) части тела. Метод сечений (иногда его называют РОЗУ) — наиболее удобный способ определения внутренних силовых факторов для построения их эпюр, который рассматривает равновесие отсеченных частей бруса. Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить. Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил. Очевидно, что, согласно третьему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Поэтому, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще. В соответствии с принятым допущением о непрерывности материала тела мы можем утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению. Применяя к оставленной части тела условия равновесия, мы не сможем найти закон распределения внутренних сил по сечению, но сможем определить статические эквиваленты этих сил. Так как основным расчетным объектом в сопротивлении материалов является брус и чаще всего нас будут интересовать внутренние силы в его поперечном сечении, то рассмотрим, каковы будут статические эквиваленты внутренних сил в поперечном сечении бруса. Рассечем брус (рис. 4) поперечным сечением а — а и рассмотрим равновесие его левой части. 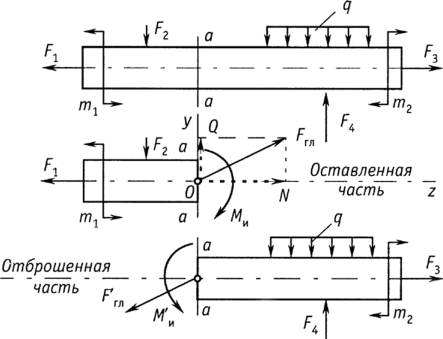 Рисунок 4 – Метод сечений Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а — а, будут главный вектор Fm, приложенный в центре тяжести сечения, и главный момент МТЛ — МИ, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса. Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси, то есть лежащую в плоскости поперечного сечения. Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую N назовем продольной силой, составляющую Q — поперечной силой, а пару сил с моментом Мк — изгибающим моментом. Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно: (ось z всегда направляем по оси бруса). Если внешние силы, действующие на брус, не лежат в одной плоскости, то есть представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 5), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:  Рисунок 5 – Внутренние силовые факторы Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N — продольная сила, Qx, Qy— поперечные силы, Мк — крутящий момент, Мш, Миу— изгибающие моменты. 5 Деформация кручение. Определение крутящего момента и построение эпюр крутящих моментов.Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют. Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рисунок ). Деформациям кручения подвергаются валы и пружины. Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.  Рисунок 6 – Деформация кручение Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент Мк в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала. Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 7).  Рисунок 7 – Правило знаков для крутящего момента Общий порядок расчета и построения эпюры. Намечаем характерные сечения стержня. Определяем крутящий момент в каждом характерном сечении. По найденным значениям моментов строим эпюру. При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз. Крутящий момент для сечения можно выразить так:   Рисунок 8 – Определение крутящего момента Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид:  где Lmн и Lmк – расстояние от начала координат до начала и до конца распределенного момента соответственно. Список использованной литературыБутенин, Н.В. и др. Курс теоретической механики: Учеб.пособие для студентов вузов по техн.спец.:В 2-х т. / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. СПб.: Лань.-5-е изд., испр.-2017. -729 с. Вереина, Л.И. Техническая механика: Учебник / Л.И. Вереина. - М.: Academia, 2018. - 316 c. Михайлов, А.М. Техническая механика: Учебник / А.М. Михайлов. - М.: Инфра-М, 2018. - 160 c. Сафонова, Г.Г. Техническая механика: Учебник / Г.Г. Сафонова, Т.Ю. Артюховская, Д.А. Ермаков. - М.: Инфра-М, 2017. - 400 c. Эрдеди, А.А. Техническая механика: Учебник / А.А. Эрдеди. - М.: Academia, 2018. - 112 c. |
