Лабораторная работа 1. Лабораторная работа 1 определение плотности твердого тела
 Скачать 0.8 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1 ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛАПриборы и принадлежности: цилиндр, технические весы, разновесы, штангенциркуль Цель работы: освоить расчет ошибок косвенных измерений на примере определения плотности тела. ТЕОРИЯ. Выполнение лабораторных работ связано с измерением различного рода физических величин. Измерение-это процесс сравнения измеряемой величины с однородной ей величиной, принятой за единицу меры. Вследствие несовершенства наших органов чувств и измерительных приборов измерения выполняются с ограниченной степенью точности, т. е. значение измеряемой величины отличается от истинного. Под степенью точности прибора понимается та наименьшая часть единицы меры, до которой с уверенностью в правильности результата может быть проведено измерение (например, степень точности школьной линейки 1 мм). Ошибки (погрешности), возникающие при измерении, делятся на два больших класса: систематические и случайные. Систематические ошибки- ошибки, сохраняющие свою величину и знак от измерения к измерению. Они связаны с неисправностью прибора, неудачно выбранным методом измерений и т. д. Так как систематические ошибки постоянны, то они не поддаются математическому анализу, но их можно выявить и устранить. Случайные ошибки- ошибки, которые непредсказуемым образом изменяют свою величину (и знак) от измерения к измерению. Они являются следствием несовершенства наших органов чувств, действия факторов, влияние которых невозможно учесть, и т. д. Устранить их нельзя, но они подчиняются статистическим закономерностям, их можно рассчитать, используя методы математической статистики. Величина случайной ошибки существенно уменьшается при увеличении числа измерений. Измерения делятся на два вида: прямые и косвенные. Прямые измерения- измерения, при которых числовые значения искомой величины получаются непосредственным сравнением ее с единицей меры.  Косвенные измерения- измерения, при которых значения искомой величины находятся по результатам измерений других величин, связанных с этой величиной определенной функциональной зависимостью. Расчет ошибок прямого измерения. Пусть проведено n измерений некоторой величины Х. В результате получен ряд значений этой величины:  Наиболее вероятным является среднее арифметическое значение этой величины  : = где i=1,2,3,…,n Величина  называется абсолютной погрешностью отдельного измерения.Средней арифметической погрешностью  называют среднее арифметическое значение абсолютных погрешностей отдельных измерений: Средняя арифметическая определяет интервал  , внутри которого находится истинное значение измеряемой величины Х.Качество результата измерений характеризуют средней относительной погрешностью. Средней относительной погрешностью  называют отношение средней арифметической погрешности к среднему значению измеряемой величины : Для более точного расчета абсолютной погрешности используют суммарную погрешность  Суммарная погрешность 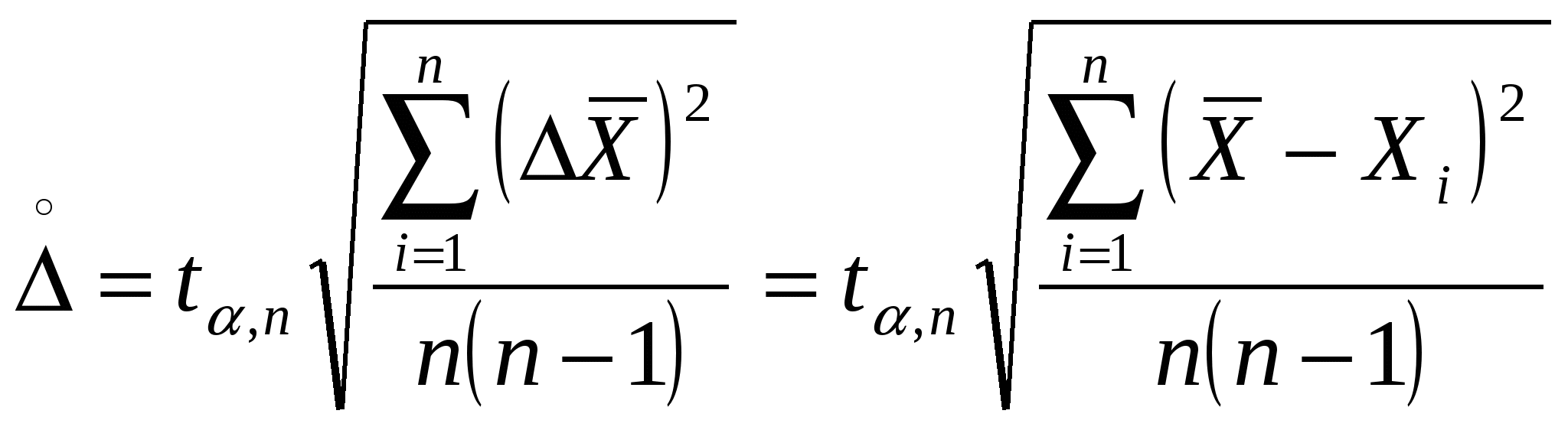учитывает случайную погрешность  , погрешность прибора  , погрешность округления  и определяется соотношением: , (1)где определяют по формуле Стьюдента: ,t  - коэффициент Стьюдента (берется из таблицы Стьюдента),n- число измерений;  , где  - предельная ошибка прибора, указанная в паспорте. , где  - наименьшее деление прибора.РАСЧЕТ ОШИБОК КОСВЕННОГО ИЗМЕРЕНИЯ Пусть искомая величина Z является функцией двух переменных X и Y, т.е Z=f(x, y). Установлено, что абсолютная ошибка функции y=f(x) равна произведению производной этой функции на абсолютную ошибку аргумента, т. е.  . Поэтому для определения абсолютной ошибки функции Z= f(x,y) находят полный дифференциал этой функции: dz=  , (2)где  и  -частные производные функции Z по аргументам X и Y.Каждая частная производная находится как простая производная функции Z=f(x,y) по соответствующему аргументу, если оставшийся аргумент рассматривать как постоянный множитель. При малых значениях дифференциалов аргументов dx и dy (или приращений аргументов  и  ) приращение функции  .В этом случае формула (2) принимает вид:  Z= .В качестве средней абсолютной погрешности принимают среднюю квадратичную погрешность  ,которая определяется соотношением: , (3)где  и  -суммарные погрешности измерений величины X и Y, определяемые по формуле (1).Средняя относительная погрешность величины Z рассчитывается по формуле  . Следовательно, разделив обе части выражения (3) на  , получим относительную погрешность функции Z: Зная относительную погрешность, находят абсолютную ошибку величины Z:  Окончательный результат измерений записывают так: Z=  .Рассмотрим расчет ошибок на примере определения плотности твердого тела правильной геометрической формы. Для цилиндра массой m, высотой h, диаметром D средняя плотность определяется соотношением:  .Используя формулу (3), для нашего случая получаем:  .Найдя частные производные  имеем: . Разделив левую и правую часть последнего выражения на  ,получаем:  ,отсюда Таким образом, относительная погрешность плотности  .Зная относительную ошибку, находим абсолютную погрешность плотности (  ): .Окончательный результат запишем так:  При обработке результатов измерений следует помнить, что точность вычислений должна быть согласована с точностью самих измерений. Например, если хотя бы одна из величин в каком-либо выражении определена с точностью до двух значащих цифр, то нет смысла вести вычисление результата с точностью большей двух значащих цифр. Для уточнения последней значащей цифры результата нужно вычислить следующую за ней цифру: если она окажется меньше 5, то ее следует просто отбросить; если она больше 5 или равна 5,то отбросив ее, следует предыдущую цифру увеличить на единицу. Вычисление погрешности измерений производят с такой же точностью, что и вычисление самой измеряемой величины. Например: Правильно. Неправильно. Z= 284  Z= 284,5 Z= 52,7  Z=52.74 Z= 4,750  Z=4,75 ОПИСАНИЕ ПРИБОРОВ 1.Штангенциркуль. Штангенциркули бывают различной формы и неодинаковой точности. Чаще всего они представляют собой Т-образную масштабную линейку (рис.1), вдоль которой свободно передвигается меньшая линеечка-нониус. 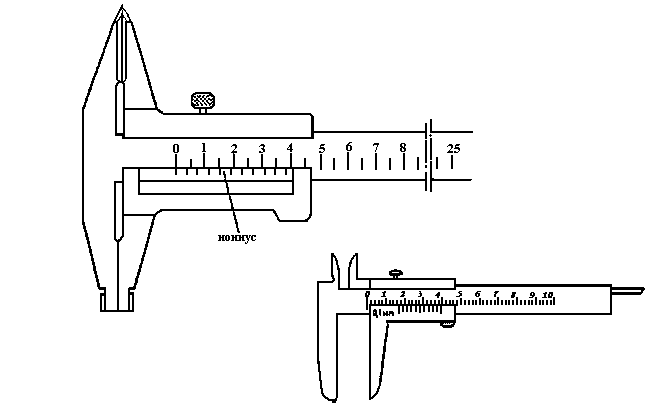  Рис.1 Т Т-образная масштабная линейка -образные ветви линеечек, или “ножки” штангенциркуля служат для контакта с измеряемым телом. Нижние их концы предназначены для измерения наружных размеров тел, а верхние- внутренних (например, внутреннего диаметра трубки). Подвижная линейка имеет прорез, через который видны деления масштабной линейки. На нижней, скошенной кромке прореза нанесены деления нониуса. Нониус служит для более точного отсчета долей масштаба. Масштабная линейка разделена на см и мм. Рассмотрим штангенциркуль с точность измерения 0,1 мм. Деление нониуса такого штангенциркуля на 0,1 мм короче деления масштабной линейки, т. е. в 10 делениях нониуса укладывается 9 делений масштаба. Т. о. цена наименьшего деления прибора 0,1 мм. При плотно сомкнутых “ножках” штангенциркуля нуль нониуса и нуль масштаба совпадают (рис. 2, положение 1). Для измерения линейного размера тела его помещают между “ножками” штангенциркуля так, чтобы соприкосновение “ножек” с телом было полным, но не вызывало бы деформации. В этом случае расстояние между нулевыми штрихами масштаба и нониуса соответствует размеру измеряемой величины. Рассмотрим два примера:
Нулевое деление нониуса не совпадает ни с одним делением масштаба (рис.2, положение 3). Смотрят, какое деление масштаба прошел нуль нониуса (например, третье), затем, какой из штрихов нониуса совместился (составляет одну прямую) с каким-либо штрихом масштаба. На нашем рисунке седьмой штрих нониуса совпадает с десятым делением масштаба. Так как цена наименьшего деления данного штангенциркуля (точность прибора) 0,1 мм, то седьмой штрих нониуса соответствует 0,7 мм. Следовательно, длина измеряемого тела равна 3 мм + 0,7 мм = 3,7 мм. Имеются штангенциркули с точностью 0,05 мм. Цена наименьшего деления указывается на штангенциркуле. 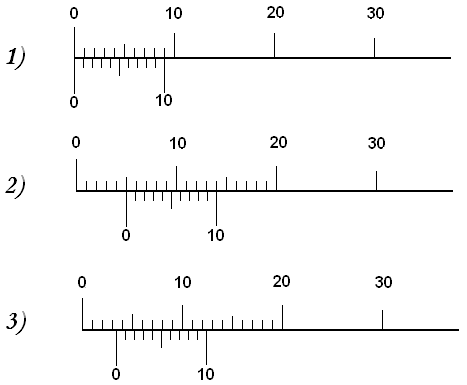 При раздвижении “ножек” штангенциркуля с конца масштабной линейки выдвигается игла. Длина ее соответствует расстоянию между нулевыми штрихами нониуса и шкалы масштаба, поэтому игла может быть использована как измеритель глубины отверстия, трубки и т. д. Рис.2
В данной работе используются технические весы. Приступая к взвешиванию, необходимо соблюдать следующие правила: 1. Проверить исправность весов: а) весы должны быть в равновесии (какая-либо чашка не должна перевешивать); б) стрелка указателя при качании коромысла не должна задевать шкалу с делениями. 2. Нагружать весы взвешиваемым телом или разновесами, а так же снимать их с чашки весов можно только при арретированных весах. Арретир- приспособление, позволяющее класть коромысло весов на опоры, предохраняющие призмы весов от износа.
Порядок выполнения работы
(Измерение одного размера провести 5 раз).
Таблица
 = ,где Х1, Х2,…, Хn – измеренные значения величины; n- число измерений. 5. Определить среднее значение плотности:  6. Вычислить относительную погрешность плотности:  (4)а) Найти суммарную ошибку  с учетом ошибки прибора и ошибки округления ( =0, т. к. измерение однократное):  .Для технических весов   отсюда = 0,05(г).б) Вычислить суммарную ошибку  по формуле (1):  ,где  .Из таблицы Стьюдента для рекомендуемой надежности  = 0,95 и количестве измерений n=5 находится коэффициент Стьюдента  .в) Аналогично найти суммарную ошибку  :  , где 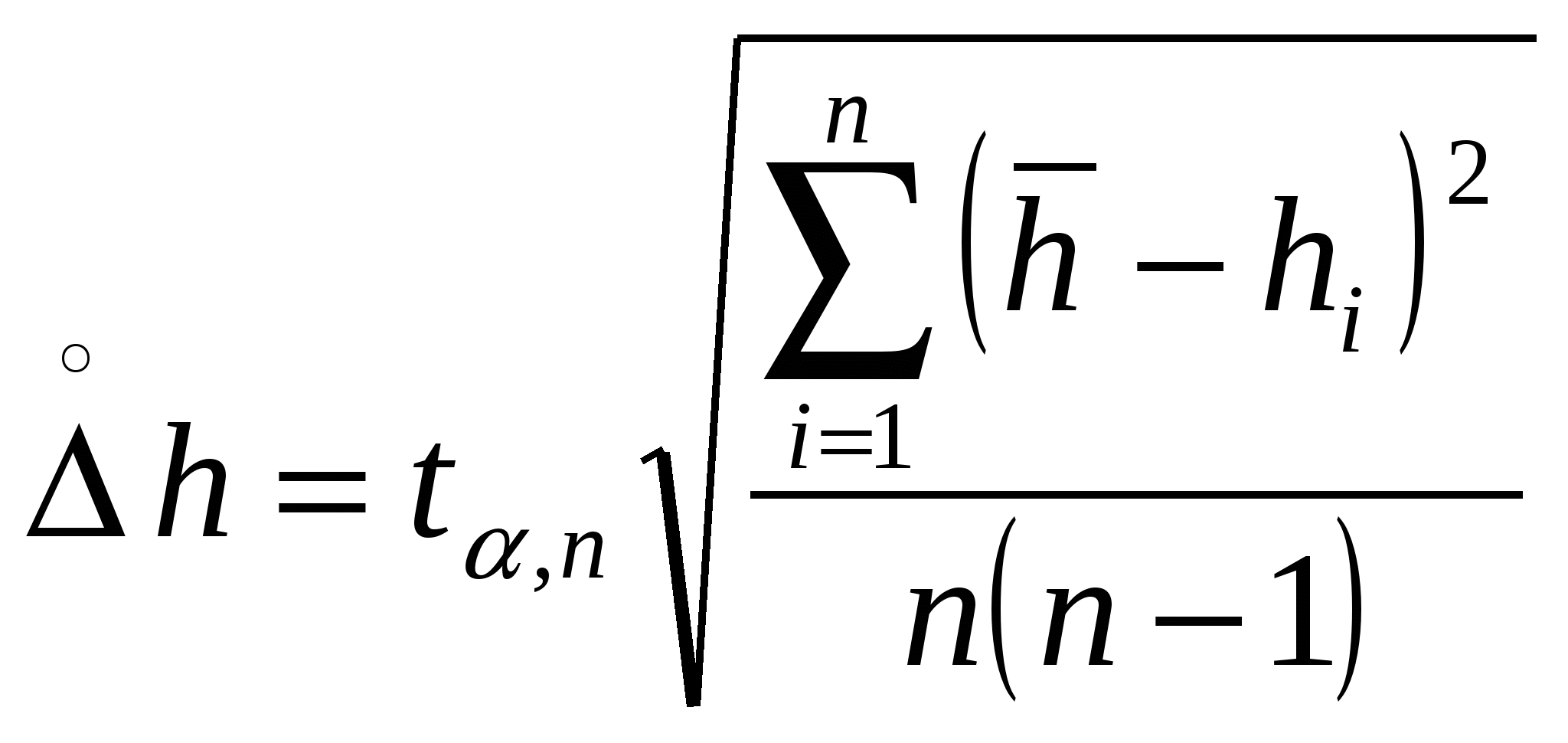 .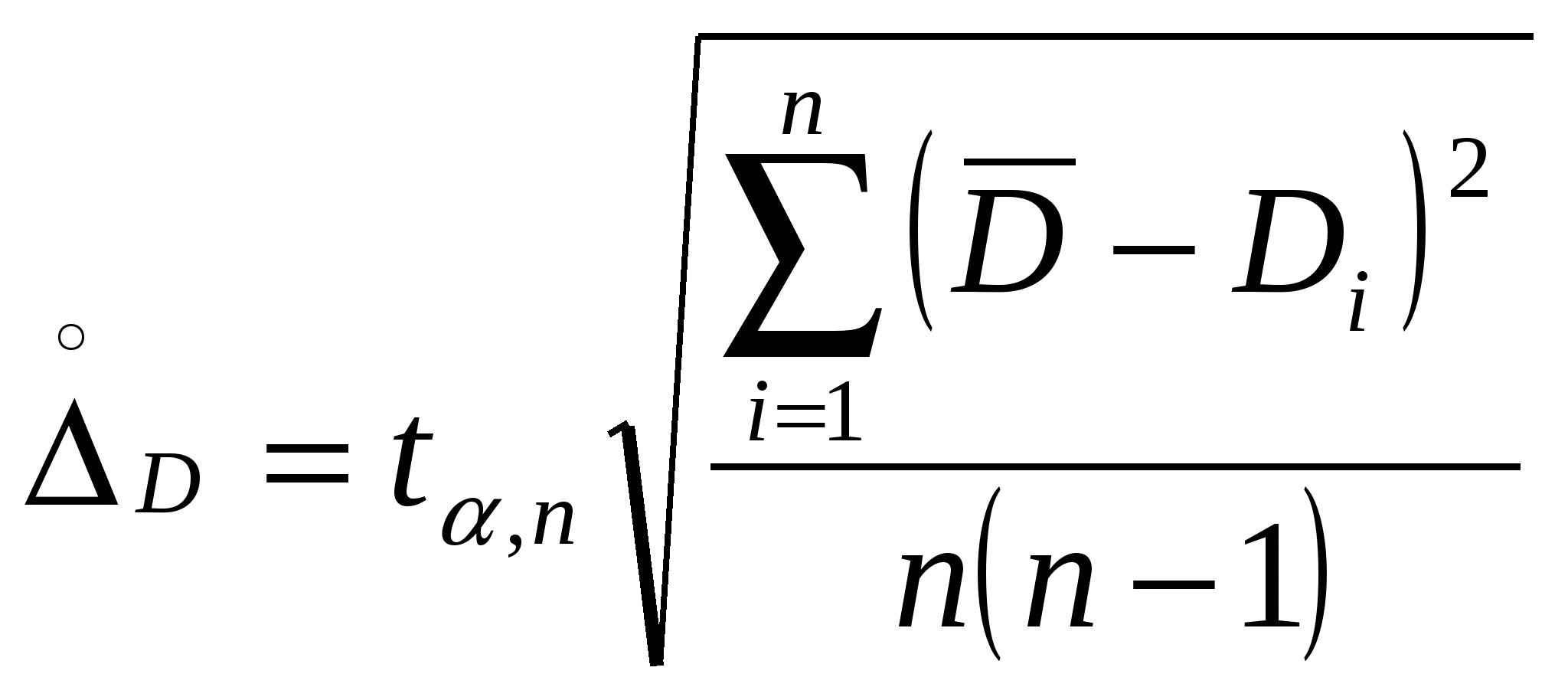ПРИМЕЧАНИЕ. Если и не превышают 0,5 ,то ими можно пренебречь, т. к. точность расчета не должна превышать точность прибора.г) Вычислить относительную погрешность по формуле (4).7. Найти абсолютную погрешность плотности: 8. Записать окончательный результат в виде:  КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что понимается под степенью точности прибора? 2 .Какие ошибки называются систематическими? 3. Что такое случайные ошибки? 4. Какие измерения называют прямыми? 5. Какие измерения называют косвенными? 6. Записать формулу для расчета среднего арифметического значения. 7. Записать формулу для расчета средней арифметической погрешности. 8. Записать формулу для расчета средней относительной погрешности. 9. Записать формулу для расчета суммарной погрешности  .10. Как определить число значащих цифр? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
