Лекция 3инарные отношения и их свойства Декартово произведение Декартовым произведением двух множеств

• Название: Лекция 3инарные отношения и их свойства Декартово произведение Декартовым произведением двух множеств
• Дата: 21.09.2021
• Размер: 221 Kb.
• Имя файла: lektsia_3.doc
• Тип: Лекция; #234850

Дискретная математика: Математическая логика

Лекция 3инарные отношения и их свойства

Декартово произведение

Декартовым произведением двух множеств Aи B является новое множество C, элементами которого являются все упорядоченные пары (a,b), . Порядок в паре очень важен, в общем виде .

Выбирая различные подмножества декартова произведения, мы приходим к понятиям бинарного отношения, операции и функции.

Бинарное отношение

Бинарным отношением Т(М) на множестве М называется подмножество . Довольно часто используется другая, инфиксная форма записи бинарного отношения aTb = .

Мы уже стакивались с понятием отношения при рассмотрении (включение) и = (равенство) между множествами. Так же неоднократно вами использовались отношения , заданные на множестве чисел как натуральных, так и целых, рациональных, вещественных и т.д.

Определим несколько понятий относительно отношения [1]:

Обратное отношение ;

Дополнительное отношение ;

Тождественное отношение ;

Универсальное отношение ;

Обобщая понятие бинарного отношения, введем n-арное отношение, как множество упорядоченных кортежей (наборов), являющегося подмножеством n-арного декартового произведения


Задача 1

На множестве M1= {a, b, c, d, e, f} построить тождественное бинарное отношение U.

Решение

По определению, на множестве M1= {a, b, c, d, e, f} тождественное бинарное отношение U={(a,a), (b,b), (c,c), (d,d), (e,e), (d,d)}.
Задача 2
На множестве M натуральных чисел от 1 до 5 построить бинарное отношение R={(a,b)/mod(a,b)=0}.

Решение

В соответствии с заданием, на множестве натуральных чисел Mстроим такиепары (a, b), что, аделится на b без остатка (mod(a,b)=0). Получаем R={(1,1), (2,2), (3,3), (4,4), (5,5), (2,1), (3,1), (4,1), (5,1), (4,2)}.
Бинарное отношение F декартова произведения XY называется функцией, если для каждого элемента найдется не более одного элемента такого, что (x, y), т.е. выполняется свойство однозначности полученного результата;

Множество Xназывается областью определения функции Dom, и множество Y, область значений функции. Если элемент , то говорят, что функция Fне определена на z. Таким образом, функции могут быть полностью определенными на множестве X, так и частично определенными. Точно также, область значений функции может не совпадать с множеством Y, а быть его подмножеством.

Если область определения функции F из X в Y совпадает с X, то пишут F: X →Y.

Пример: тождественная функция U переводит множество X само в себя, причем U: X →X. для любого . А функция константы С, полностью определенная на Х, переводит все элементы множества Х в один единственный элемент , С: X →у.₀

Для функций, обычно, вместо записи или xFy, используют y=F(x).

Функция называется F: X →Y инъективной, или инъекцией, или вложением, если она переводит разные элементы в разные, то есть .

Функция F: X → Y называется сюръективной, или сюръекцией, или наложением, если множество ее значений есть все Y, т.е. .

Иногда такие функции называют отображениями на Y.

Функция F: X →Y называется биекцией или взаимно однозначным соответствием, если она одновременно является инъекцией и сюръекцией (вложением и наложением),

Если F - биекция, то существует обратная функция F^-1, для которой тогда и только тогда, когда .

Частным случаем функции является операция О. В этом случае область значения Х и область определения Y совпадают, т.е. .

Задача 3

Построить на множестве M={a, b, c, d} отношение, сюръекцию, инъекцию и биекцию максимальной мощности.

Решение

Отношение максимальной мощности совпадает с декартовым произведением и его мощность равна 16.

При построение инъекции необходимо учитывать, что разным х соответствуют разные у, например F1={(a, b), (b, c), (c,d), (d,a)}, Для построения сюръекции нужно использовать все элементы у, F2={(a,a), (b,d), (c,c), (d,b)}. Обе эти функции являются как сюръекциями, так и инъекциями, следовательно, они – биекции. Мощность во всех случаях равна четырем.

Сами решения могут быть и другие, но максимальная мощность вычисляется однозначно.

Декартово произведение, отношение, функция или операция могут быть и n-арные.

Способы задания бинарных отношений

Бинарные отношения R можно задать:

• 
  Перечислением, как любое множество пар,
  
• 
  Графически, когда каждый элемент х множества М представляется вершиной, а пара представляется дугой из х в у;
  
• 
  Матричным способом, с помощью матрицы смежности или матрицы инцинденций (инциндентности);
  
• 
  Фактор-множеством.
  

Перечисление элементов бинарного отношения мы использовали при решении задач №1 и №2. Построим графическое решение задачи 2 (рис.1).

	1	2	3	4	5
1	1	0	0	0	0
2	1	1	0	0	0
3	1	0	1	0	0
4	1	1	0	1	0
5	1	0	0	0	1

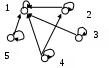Рис.1. Графическое решение задачи № 2Рис. 2. Матрица смежности

Матрица смежности S представляет собой квадратную матрицу , и каждый ее элемент

На рис. 2 представлена матрица смежности решения задачи № 2.

Для определения фактор-множества необходимо определить окрестность единичного радиуса , состоящей из таких , что .

Фактор-множество R/M множества М по отношению к R называется множество окрестностей единичного радиуса для всех элементов М при заданном R. На рис.3 решение задачи № 2 представлено в виде фактор-множества.

1 R/M=	2	3	4	5
{1}	{1, 2}	{1, 3}	{1, 2, 4}	{1, 5}

Рис. 3. Фактор-множество

Свойства бинарных отношений

Бинарное отношение T(M) называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) принадлежит этому бинарному отношению, т.е. .

Классическим определением этого свойства является утверждение:



Прямо противоположное свойство бинарных отношений называется иррефлексивностью. Бинарное отношение T(M) называется иррефлексивным тогда и только тогда, когда для каждого элемента пара (x,x) не принадлежит этому бинарному отношению, т.е. .

Классическим определением свойства иррефлексивности является утверждение:



Если бинарное отношение T(M) не обладает ни свойством рефлексивности, ни свойством иррефлексивности, то оно является нерефлексивным.

Если во множестве М содержится хотя бы один элемент x, то правильная классификация не представляет сложности.

Но как быть в граничном случае, если множество М или Т– пусты? В этом случае, с точки зрения классических воззрений, бинарные отношения и являются одновременно как рефлексивными, так и иррефлексивными множествами.

Обратите внимание, для однозначности классификации свойство рефлексивности можно определять только для непустых множеств! В соответствии с этим, бинарное отношение на пустом множестве будет, является нерефлексивным. Также как нерефлексивным будет пустое бинарное отношение.

Таким образом, оба способа классификации дают один и тот же результат на всем универсуме, за исключением и .

Рассмотрим множество M={a,b,c,d}. На рис.4 приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.



рефлексивность

иррефлексивность

Рис. 4. Примеры бинарных отношений

Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары (x,у) , обратная пара (у,x) также принадлежит этому бинарному отношению, т.е. .

Классическим определением свойства симметричности является утверждение:



Прямо противоположное свойство бинарных отношений называется антисимметричностью. Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда для каждой пары различных элементов x и у пара (у, x) не принадлежит этому бинарному отношению, т.е. .

Классическим определением антисимметричности можно считать следующее [2]. Из того, что в антисимметричном бинарном отношении T(M) для любой пары пара (у,х) также принадлежитT(M), , следует, что х=у, .

Если бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричности.

В случае, когда М или Т(М) – пусты, или М содержит единственный элемент х, наше бинарное отношение одновременно является как симметричным, так и антисимметричным.

Для однозначности классификации, множество М должно содержать хотя бы два различных элемента х и у. Тогда, бинарные отношения на пустом множестве , так же как на множествах с одним элементом, является несимметричными.

Рассмотрим множество M={a,b,c,d}. На рис.5 приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.

Рис. 5. Симметричность бинарных отношений

Свойство транзитивности определяется на трех элементах множества М. Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар элементов (x,у) и (у,z), принадлежащих бинарному отношению , пара (x,z) также принадлежит этому бинарному отношению, т.е. . При графическом представлении транзитивного бинарного отношения (рис. 6) можно увидеть «спрямление» пути длины два (x, у) (у ,z), между двумя элементами, т.е. транзитивное замыкание («транзит») между x и z.

Классическое определение свойства транзитивности формулируется следующим образом: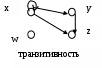

Рис. 6. Транзитивность

Бинарное отношение T(M) называется интранзитивным тогда и только тогда, когда для каждых двух пар элементов (x,у) и (у,z), принадлежащих бинарному отношению , пара (x,z) не принадлежит этому бинарному отношению, т.е. . При графическом представлении интранзитивного бинарного отношения (рис. 7) можно увидеть, что ни один имеющийся путей не обладает транзитивным замыканием!

Классическое определение свойства транзитивности формулируется следующим образом:

Рис. 7. Бинарные отношения

Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным.

Задача 4

На множестве M1= {a, b, c, d, e, f} построить бинарное отношение R, с заданными свойствами при условии, что .

Решение

Правильных решений этой задачи целое множество! Некоторые из них приведены на рис.8.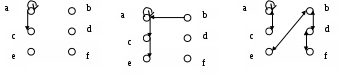

Рис. 8. Решения задачи № 4

Задача 5

О 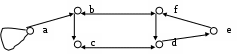пределить свойства бинарного отношения T, заданного на множестве M2= {a, b, c, d, e, f}

Решение

Данное бинарное отношение обладает свойствами:

• 
  нерефлексивности (часть вершин имеет петли, часть – нет),
  
• 
  несимметричности (есть симметричные и антисимметричные дуги),
  
• 
  интранзитивности (бинарное отношение обладает несколькими путями длины два, но, ни на один из них нет транзитивного замыкания).
  

Литература

1. 
   Новиков Ф.А. Дискретная математика для программистов. - СПб.: Питер, 2001. – 304с
   
2. 
   Горбатов В.А. Фундаментальные основы дискретной математики. - М.: Наука. Физматлит, 1999.-544с.
   
3. 
   Капитонова Ю.В. и др. Лекции по дискретной математике – СПб.: БВХ-Петербург,2004.- 624 с