                     Лекция 7 Лекция 7
7. Дисперсия диэлектрической и магнитной проницаемости.
Это важнейший вопрос о быстропеременных электромагнитных полях, частоты которых велики по сравнению с частотами, характерными для установления электрической и магнитной поляризации вещества.
7.1. Причина появления дисперсии и область частот, в которой она имеет место и при этом применима макроскопическая теория.
Полученные нами ранее связи между D, B и E, H для статических полей:
D = εο E + P (в СИ) или D = E + 4πP (в СГСЭ) и B = μο (H + J), (7.1)
остаются прежними и для переменных полей (по определению или согласно их обозначения D и H =  – J). – J).
Но! теперь P и J неоднозначно определяются значениями E и H в данный момент времени, т.к. сам процесс их установления – инерциальный. Например, пусть в какой-то момент времени t1 мы включаем электрическое (или магнитное H – все, то же самое) поле E, которое затем остается постоянным. После включения поля, заряженные частицы вещества (электроны, ядра атомов, положительно и отрицательно заряженные ионы) начинают смещаться под действием силы F = qE и = m  , где q, m и , где q, m и  – заряд, масса и приобретаемое ускорение заряженной частицы, соответственно. В результате чего, происходит процесс установления поляризации P вещества во времени (все то же самое после включения H – поворот дипольных магнитных pm, а вместе с ними и механических моментов молекул и постепенное установление во времени намагниченности вещества J). Этот процесс может иметь вид, показанный на рис.29 или рис.30: – заряд, масса и приобретаемое ускорение заряженной частицы, соответственно. В результате чего, происходит процесс установления поляризации P вещества во времени (все то же самое после включения H – поворот дипольных магнитных pm, а вместе с ними и механических моментов молекул и постепенное установление во времени намагниченности вещества J). Этот процесс может иметь вид, показанный на рис.29 или рис.30:

Рис.29. Рис.30.
Процесс установления, представленный на рис.30, соответствует ударному возбуждению собственных молекулярных или электронных колебаний, с которыми связано появление электрической или магнитной поляризации, если время затухания этих колебаний больше периода колебаний (в противном случае имеем процесс, приведенный на рис.29). Амплитуда этих колебаний мала по сравнению с окончательным значением P. (Ударное возбуждение – это, когда длительность действия силы меньше периода собственных колебаний.) С учетом сказанного за время установления поляризации P принимается промежуток времени ∆t = t2 – t1 , где t2 – соответствует моменту времени, при котором P(t2) = 0,8P или 0,9P окончательной величины поляризации (в литературе встречается по-разному, но это не принципиально). Это время установления называют временем релаксации.
Для разных случаев это время разное, например, что очевидно, чем больше масса частиц, тем больше будет время релаксации. Из последнего можно утверждать, что наиболее быстрый процесс установления электрической или магнитной поляризации в веществе является электронный (смещение электронов и поворот магнитных моментов электронов орбитальных и (в первую очередь спиновых)), т. к. они самые легкие и, следовательно, наименее инерционные. Время электронной релаксации – порядка атомных времен, равных a/υ, где a – размер атома (грубо – диаметр орбит электронов), а υ – электронные скорости (на орбитах) в атоме, которая значительно меньше скорости света в вакууме с (υ << c).
Если длительность Т включенного постоянного поля (или говорят период Т переменного (с частотой ν = 1/Т) поля Е или Н - все равно) значительно больше времени релаксации (Т>>∆t = t2 – t1 = a/υ), то установившийся момент (P или J) будет таким же (с высокой степенью точности), как и в случае статических полей. Это означает, что при ν << 1/∆t = υ/a связь между P, J, D, B и Е, Н остается той же, что и для статических полей, т. е. æ, χ, ε и μ остаются постоянными, и дисперсии нет (они не зависят от частоты ν). Если же наоборот, частота переменных полей значительно больше (можно просто больше) величины обратной времени релаксации (ν >> 1/∆t = υ/a), то указанная выше связь становится неоднозначной (это видно из рисунков – на временном участке от t1 до t2 величина P и J меняются, а Е и Н при этом, остаются постоянными). Кроме того, величины æ, χ, ε и μ становятся зависимыми от частоты переменного поля ν, т.е. имеет место дисперсия. Итак, величина υ/a является нижней частотной границей начала дисперсии (ν >> υ/a). Порядок величины этих частот зависит от рода вещества и меняется в очень широких пределах. Он может быть также совершенно различным для электрических и магнитных явлений. Так, например, в алмазе электрическая поляризация имеет электронное происхождение, и дисперсия ε начинается лишь в ультрафиолетовой области спектра. В воде же поляризация связана с ориентацией молекул с жесткими дипольными моментами, и дисперсия ε начинается при частотах ν 1011 (т.е. в сантиметровом диапазоне длин волн). Еще раньше может начинаться дисперсия μ в ферромагнитных веществах.
Переменное во времени электромагнитное поле, как вы уже знаете, необходимо является переменным также и в пространстве. При частоте ν пространственная периодичность определяется длиной волны λ = с/ν (в вакууме). Нижняя частотная граница начала дисперсии, ν = υ/a (будем так полагать), соответствует длине волны λ = с/ν = a с/υ и т. к. с/υ >> 1, то λ >> a – размеров атома и не только атомов, но и межатомных расстояний, примерно равных 10 200a (твердое тело 200a (твердое тело газ), поскольку с/υ газ), поскольку с/υ
105. При таких условиях макроскопическая теория электромагнитного поля применима (т.е. можно выбрать физически бесконечно малый объем – напомним его размеры порядка 10 00a (твердое тело 00a (твердое тело газ) << λ в пределах которого поля Е и Н можно считать постоянными). При увеличении частоты длина волны λ становится, в конце концов, сравнимой с размерами a. В таких условиях становится невозможным макроскопическое описание поля. Таким образом, определяется верхняя граница применимости макроскопической теории – λ >> a или ν << с/a . Итак, диапазон длин волн или частот, в пределах которого имеет место дисперсия и работает макроскопическая теория поля, есть: газ) << λ в пределах которого поля Е и Н можно считать постоянными). При увеличении частоты длина волны λ становится, в конце концов, сравнимой с размерами a. В таких условиях становится невозможным макроскопическое описание поля. Таким образом, определяется верхняя граница применимости макроскопической теории – λ >> a или ν << с/a . Итак, диапазон длин волн или частот, в пределах которого имеет место дисперсия и работает макроскопическая теория поля, есть:
aс/υ >> λ >> a ; υ/a <<ν << с/a (7.2)
Ниже мы предполагаем, что условие λ >> a выполнено.
7.2. Связь между D и E при наличии дисперсии.
Излагаемая ниже формальная теория в равной степени относится как к металлам, так и к диэлектрикам. Причем при частотах, соответствующих внутриатомным электронным движениям (оптические частоты) и более высоких, фактически исчезает даже количественное отличие в свойствах металлов и диэлектриков.
Формальный вид уравнений Максвелла в среде без сторонних токов и зарядов (в СГСЭ)
divD = 0, divB = 0, (7.3)
rotE = –  , rotH = , rotH =  (7.4) (7.4)
остается таким же и в произвольных переменных электромагнитных полях. Но! эти уравнения в значительной степени беспредметны до тех пор, пока не установлена связь между входящими в них величинами D, B и E, H. При рассматриваемых нами теперь больших частотах эта связь не имеет ничего общего с той, которая справедлива в статическом случае (и для квази переменных полей, когда нет дисперсии, а ε и μ соответствуют статическим полям). Нарушается даже имевшее место ранее основное свойство этой связи – однозначная зависимость D и B от значений E и H в тот же момент времени. В общем случае произвольного переменного поля значения D и B в некоторый момент времени (как и Р и J) определяются не только значениями E и H в тот же момент времени, но и зависит от значений функций E(t) и H(t) во все предыдущие моменты времени. (Это обстоятельство связано с установлением электрической и магнитной поляризации вещества, которое не успевает следовать за изменением электромагнитного поля).
В дальнейшем мы будем говорить о зависимости D от E; специфические же особенности магнитных свойств вещества будем отмечать отдельно. (Пользоваться будем системой ед. СГСЭ.)
Мы уже отметили, что связь между D и E, P (D = E + 4πP) (7.1) остается прежней и для быстропеременных полей, а Р по-прежнему имеет смысл электрического момента единицы объема вещества. В быстропеременных полях обычно имеем дело со сравнительно малыми напряженностями электрических полей, тогда связь D с E (и P и E) можно считать линейной. Наиболее общий вид линейной зависимости между D(t) и значениями E(t) во все предыдущие моменты времени может быть записана в виде интегрального соотношения
D(t) = E(t) +  (7.5) (7.5)
(выделение члена E(t) удобно, при этом второе слагаемое в правой части – сам интеграл – соответствует значению 4πP, смотри (7.1)). Здесь f(τ) – функция времени, зависящая от свойств среды. По аналогии с формулой D=εE для статических полей будем писать соотношение (7.5) в символической форме D =  E, где E, где  линейный интегральный оператор, действие которого определяется согласно (7.5) линейный интегральный оператор, действие которого определяется согласно (7.5)
 = 1 + = 1 +  . (7.6) . (7.6)
Всякое переменное во времени поле можно представить в виде совокупности монохроматических компонент (т.е. разложить в спектр Фурье), в которых зависимость всех величин от времени дается множителем е–iωt. Это разложение имеет вид:
E(t) =  , (7.7) , (7.7)
где E(ω) =   (7.8) (7.8)
Тогда для каждой спектральной компоненты E(ω)e–iωt можно записать
D(ω) = ε(ω) E(ω),
или просто для монохроматических полей связь (7.5) между D и E приобретает вид
D = ε(ω)E, (7.9)
где функция ε(ω) (крыжечку больше писать не будем) определяется как ((7.7) подставили в (7.6))
ε(ω) = 1 + 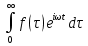 (7.10) (7.10)
Таким образом, для периодических полей может быть введено понятие о диэлектрической проницаемости как о коэффициенте пропорциональности между D и E, причем этот коэффициент зависит не только от свойств среды, но и от частоты ω поля. О зависимости ε от частоты говорят как о законе ее дисперсии.
Л 2014 Функция ε(ω), в общем случае, комплексная. Будем обозначать ее вещественную и мнимую части, как ε′ и ε′′, соответственно, тогда:
ε(ω) = ε′(ω) + i ε′′(ω). (7.11)
Если в выражении (7.10), частоту ω заменить на –ω, то получим
ε(–ω) = 1 +  = ε*(ω) , т.е. = ε*(ω) , т.е.
ε(–ω) = ε*(ω) . (7.12)
С учетом (7.11) соотношение (7.12) имеет вид:
ε′(–ω) + i ε′′(–ω) = ε*(ω) = ε′(ω) – i ε′′(ω).
Отделяя в последнем соотношении вещественную и мнимую части, получим
ε′(–ω) = ε′(ω) , ε′′(–ω) = – ε′′(ω) . (7.13)
Таким образом, ε′(ω) является четной, а ε′′(ω) – нечетной функцией частоты.
При малых (по сравнению с границей начала дисперсии, т.е. 0 ≤ ω ≤ 2πс/a) частотах функцию ε(ω) можно разложить в ряд по степеням ω. Разложение четной функции ε′(ω) содержит только члены четных степеней, а разложение нечетной функции ε′′(ω) – лишь члены нечетных степеней.
В диэлектриках – в пределе при ω → 0 функция ε(ω) стремится, очевидно, к электростатической диэлектрической проницаемости ε(0) – так здесь ее обозначим, чтобы не было путаницы. Поэтому в диэлектриках разложение ε′(ω) начинается с постоянного члена ε(0); разложение же ε′′(ω) начинается, вообще говоря (с некоторой оговоркой – поясним чуть позже) с члена, пропорционального первой степени частоты ω.
В проводниках для получения значения функции ε(ω) при малых частотах необходимо осуществить предельный переход при ω → 0 от уравнения для переменного поля в отсутствии токов проводимости
rot H = 
к уравнению для постоянного поля в проводниках
rot H =  j = j =  σE . σE .
Сравнивая между собой правые части этих уравнений видно, что в пределе при ω → 0 должно выполняться равенство
 = =  σE . (7.14) σE . (7.14)
Тогда учитывая, что для переменного поля пропорционального
e–iωt производная 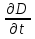 = –iωεE , получим следующее выражение для ε(ω) при малых частотах: = –iωεE , получим следующее выражение для ε(ω) при малых частотах:
ε(ω) = i 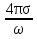 . (7.15) . (7.15)
Таким образом, в проводниках разложение функции ε(ω) начинается с мнимого члена, пропорционального 1/ω, который выражается через обычную проводимость σ по отношению к постоянным токам. Эта постоянная, однако, не имеет у металлов того электростатического смысла, которым она обладает у диэлектриков. Кроме того этот член разложения может оказаться не имеющим никакого вообще смысла, если эффекты пространственной неоднородности поля электромагнитной волны появляются раньше, чем эффекты его временной периодичности.
Для плохих проводников – имеющих достаточно низкую проводимость, или для плохих диэлектриков – имеющих достаточно высокую (как видим все относительно) проводимость величиной ε(ω) является сумма i 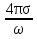 + ε , где ε = ε(0) + αω + ... + ε , где ε = ε(0) + αω + ...
7.3. Диэлектрическая проницаемость при очень высоких частотах.
Из простых физических соображений можно сразу предположить, что при ω →  функция ε(ω) должна стремиться к единице, т.к. при очень быстропеременном поле процесса поляризации, приводящего к отличию индукции D от напряженности E электрического поля не должны происходить. Установим эту зависимость. функция ε(ω) должна стремиться к единице, т.к. при очень быстропеременном поле процесса поляризации, приводящего к отличию индукции D от напряженности E электрического поля не должны происходить. Установим эту зависимость.
В соответствии с только что сказанным, мы должны положить частоту ω значительно большей частот движения всех электронов в атомах (или, по крайней мере, их большинства) данного вещества (частота движения – величина обратная соответствующему времени релаксации). При этом условии при вычислении поляризации вещества можно рассматривать электроны как свободные, пренебрегая их взаимодействием друг с другом и с ядрами атомов. (Напомним – у нас еще выполнено условие (7.2) λ >> a или эквивалентное ω/2π = ν << с/a , необходимое для использования макроскопической теории.)
При указанных условиях, расстояния υ  , проходимые электронами в течение периода волны, малы по сравнению, как с длиной волны λ, так и с размером a атома. Кроме этого при определении скорости и смещения, приобретаемым электроном в поле электромагнитной волны, последнее (поле) можно считать однородным. , проходимые электронами в течение периода волны, малы по сравнению, как с длиной волны λ, так и с размером a атома. Кроме этого при определении скорости и смещения, приобретаемым электроном в поле электромагнитной волны, последнее (поле) можно считать однородным.
Уравнение движения электрона в переменном (во времени) поле имеет вид m  = eE = eE0e–iωt , где m, e – масса и заряд электрона, а E0 –амплитуда переменного поля. Представим скорость υ движения электрона в виде υ= υ0 + = eE = eE0e–iωt , где m, e – масса и заряд электрона, а E0 –амплитуда переменного поля. Представим скорость υ движения электрона в виде υ= υ0 +  и, соответствующее им смещение r = r0 + и, соответствующее им смещение r = r0 +  , и учтем, что для реальных полей υ0 >> , и учтем, что для реальных полей υ0 >>  r0 >> r0 >>  . Тогда уравнение движения примет вид m . Тогда уравнение движения примет вид m  = eE0 e–iωt . Дважды проинтегрировав это уравнение, получим ( = eE0 e–iωt . Дважды проинтегрировав это уравнение, получим (  = =  ) )  = – eE/mω2 . Полученное выражение относится к любому электрону в атомах вещества. Поляризация вещества Р есть дипольный момент единицы его объема (Р = n<р>). Суммируя по всем электронам, находим Р = – eE/mω2 . Полученное выражение относится к любому электрону в атомах вещества. Поляризация вещества Р есть дипольный момент единицы его объема (Р = n<р>). Суммируя по всем электронам, находим Р
|
 Скачать 325.74 Kb.
Скачать 325.74 Kb. 200a (твердое тело
200a (твердое тело газ), поскольку с/υ
газ), поскольку с/υ 



 – J).
– J).  , где q, m и
, где q, m и 
 00a (твердое тело
00a (твердое тело , rotH =
, rotH =  (7.4)
(7.4) (7.5)
(7.5) E, где
E, где  . (7.6)
. (7.6) , (7.7)
, (7.7)
 (7.8)
(7.8)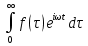 (7.10)
(7.10) = ε*(ω) , т.е.
= ε*(ω) , т.е. j =
j =  σE . (7.14)
σE . (7.14)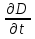 = –iωεE , получим следующее выражение для ε(ω) при малых частотах:
= –iωεE , получим следующее выражение для ε(ω) при малых частотах: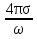 . (7.15)
. (7.15) функция ε(ω) должна стремиться к единице, т.к. при очень быстропеременном поле процесса поляризации, приводящего к отличию индукции D от напряженности E электрического поля не должны происходить. Установим эту зависимость.
функция ε(ω) должна стремиться к единице, т.к. при очень быстропеременном поле процесса поляризации, приводящего к отличию индукции D от напряженности E электрического поля не должны происходить. Установим эту зависимость. , проходимые электронами в течение периода волны, малы по сравнению, как с длиной волны λ, так и с размером a атома. Кроме этого при определении скорости и смещения, приобретаемым электроном в поле электромагнитной волны, последнее (поле) можно считать однородным.
, проходимые электронами в течение периода волны, малы по сравнению, как с длиной волны λ, так и с размером a атома. Кроме этого при определении скорости и смещения, приобретаемым электроном в поле электромагнитной волны, последнее (поле) можно считать однородным. = eE = eE0e–iωt , где m, e – масса и заряд электрона, а E0 –амплитуда переменного поля. Представим скорость υ движения электрона в виде υ= υ0 +
= eE = eE0e–iωt , где m, e – масса и заряд электрона, а E0 –амплитуда переменного поля. Представим скорость υ движения электрона в виде υ= υ0 +  и, соответствующее им смещение r = r0 +
и, соответствующее им смещение r = r0 +  , и учтем, что для реальных полей υ0 >>
, и учтем, что для реальных полей υ0 >>  = eE0 e–iωt . Дважды проинтегрировав это уравнение, получим (
= eE0 e–iωt . Дважды проинтегрировав это уравнение, получим (  )
)