урок !. Логарифмические уравнения
 Скачать 103.38 Kb. Скачать 103.38 Kb.
|
|
Тема занятия «Логарифмические уравнения» Ход занятия. I. Организационный момент. Добрый день, присаживайтесь! Давайте отметим отсутствующих. Вы, наверное, уже заметили, что сегодня у нас необычное занятие. Во-первых, на занятии присутствуют гости, во-вторых, в аудитории звучит музыка. Почему именно сегодня мы слышим её на занятии математики? Известный физик А. Эйхенвальд заметил, что «играя по клавишам современного рояля, мы играем по логарифмам». Дело в том, что ступени 12-ти звуковой гаммы частот звуковых колебаний и есть логарифмы. На предыдущем занятии мы с вами выучили определение логарифма, основные свойства логарифма, а чем же мы займемся сегодня? Преподаватель: Как вы успели заметить, на доске не записана тема сегодняшнего занятия. Вам предстоит самим определить ее. Вы видите равенства, содержащие переменную (они заранее записаны на доске):    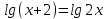 Что общего у них? Как называют эти равенства? Как вы думаете, с каким видом уравнений мы сегодня познакомимся? Обучающиеся отвечают: Эти уравнения содержат переменную под знаком логарифма и называются логарифмическими Преподаватель: Подумайте, какая тема урока будет у нас сегодня? Обучающиеся : «Логарифмические уравнения». Слайд №1 Преподаватель: правильно! Мы познакомимся с новым для вас видом уравнений – логарифмическим и способами их решения. Преподаватель: Значит какова цель нашего занятия? Слайд №2 Обучающиеся: Сегодня на уроке мы рассмотрим понятие логарифмические уравнения, узнаем способы решения, рассмотрим алгоритм решения логарифмических уравнений и как применять. Преподаватель: скажите А зачем они нужны логарифмы? Где используются? Предполагаемый ответ: Логарифмы облегчают и ускоряют вычисления. Применяются в различных областях биологии, в химии, астрономии, музыке, физики. Преподаватель: Важны ли в вашей профессиональной деятельности? (Музыку выключить) Обращаю ваше внимание, у каждого на столе лежит оценочный лист. Сегодня на уроке вы будете сами оценивать свою учебную деятельность, выполняя задания и набирая баллы. Желаю вам успеха! III Актуализация опорных знаний обучающихся. Подготовка обучающихся к активному и сознательному усвоению нового материала. Устная работа 3.1 Преподаватель: Какие знания будут нам необходимы для решения логарифмических уравнений? Слайд №3 Обучающиеся отвечают: чтобы решить логарифмические уравнения нужно знать: 1. Определение логарифма; 2. Формулы и свойства логарифмов; 3. Методы решения логарифмических уравнений. Преподаватель: Сформулируйте определение логарифма. Слайд №4 На доске плакат:
Вставьте в определение недостающие слова. Логарифмом ………………………числа b по ……………. а , а…0, а …1 называется ……………. степени, в которую нужно ……………….. основание a, чтобы получить число b. Обучающийся отвечает: Логарифмом положительного числа b по основанию Преподаватель: Давайте повторим свойства логарифма, которые мы можем использовать при решении логарифмических уравнений? Слайд №5 Слайд №6 Исправить ошибки в формулах:
Преподаватель: А теперь математическая эстафета. Слайд 7 Используя свойства и определение логарифма каждой команде предлагается вычислить логарифмы (по одному логарифму для каждой парты). Студентам дается на эстафету 5 минут. Вы находите значения логарифма в парах, а затем по очереди, передавая эстафету одна парта - другой, последний участник команды из полученных букв составляет слово, подходит ко мне и выбирает из предложенных вариантов правильное слово.
С помощью предложенной таблицы сопоставьте каждому ответу правильную букву.
Должны получиться слова: 1 команда – логарифм 2 команда – уравнение 3 команда - основание IV. Изучение нового материала (с поэтапным закреплением) слайд 8 Преподаватель: Молодцы. Прежде чем приступить к изучению логарифмических уравнений, вспомним, что значит решить уравнение? Обучающиеся: решить уравнение – означает найти множество всех его решений (корней) или доказать, что корней нет. Преподаватель: верно! При решении логарифмических уравнений пользуются свойствами логарифмов, а также свойствами логарифмической функции. Какова область определения логарифмической функции? Обучающиеся: Область определения логарифмической функции (ООФ) – множество всех положительных чисел. Преподаватель: верно! А сейчас на примере y = log2 (x – 3) назовите ООФ. (Слайд 9) Обучающиеся: x – 3>0 x >3 Преподаватель: отлично! А теперь вернемся к теме нашего занятия. Вспомните, какие методы решения уравнений вы знаете и какие из них можно применить для решения логарифмических уравнений. (Слайд10 ) Обучающиеся называют методы решения уравнений: - по определению; - преобразование уравнения по формулам; - введение новой переменной; - графический. Преподаватель: Замечательно. Но сегодня мы с вами остановимся только на некоторых из перечисленных вами методов. Преподаватель: Кто может сказать, что еще необходимо знать, чтобы решить логарифмическое уравнение? Обучающиеся отвечают: алгоритм решения. (Слайд 11) Преподаватель дописывает на доске четвертый пункт: 1. Определение логарифма; 2. Формулы и свойства логарифмов; 3. Методы решения логарифмических уравнений; 4. Алгоритм решения Преподаватель: Ребята, давайте попробуем составить алгоритм решения любого, независимо от вида и метода решения, логарифмического уравнения. На осмысление у вас есть 3 минуты. Слайд 12 Обучающиеся отвечают: Записать условия, задающие ОДЗ. Выбрать метод решения. Решить уравнение. Проверить получившиеся корни, подставив их в условия ОДЗ. При записи ответа, исключить посторонние корни. Решение простейших уравнений: (Слайд 13)Логарифмическое уравнение – это уравнение, в котором переменная содержится под знаком логарифма.Простейшими логарифмическими уравнениями будем называть уравнение вида:log a x = b, a > 0, a ¹ 1. Это уравнение решается на основании определения логарифма:если logaх = b, то x= ab. Пример 1. Решить уравнение (Слайд 14) |
| log 3(2х - 1) = log 3 27 |
| lg 2 х - 3 lg х - 4 = 0 |
| log2(x+5)=3 |
| log23x+5log3x-2=0 |
| log2(x + 3) = log216 |
5.2. Решите устно уравнения: (Слайд 16)
1.
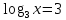 х=27
х=27 2
 х=27
х=27 3.
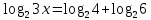 х=8
х=84.
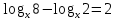 х=2
х=25.3. Самостоятельная работа.
| Вариант 1. | Вариант 2. |
| а) 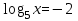 ; ;б) 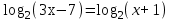 ; ;в) 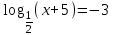 ; ;г)  д) 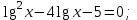 | а)  ; ;б) 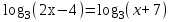 ; ;в) 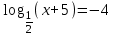 ; ;г) 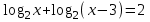 ; ;д) 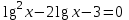 |
VI. Подведение итогов занятия Рефлексия.
Преподаватель: Давайте обобщим сведения, полученные сегодня на занятии. Какие уравнения мы сегодня решали и какие знания нам помогали их решать
VII.Домашнее задание:
1. Работа с конспектом,
2. Решить уравнения, карточки с разноуровневым дом задание. Кто желает может сделать все уровни
| 1 уровень log 3 x= 4 log 2 x= -6 logx 64 = 6 - log x64 = 3 2 log x8 + 3 = 0 | 2 уровень log 3 (2х - 1) = log 3 27 log 3 (4х+5)+log 3 (х +2) = log 3 (2х +3) log 2 х = - log 2 (6х - 1) 4 + log 3(3-х) = log 3 (135-27х) log | 3 уровень 2log 23 х - 7 log 3 х + 3 = 0 lg 2 х - 3 lg х - 4 = 0 log 2 3 х - log 3 х - 3 = 2 lоg 2 3 |
Преподаватель. И в конце занятия давайте оценим ваши впечатления. Что узнали нового? Было ли интересно, познавательно? Какие возникли трудности в усвоении нового материала? Сложно ли было вам включиться в учебный процесс?
Для этого я предлагаю заполнить «лист самоанализа деятельности обучающегося».
Лист самоанализа деятельности обучающегося
Из предложенных утверждений отметь те, с которыми вы согласны.
 Мне было интересно работать на занятии.
Мне было интересно работать на занятии. Данная тема понятна для меня.
Данная тема понятна для меня. В процессе работы у меня возникли затруднения.
В процессе работы у меня возникли затруднения. Результатом работы я доволен.
Результатом работы я доволен.Поделись впечатлениями о занятии: что понравилось или не понравилось________________________________________________________________________________________________________________________________________________________________________________________.
Рефлексия
Дайте оценку своей деятельности на уроке:
- Я работал отлично, в полную силу своих возможностей, Чувствовал себя уверенно.
- Я работал хорошо, но не в полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно.
- У меня не было желания работать. Сегодня не мой день.
С каким настроением вы уходите с урока?
Приклейте на свою оценочную карту стикер соответствующего цвета (прием «Светофор»):
- красный- тревожно, тему не понял;
- желтый- спокоен, скорее понял, чем нет:
- зеленый- понял всю тему, уверен, что смогу решить самостоятельную работу.

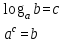
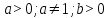
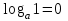
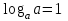
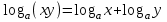
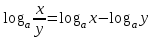
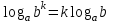

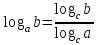
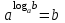
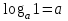
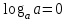


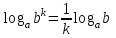


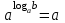


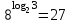
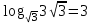

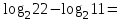


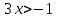 ,
,  .
.  ,
,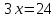 ,
,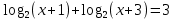
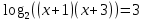 ,
,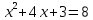 ,
,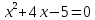 ,
, 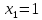 ,
, 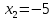 .
.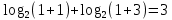 ,
, ,
,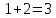 , 3=3.
, 3=3. ,
,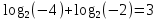 , левая часть уравнения не имеет смысла, поэтому
, левая часть уравнения не имеет смысла, поэтому 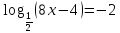 -по определению логарифма решаем
-по определению логарифма решаем