МГТУ физика 3 семестр 1 задача. Разобранные ДЗ - Электростатика. Н. Э. Баумана электростатика разобранные задачи по физике 3 семестр Редактор Fozi icq 1860 Москва, 2002 Задача
 Скачать 1.4 Mb.
|
|
МГТУ им. Н.Э. Баумана  ЭЛЕКТРОСТАТИКА Разобранные задачи по физике 3 семестр Редактор: Fozi ICQ: 1860 Москва, 2002 Задача 1.1Вариант 1Условие:Сферический конденсатор имеет радиусы внешней и внутренней обкладок R1 и R0 соответственно. Заряд конденсатора равен q. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1 и ε3=const в интервале радиусов от R1 до R0 (R1=½(R0+R)). Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора. ε2/ε1=2/1; ε3/ε1=2/1; R0/R=2/1 По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0. Решение:     Определим диэлектрическую проницаемость, как функцию радиуса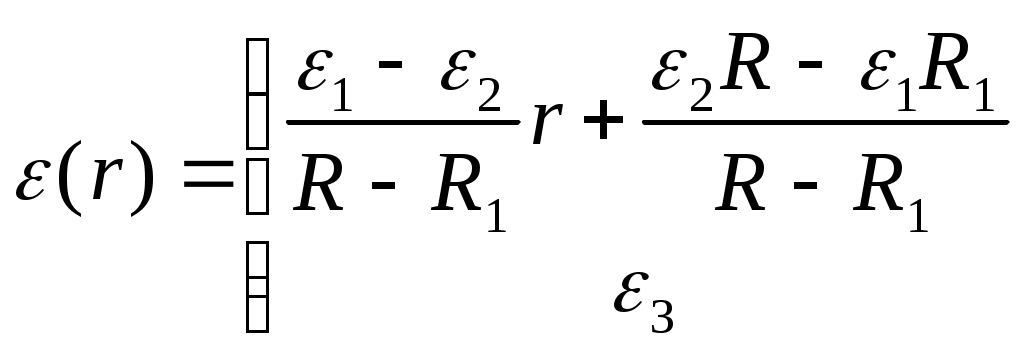 Для данного варианта  .По теореме Гаусса    и не зависит от диэлектрической проницаемости ε  .Т.к.  , то  .Поэтому  , поэтому  .Т.к.  , а  , то  ,поэтому  Определим поверхностную плотность связанных зарядов  , где  - косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности  , а для внешней поверхности  .Тогда  .Поэтому  , а  .Объёмная плотность связанных зарядов  , для полярных координат  . Для определения ёмкости вычислим напряжение на его обкладках   Поэтому   Вариант 2 |