эконометрика. На уровне значимости а 0,05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений

Название	На уровне значимости а 0,05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений
Дата	20.06.2022
Размер	160.15 Kb.
Формат файла
Имя файла	эконометрика.docx
Тип	Задача #606933

Задача 1
Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.

На уровне значимости а = 0,05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.

С надежностью p = 0,95 найти доверительные интервалы для параметров линейной регрессии.

Таблица

i		2	3	4	5	6	7	8	9	10	11	12	13	14
Xi г	32	30	36	40	41	47	56	54	60	55	61	67	69	76
Yi	20	24	28	30	31	33	34	37	38	40	41	43	45	48

Решение:

Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).

Формально критерий МНК можно записать так:

= ∑(y_i - y^*_i)² → min
Система нормальных уравнений.
a•n + b∑x = ∑y∑x + b∑x² = ∑y•x
Для наших данных система уравнений имеет вид

a + 724 b = 492

a + 40134 b = 26907

Домножим уравнение (1) системы на (-51.71), получим систему, которую решим методом алгебраического сложения.

-724a -37438.04 b = -25441.32

a + 40134 b = 26907

Получаем:

.96 b = 1465.68

Откуда b = 0.5435

Теперь найдем коэффициент «a» из уравнения (1):

a + 724 b = 492

a + 724 • 0.5435 = 492

a = 98.51= 7.0361

Получаем эмпирические коэффициенты регрессии: b = 0.5435, a = 7.0361

Уравнение регрессии (эмпирическое уравнение регрессии):= 0.5435 x + 7.0361
Таблица. Для расчета параметров регрессии построим расчетную таблицу

x	y	x²	y²	x • y
32	20	1024	400	640
30	24	900	576	720
36	28	1296	784	1008
40	30	1600	900	1200
41	31	1681	961	1271
47	33	2209	1089	1551
56	34	3136	1156	1904
54	37	2916	1369	1998
60	38	3600	1444	2280
55	40	3025	1600	2200
61	41	3721	1681	2501
67	43	4489	1849	2881
69	45	4761	2025	3105
76	48	5776	2304	3648
724	492	40134	18138	26907

Линейный коэффициент корреляции принимает значения от -1 до +1.

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

.1 xy< 0.3: слабая;

.3 xy< 0.5: умеренная;

.5 xy< 0.7: заметная;

.7 xy< 0.9: высокая;

.9 xy< 1: весьма высокая;

Линейное уравнение регрессии имеет вид y = 0.54 x + 7.04

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = 0.54 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.54.

Коэффициент a = 7.04 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y (x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 - прямая связь, иначе - обратная). В нашем примере связь прямая.

Коэффициент детерминации.

Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.

Для оценки качества параметров регрессии построим расчетную таблицу

x	y	y(x)	(y_i-y_cp)²	(y-y(x))²	\|y - y_x\|:y
32	20	24.43	229.31	19.61	0.22
30	24	23.34	124.16	0.43	0.0275
36	28	26.6	51.02	1.95	0.0499
40	30	28.78	26.45	1.5	0.0408
41	31	29.32	17.16	2.82	0.0542
47	33	32.58	4.59	0.18	0.0127
56	34	37.47	1.31	12.06	0.1
54	37	36.39	3.45	0.38	0.0166
60	38	39.65	8.16	2.71	0.0433
55	40	36.93	23.59	9.43	0.0768
61	41	40.19	34.31	0.66	0.0198
67	43	43.45	61.73	0.2	0.0105
69	45	44.54	97.16	0.21	0.0103
76	48	48.34	165.31	0.12	0.00713
724	492	492	847.71	52.26	0.69

Значимость коэффициента корреляции.

Выдвигаем гипотезы:₀: r_xy = 0, нет линейной взаимосвязи между переменными;₁: r_xy ≠ 0, есть линейная взаимосвязь между переменными;

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=12 находим t_крит:

_крит (n-m-1;α/2) = (12;0.025) = 2.179

где m = 1 - количество объясняющих переменных.

Если |t_набл| >t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).

Поскольку |t_набл| >t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим

В парной линейной регрессии t²_r = t²_b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Интервальная оценка для коэффициента корреляции (доверительный интервал).

Доверительный интервал для коэффициента корреляции.

(0.813;1)

Индивидуальные доверительные интервалы для Y при данном значении X.

(a + bx_i ± ε)

где _крит (n-m-1;α/2) = (12;0.025) = 2.179

Таблица

x_i	y = 7.04 + 0.54x_i	ε_i	y_min = y - ε_i	y_max = y + ε_i
32	24.43	5.01	19.41	29.44
30	23.34	5.08	18.26	28.42
36	26.6	4.9	21.7	31.51
40	28.78	4.82	23.96	33.59
41	29.32	4.8	24.52	34.12
47	32.58	4.73	27.86	37.31
56	37.47	4.72	32.75	42.19
54	36.39	4.71	31.67	41.1
60	39.65	4.76	34.88	44.41
55	36.93	4.72	32.21	41.64
61	40.19	4.78	35.41	44.97
67	43.45	4.89	38.56	48.34
69	44.54	4.94	39.59	49.48

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

Проверка гипотез относительно коэффициентов линейного уравнения регрессии.

) t-статистика. Критерий Стьюдента.

_крит (n-m-1;α/2) = (12;0.025) = 2.179

Поскольку 13.51 > 2.179, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 3.27 > 2.179, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Доверительный интервал для коэффициентов уравнения регрессии.

Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:

(b - t_критS_b; b + t_критS_b)

(0.54 - 2.179 • 0.0402; 0.54 + 2.179 • 0.0402)

(0.456;0.631)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

(a - t_критS_a; a + t_крит S_a)

(7.036 - 2.179 • 2.15; 7.036 + 2.179 • 2.15)

(2.344;11.728)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

F-статистика. Критерий Фишера.
где m - число факторов в модели.

Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:

. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α.

2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.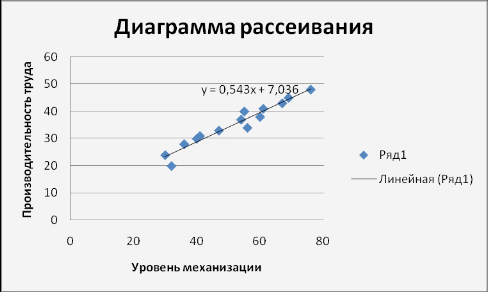

Задача 2
Исследуется зависимость производительности труда (Yi) от уровня механизации работ (Xi %) и среднего возраста работников (Xi лет) по данным 14 промышленных предприятий (i - порядковый номер предприятия). Статистические данные приведены в таблице .

Требуется:

Вычислить ковариации и составить ковариационную матрицу.

Найти оценки параметров множественной линейной регрессии и составить уравнение плоскости регрессии у = b₀+b₁x +b₂x

На уровне значимости а = 0,05 проверить гипотезу о согласии линейной множественной регрессии с результатом наблюдений.

С надежностью p = 0,95 найти доверительные интервалы для параметров множественной линейной регрессии. 2.1.
Таблица

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14
X1i	32	30	36	40	41	4	56	54	60	55	61	67	69	76
X2i	33	31	41	39	46	43	34	38	42	35	39	44	40	41
Yi	20	24	28	30	31	33	34	37	38	40	41	43	45	48

Решение:

Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (X^TX)^-1X^TY
Таблица

1	32	33
1	30	31
1	36	41
1	40	39
1	41	46
1	47	43
1	56	34
1	54	38
1	60	42
1	55	35
1	61	39
1	67	44
1	69	40
1	76	41

Матрица Y

20
24
28
30
31
33
34
37
38
40
41
43
45
48

Таблица. Матрица X^T

1	1	1	1	1	1	1	1	1	1	1	1	1	1
32	30	36	40	41	47	56	54	60	55	61	67	69	76
33	31	41	39	46	43	34	38	42	35	39	44	40	41

В матрице, (X^TX) число 14, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X^T и 1-го столбца матрицы X

Умножаем матрицы, (X^TY)
Находим обратную матрицу (X^TX)^-1

6.168	-0.0023	-0.153
-0.0023	0.000427	-0.000508
-0.153	-0.000508	0.0046

Вектор оценок коэффициентов регрессии равен

Уравнение регрессии (оценка уравнения регрессии)

= 1.74 + 0.53X₁ + 0.16X₂

Матрица парных коэффициентов корреляции R.

Число наблюдений n = 14. Число независимых переменных в модели равно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (14 х 4).

Матрица, составленная из Y и X

1	20	32	33
1	24	30	31
1	28	36	41
1	30	40	39
1	31	41	46
1	33	47	43
1	34	56	34
1	37	54	38
1	38	60	42
1	40	55	35
1	41	61	39
1	43	67	44
1	45	69	40
1	48	76	41

Транспонированная матрица.

1	1	1	1	1	1	1	1	1	1	1	1	1	1
20	24	28	30	31	33	34	37	38	40	41	43	45	48
32	30	36	40	41	47	56	54	60	55	61	67	69	76
33	31	41	39	46	43	34	38	42	35	39	44	40	41

Матрица A^TA.

14	492	724	546
492	18138	26907	19384
724	26907	40134	28533
546	19384	28533	21544

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x₁	∑x₂
∑y	∑y²	∑x₁ y	∑x₂ y
∑x₁	∑yx₁	∑x₁²	∑x₂ x₁
∑x₂	∑yx₂	∑x₁ x₂	∑x₂²

Найдем парные коэффициенты корреляции.

Признаки x и y	∑x_i	∑y_i∑x_iy_i
Для y и x₁	724	51.714	492	35.143	26907	1921.929
Для y и x₂	546	39	492	35.143	19384	1384.571
Для x₁ и x₂	546	39	724	51.714	28533	2038.071

Признаки x и y
Для y и x₁	192.347	60.551	13.869	7.781
Для y и x₂	17.857	60.551	4.226	7.781
Для x₁ и x₂	17.857	192.347	4.226	13.869

Матрица парных коэффициентов корреляции R:

-	y	x₁	x₂
y	1	0.969	0.426
x₁	0.969	1	0.362
x₂	0.426	0.362	1

Оценка дисперсии равна:

_e² = (Y - X*Y(X))^T(Y - X*Y(X)) = 46.76

Коэффициент детерминации
R² = 0.945

Коэффициент детерминации.

0.972² = 0.945

Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).

Число v = n - m - 1 называется числом степеней свободы. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.

t-статистика

_табл (n-m-1;α/2) = (11;0.025) = 2.201

(b_i - t_iS_bi; b_i + t_iS_bi)

b₀: (1.74 - 2.201 • 5.12 ; 1.74 + 2.201 • 5.12) = (-9.53;13.01)₁: (0.53 - 2.201 • 0.0426 ; 0.53 + 2.201 • 0.0426) = (0.43;0.62)₂: (0.16 - 2.201 • 0.14 ; 0.16 + 2.201 • 0.14) = (-0.15;0.47)
Задача 3
Исследуется зависимость себестоимости единицы продукции (у тыс. р.) от объема произведенной продукции (х тыс. шт.) по данным 15 предприятий (г - порядковый номер предприятия). Статистические данные приведены в таблице. Требуется:

Построить диаграмму рассеяния. Убедиться, что между себестоимостью и объемом произведенной продукции существует нелинейная связь.

Считая, что регрессия у по х представляется многочленом второй степени, найти оценки параметров параболической регрессии и составить уравнение линии регрессии.

Построить кривую регрессии и нанести ее на диаграмму рассеяния.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Xiг	2	3	4	4	5	6	6	6	7	8	9	10	12	13	14
Yi	8	10	7	6	5	5	4	3	4	5	3	2	1	1	2

С помощью средств MS Excel нанесем точки рассеивания на координатную плоскость. Анализируя, расположение точек на диаграмме, можем утверждать наличие нелинейной связи между факторами.

Составим уравнение регрессии