Дмитрий_Двойственная. Найти минимальное значение целевой функции F(X) x

• Название: Найти минимальное значение целевой функции F(X) x
• Дата: 25.07.2022
• Размер: 25.11 Kb.
• Имя файла: Дмитрий_Двойственная.docx
• Тип: Документы; #636074
• страница: 1 из 4

Найти минимальное значение целевой функции F(X) = x₁-x₂+2x₃+2 при следующих условиях-ограничений: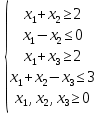

 

Для построения первого опорного плана приведем задачу к каноническому виду. Вводим в 1м неравенстве базисную переменную x₄ со знаком минус. Во 2м неравенстве базисную переменную x₅. В 3м неравенстве базисную переменную x₆ со знаком минус. В 4м неравенстве базисную переменную x₇. Получаем: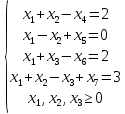

 

Введем искусственные переменные x: в 1-м равенстве вводим переменную x₈; в 3-м равенстве вводим переменную x₉; 
x₁+x₂-x₄+x₈ = 2 
x₁-x₂+x₅ = 0 
x₁+x₃-x₆+x₉ = 2 
x₁+x₂-x₃+x₇ = 3 
Для постановки задачи на минимум целевую функцию запишем так: 
F(X) = x₁-1x₂+2x₃+Mx₄+Mx₅+Mx₆+Mx₇+Mx₈+Mx₉ → min

Из уравнений выражаем искусственные переменные: 
x₈ = 2-x₁-x₂+x₄ 
x₉ = 2-x₁-x₃+x₆ 
которые подставим в целевую функцию: 
F(X) = x₁-x₂ + 2x₃ + M(2-x₁-x₂+x₄) + M(2-x₁-x₃+x₆) → min 

Получаем опорный план:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	x9
x8	2	1	1	0	-1	0	0	0	1	0
x5	0	1	-1	0	0	1	0	0	0	0
x9	2	1	0	1	0	0	-1	0	0	1
x7	3	1	1	-1	0	0	0	1	0	0
F(x)	4M	-1+2M	1+M	-2+M	-M	0	-M	0	0	0

В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент.  2я строка является ведущей:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	x9	min
x8	2	1	1	0	-1	0	0	0	1	0	2
x5	0	1	-1	0	0	1	0	0	0	0	0
x9	2	1	0	1	0	0	-1	0	0	1	2
x7	3	1	1	-1	0	0	0	1	0	0	3
F(x1)	4M	-1+2M	1+M	-2+M	-M	0	-M	0	0	0

Вместо переменной x₅ в план 1 войдет переменная x₁. Пересчитываем симплекс-таблицу относительно ведущих строки/столбца:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	x9
x8	2	0	2	0	-1	-1	0	0	1	0
x1	0	1	-1	0	0	1	0	0	0	0
x9	2	0	1	1	0	-1	-1	0	0	1
x7	3	0	2	-1	0	-1	0	1	0	0
F(x1)	4M	0	3M	-2+M	-M	1-2M	-M	0	0	0